算法
说明:这篇博文主要是对算法的总结,因此会引用大量的优质博文,也欢迎留言推荐好的算法博文
本文持续更新
文章目录
- 1 贪心算法
- 1.1 概述
- 1.2 步骤
- 1.3 举例
- 1.3.1 合并果子
- 1.3.2 剪绳子
- 1.3.3 变态跳台蛙
- 附录---贪心算法对人生的思考
- 2 递归算法
- 2.1 例题
- 2.1.1 跳蛙递归版
- 2.1.2 矩形覆盖
1 贪心算法
1.1 概述
可参考的博文—贪心算法–tattoo
可观看的视频—greedy algorithm
从上面的参考文献已经对算法有了基本的了解,现总结如下:
贪心算法: 又叫贪婪算法,在求最优解的过程中,通过将原问题分成若干子问题,对每个子问题求最优解(即选取当前状态下最好的选择(局部最优解)),并由此希望最后堆叠的结果即为原问题的最好的结果。
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解 。贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择。也就是说,不从整体最优上加以考虑,做出的只是在某种意义上的局部最优解—百度百科
1.2 步骤
- 1 将原问题分解为子问题
- 2 找出贪心策略
- 3 得到每个子问题的最优解
- 4 将所有局部最优解的集合构成原问题的一个解
1.3 举例
1.3.1 合并果子
以视频上的一个例子说明,截图可能不是很清楚

从问题描述可以看出,实际上我们只需要每次将最小的两堆果子合并即可。
- 1 将所有果子合并分成两堆果子合并----分成子问题
- 2 将果子按照数量排序,将最少的两堆果子合并,再将合并之后的果子与剩余的排序,再将合并后的果子按照数量最小的两堆合并—贪心策略
- 3 最小数量的果子合并消耗最少体力----子问题最优解
- 4 所有消耗的体力相加得到原问题最优解----子问题最优解合并成原问题最优解
算法基本如上,至于编程不是很关键。
这里我给出一个python的程序—未必很快,有更快的欢迎底下留言
def greedy(nums):
n_len = len(nums) #果子种类
sum_n = 0 #初始化总的体力消耗,初值=0
i = 0
while i < n_len-1:
nums = sorted(nums) #排序
sum_new = sum(nums[:2]) #将最少的两个种类果子相加=体力消耗
del nums[:2] #加完之后就可以删除这两种果子了
nums.append(sum_new) #将相加之后的果子加入原始果子队列中
sum_n += sum_new #计算体力消耗
i += 1
return sum_n
print(greedy([1,9,2]))
1.3.2 剪绳子
这是从牛客网看到的题,题目如下:

分析:这个问题实际上看着应该是动态规划问题,可以从动态规划上解决。当然如果从数学出发也是可以用贪心算法的。
数学分析过程:
- 回顾知道矩形周长求面积的问题,可以用求导的方法。但这题变为:
已知 x 1 + x 2 + x 3 + . . . + x m = n x_1+x_2+x_3+...+x_m=n x1+x2+x3+...+xm=n
求 x 1 × x 2 × x 3 . . . × x m x_1\times x_2\times x_3 ...\times x_m x1×x2×x3...×xm
的最大值。
从加法变为乘法,我们可以想到算术-几何平均不等式,

所以构造的算术几何平均不等式为:
x 1 + x 2 + . . . + x m m ≥ x 1 x 2 . . . x m m \frac{x_1+x_2+...+x_m}{m}\geq\sqrt[m]{x_1x_2...x_m} mx1+x2+...+xm≥mx1x2...xm
即 x 1 x 2 x 3 . . . x m ≤ ( n m ) m x_1x_2x_3...x_m\leq\left(\frac{n}{m}\right)^m x1x2x3...xm≤(mn)m
当且仅当 x 1 = x 2 = . . . = x m x_1=x_2=...=x_m x1=x2=...=xm等式成立。
也就是分成相等的段时乘积最大,那么这就简单了,可以借鉴一开始说的导数求极值的方法。
已知: x 1 + x 2 + . . . + x m = n x_1+x_2+...+x_m=n x1+x2+...+xm=n
由于每段相等,我直接假设每段长 x x x, 即 m x = n mx=n mx=n
求 x x x取何值,使得 S = x m = x n / x S=x^m=x^{n/x} S=xm=xn/x
的最大值。
这个求导采用对数求导法可以很容易得到 x = e x=e x=e(过程很简单就不写了,e是自然对数,=2.71828…)
当然,回到问题本身,由于问题要求必须是正整数,所以要么就是3要么就是2。将 x = 2 和 3 x=2和3 x=2和3带入S中,取ln,很容易得到等于3,S更大,即ln3/3>ln2/2,因此应该取3,即将绳子都剪成3的长度。
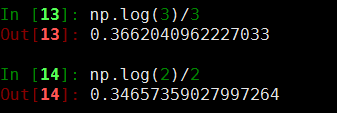
又因为m要求大于1,也就是绳子一定要剪。所以当n=2时, S S S最大值不是2,而是1;所以当n<=3时:
- n=2, S=1
- n=3, S = 1*2=2
我们上面得到的结论是在于一定可以剪成3的情况,那么当n=4呢?,显然 2 × 2 > 3 × 1 2\times2>3\times1 2×2>3×1。所以我们要优先剪成长度为3的,直到绳子小于等于4的时候,我们在将它剪为 2 × 2 2\times2 2×2.
当n>3时,容易得到,将绳子都分成长度为3的线段,除非分到无法再分,再考虑小于3的数,如2和1.
可以总结得到,当n<=3时:
- 1) n=2, S=1
- 2) n=3, S = 1*2=2
当n>3时(注意:n/3的余数无非=0,1,2): - 1) 如果n能被3整除(n%3==0),都分成长为3的线段, S = 3 n / 3 S=3^{n/3} S=3n/3
- 2)如果余数为1(n%3==1),则前面都分成3,最后一部分肯定是4,将4分成2和2两段(乘积=4),所以 S = 3 ( n − 4 ) / 3 × 4 S=3^{(n-4)/3}\times4 S=3(n−4)/3×4
- 3)如果余数为2(n%3==2),则前面分成3,后面一段一定是2,所以 S = 3 ( n − 2 ) / 3 × 2 S=3^{(n-2)/3}\times2 S=3(n−2)/3×2
class Solution:
def cutRope(self, n):
if n <=1:
print('n must great than 1...')
elif n == 2:
return 1
elif n == 3:
return 2
elif n>3:
if n%3==0:
return 3**(n/3)
elif n%3==1:
return 3**((n-4)/3)*4
elif n%3==2:
return 3**((n-2)/3)*2
print(Solution().cutRope(8))
1.3.3 变态跳台蛙
- 1) 假设只有一个台阶,则 f ( 1 ) = 1 ( f f(1)=1(f f(1)=1(f表示跳的种类数)
- 2) 假设2个台阶, f ( 2 ) = f ( 1 ) + 1 = 2 f(2)=f(1)+1=2 f(2)=f(1)+1=2,表示结果为先跳一个台阶,那么剩下1个台阶,所以跳台阶的种类数就是 f ( 1 ) f(1) f(1),或者一次跳两个台阶,只有一种,为1。
- 3)假设有3个台阶,则先跳一个台阶,剩下2个台阶,种类数为 f ( 2 ) f(2) f(2);先跳两个台阶,剩下一个,种类数为 f ( 1 ) f(1) f(1);跳3个台阶,为1。 f ( 3 ) = f ( 2 ) + f ( 1 ) + 1 = 2 + 1 + 1 = 4 f(3)=f(2)+f(1)+1=2+1+1=4 f(3)=f(2)+f(1)+1=2+1+1=4
- 4)假设有 n n n个台阶,则 f ( n ) = f ( n − 1 ) + f ( n − 2 ) + . . . + f ( 1 ) + 1 = f ( n − 1 ) + f ( n − 1 ) = 2 f ( n − 1 ) f(n)=f(n-1)+f(n-2)+...+f(1)+1=f(n-1)+f(n-1)=2f(n-1) f(n)=f(n−1)+f(n−2)+...+f(1)+1=f(n−1)+f(n−1)=2f(n−1),这就可以用递归了。或者 f ( n ) = f ( n − 1 ) + f ( n − 2 ) + . . . + f ( 1 ) + 1 = 1 + f ( 1 ) + f ( 2 ) + . . . + f ( n − 1 ) = 1 + f ( 1 ) + 2 f ( 1 ) + 2 ∗ 2 f ( 1 ) + . . . + 2 ( n − 2 ) f ( 1 ) = 1 + 2 0 + 2 1 + 2 2 + 2 3 + . . . + 2 ( n − 2 ) = 2 ( n − 1 ) f(n)=f(n-1)+f(n-2)+...+f(1)+1=1+f(1)+f(2)+...+f(n-1)=1+f(1)+2f(1)+2*2f(1)+...+2^{(n-2)}f(1)=1+2^0+2^1+2^2+2^3+...+2^{(n-2)}=2^{(n-1)} f(n)=f(n−1)+f(n−2)+...+f(1)+1=1+f(1)+f(2)+...+f(n−1)=1+f(1)+2f(1)+2∗2f(1)+...+2(n−2)f(1)=1+20+21+22+23+...+2(n−2)=2(n−1),不需要递归,且直接包括了 n = 1 n=1 n=1的情况。
不用递归
class Solution:
def jumpFloorII(self, n):
return 2**(n-1) #or pow(2,n-1)
Solution().jumpFloorII(3)
用递归
class Solution1:
def jumpFloorII(self, n):
if n == 1:
return 1
else:
return 2*self.jumpFloorII(n-1)
print(Solution1().jumpFloorII(3))
在计算量大的时候,显然不用递归要快很多
附录—贪心算法对人生的思考
这是附加的一个小节,截取了视频上的一段话。

即:我们无法做出使得未来最好的选择,但我们可以做出目前看来最好的选择,这个选择对于我们未来人生来说可能不是整体最优的,但确是局部最好的。
2 递归算法
关于递归,在数据结构与算法一书(Michael T.Goodrich著,张晓译)的第四章有非常详细的介绍。
在笔者一个对python很全的介绍中也提到了递归(第七部分第三节),这里主要使用例子来说明。
上一节的贪心算法 1.1.3跳蛙问题也可以使用递归, 现在进一步改进跳蛙问题
2.1 例题
2.1.1 跳蛙递归版
问题描述为

所以最大只能一次性跳2级,参考我们上面1.1.3节的介绍,很容易就可以得到如下结论
- 1) n = 1 , f ( 1 ) = 1 n=1, f(1) = 1 n=1,f(1)=1
- 2) n = 2 , f ( 2 ) = 2 n=2, f(2)=2 n=2,f(2)=2
- 3) n > = 3 , f ( n ) = f ( n − 1 ) + f ( n − 2 ) n>=3, f(n)=f(n-1)+f(n-2) n>=3,f(n)=f(n−1)+f(n−2)
这个由来很容易就不推导了。
现在我们首先想到的是递归,很容易编程如下:
class Solution:
def jumpFloorII(self, n):
if n == 1:
return 1
elif n == 2:
return 2
else:
return Solution().jumpFloorII(n-1)+Solution().jumpFloorII(n-2)
print(Solution().jumpFloorII(4))

但是这个算法很慢,因为 f ( n − 1 ) 和 f ( n − 2 ) f(n-1)和f(n-2) f(n−1)和f(n−2)是独立计算的,这就使得有很多重复的部分(比如 f ( n − 1 ) = f ( n − 2 ) + f ( n − 3 ) f(n-1)=f(n-2)+f(n-3) f(n−1)=f(n−2)+f(n−3),这里又计算了一遍f(n-2))
递归实际上是倒过来算的,从大往小推导。一个比较好的方法是顺着看,那么上面实际上是斐波那契数列,我们可以使用迭代来求解。
class Solution2:
def jumpFloor(self,n):
if n == 1:
return 1
elif n == 2:
return 2
else:
f1 = 1
f2 = 2
for i in range(3,n+1):
temp = f1+f2
f1 = f2
f2 = temp
return temp
print(Solution2().jumpFloor(4))
这速度就提高了很多了,(但是已经不是递归算法了,而是迭代)
当然,上面的最后赋值那部分并不一定要有第三者temp,也可以改为:
else:
f1 = 1
f2 = 2
for i in range(3,n+1):
f2,f1 = f1+f2,f2
return f2
此外,上面提到的那本书,给了一个斐波那契数列好的递归方法,(实际上跟上面的迭代一样的),python代码如下;
class Solution2:
def jumpFloor(self,n):
if n <= 1:
return (n,1) #1表示定义f(0)=1
else:
(a,b) = self.jumpFloor(n-1)
return (a+b,a)
print(Solution2().jumpFloor(8)[0]) #0表示只要a+b的结果,即最后的结果
上面之所以定义 f ( 0 ) = 1 f(0)=1 f(0)=1是因为 f ( 2 ) = f ( 2 − 1 ) + f ( 2 − 2 ) = f ( 1 ) + f ( 0 ) f(2)=f(2-1)+f(2-2)=f(1)+f(0) f(2)=f(2−1)+f(2−2)=f(1)+f(0),实际上 f ( 0 ) f(0) f(0)表示一次跳了两个台阶,所以后面剩下0个台阶,这是一种方法,算1.
至于上面的程序解释,可以参考提到的书本,或者自己理解一下,也不难。
2.1.2 矩形覆盖
- 1)n=0,不需要任何小矩形,方式为0个(也可以说是无穷个,有争议,不过答案是0,就按照答案来吧)
- 2)n=1, 一种方式, f ( 1 ) = 1 f(1)=1 f(1)=1
- 3)n=2, f ( 2 ) = f ( 2 − 1 ) + f ( 2 − 1 ) = f ( 1 ) + f ( 1 ) f(2)=f(2-1)+f(2-1)=f(1)+f(1) f(2)=f(2−1)+f(2−1)=f(1)+f(1),表示横着放一个1*2的小矩形,那么还剩一个为1*2的空位,所以是 f ( 2 − 1 ) = f ( 1 ) f(2-1)=f(1) f(2−1)=f(1);竖着放,也是一样的,故 f ( 2 ) = f ( 1 ) + f ( 1 ) f(2)=f(1)+f(1) f(2)=f(1)+f(1)
- 4)n=3, 横着放,要使得1*2铺满2*n的矩形,放完一个之后,还剩 f ( 3 − 2 ) = f ( 1 ) f(3-2)=f(1) f(3−2)=f(1)种方式,这里需要注意的是,一旦横着放了一个之后,那么它下面的1*2的那个空位也没法改动的,相当于那个位置是固定了,所以是-2;竖着放,放完之后还剩 f ( 3 − 1 ) = f ( 2 ) f(3-1)=f(2) f(3−1)=f(2)
- 5)n=n,很容易归纳出是 f ( n ) = f ( n − 1 ) + f ( n − 2 ) f(n)=f(n-1)+f(n-2) f(n)=f(n−1)+f(n−2),所以是斐波那契数列,代码跟上面一节基本完全相同,
迭代法
class Solution:
def rectCover(self, n):
# write code here
if n == 0:
return 0
if n == 1:
return 1
else:
f0 = 1
f1 = 1
for i in range(2,n+1):
f1,f0 = f0+f1,f1
return f1
递归法:
class Solution:
def rectCover(self, n):
# write code here
if n == 0:
return 0
if n == 1:
return 1
if n == 2:
return 2
else:
return Solution().rectCover(n-1)+Solution().rectCover(n-2)
递归改进版
class Solution:
def rectCover(self, n):
# write code here
if n <= 1:
return (n,1)
else:
(a,b) = Solution().rectCover(n-1)
return (a+b,a)
Solution().rectCover(3)[0]
但这个答案没法在牛客上测,因为我们需要找的是第一个输出,即a+b的那个,所以需要先实例化,但是牛客上只需要给函数。