CORDIC算法详解(六)-CORDIC 算法的硬件实现
CORDIC算法详解(六)- CORDIC 算法的硬件实现
文章目录
- CORDIC算法详解(六)- CORDIC 算法的硬件实现
- 6 CORDIC 算法的硬件实现
- 6.1 CORDIC 算法的硬件相关介绍
- 6.2 CORDIC 算法的硬件实现(圆周系统)-Verilog版
- 6.2.1 源码
- 6.2.2 仿真代码TB
- 6.2.3 流程总结
- 6.2.4 仿真过程注意事项
- 6.2.4.1 显示模拟波形(即sin/cos波形)需要怎么设置modelsim
- 6.2.4.2 仿真时间
- 6.2.5 仿真结果
- 6.2.6 工程源码
- 6.3 CORDIC 算法的硬件实现(圆周系统)- 基于System Generator
网上有很多类似的介绍,但是本文会结合实例进行介绍,尽量以最简单的语言进行解析。
CORDIC ( Coordinate Rotation Digital Computer ) 是坐标旋转数字计算机算法的简称,
由 Vloder• 于 1959 年在设计美国航空导航控制系统的过程中首先提出[1], 主要用于解决导航系统中三角函数、 反三角函数和开方等运算的实时计算问题。 1971 年, Walther 将圆周系统、 线性系统和双曲系统统一到一个 CORDIC 迭代方程里 , 从而提出了一种统一的CORDIC 算法形式[2]。
CORDIC 算法应用广泛, 如离散傅里叶变换 、 离散余弦变换、 离散 Hartley 变换、Chirp-Z 变换、 各种滤波以及矩阵的奇异值分解中都可应用 CORDIC 算法。 从广义上讲,CORDIC 算法提供了一种数学计算的逼近方法。 由于它最终可分解为一系列的加减和移位操作, 故非常适合硬件实现。 例如, 在工程领域可采用 CORDIC 算法实现直接数字频率合成器。 本节在阐述 CORDIC 算法三种旋转模式的基础上, 介绍了利用 CORDIC 算法计算三角函数、 反三角函数和复数求模等相关理论。 以此为依据, 阐述了基于 FPGA 的 CORDIC 算法的设计与实现及其工程应用。
整个系列分别从圆周系统、 线性系统和双曲系统及硬件实现进行分析,如下:
CORDIC算法详解(一)- CORDIC 算法之圆周系统之旋转模式( Rotation Mode )
CORDIC算法详解(二)- CORDIC 算法之圆周系统之向量模式(Vectoring Mode)
CORDIC算法详解(三)- CORDIC 算法之线性系统及其数学应用
CORDIC算法详解(四)- CORDIC 算法之双曲系统及其数学应用
CORDIC算法详解(五)- 统一的 CORDIC 算法形式
CORDIC算法详解(六)- CORDIC 算法的硬件实现
其中第五篇及第六篇后会放出相关参考资料及源码。
6 CORDIC 算法的硬件实现
6.1 CORDIC 算法的硬件相关介绍
考虑到硬件架构的一致性, 这里以圆周系统为例说明。 由式 (3.103 ) 和式 3.110 ) 所示的迭代方程可得出 CORDIC 算法的基本处理单元硬件架构, 如图 3.93 所示。 如果只是利用向量模式求取幅度, 图中的虚线部分结构是不需要的。
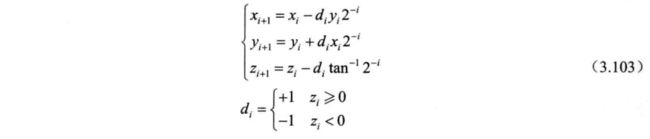
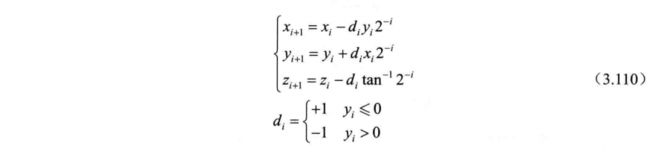
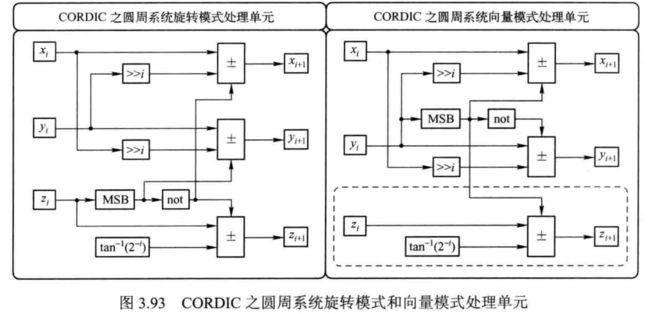
从图 3.93 中不难看出, 基本处理单元由三个加法器和一个 LUT (储存角度), 外加两个移位操作构成。 这正是 CORDIC 算法的优势。 由于每次迭代所用到的处理单元基本结构是一致的, 只是移位量和存储角度不同, 据此可得三种 CORDIC 算法硬件实现架构, 即串行结构、 并行结构和并行流水结构, 三种架构的大体框图如图 3.94 所示。 从图 3.94 中可以看出, 串行结构占用的资源最少, 这缘于对 CORDIC 处理单元的分时复用, 也正因此使得控制单元设计略显复杂, 时序控制较为烦琐, 系统处理速度较低。 并行结构是对串行结构的扩展, 对每次迭代赋予了独立的 CORDIC 处理单元, 从而无须控制电路, 只需移位、 加减操作。 这是与串行结构中 CORDIC 处理单元最大的不同。 显然, 相比于串行结构, 并行结构消耗的资源显著增加。 为了提高系统处理速度, 对并行结构添加流水寄存器, 这即为并行流水结构。 它有效地缩短了关键路径, 使得关键路径的长度由并行结构的 N 个 CORDIC 处理单 元 变 为 1 个 CORDIC 处理单元。 因此, 并行流水结构具有最快的处理速度, 而这是以消耗更多的资源换取的。

串行结构具体细节如图 3.95 所示。 图中 sgn(yi) 和 sgn(zi)分别表示yi和zi的符号位即最高位, 根据工作模式( 旋转模式还是向量模式) 的不同, 选择其中之一赋给di( 这里di为 1或者 0)。 加法器则根据di确定工作模式( 加法操作还是减法操作)。 “>> i ” 表示对输入数据右移i位, i 由 control 模块控制。 ROM 中存放的数据为每次迭代时的旋转角度tand-12-i ,可以用角度表示也可以用弧度表示, 统一即可。 串行结构的设计难点在于控制路径。 以 16次迭代为例, 即i= 0,1,2,…,15 , 设计一个模 16 的计数器 cnt 计数值由 0 至 15, 通过对计数值译码产生图中的 sel 信号, 即 cnt>0 时 sel 为 1, 否则为 0。 同时, 该计数值还可对移位量进行动态调整, 如图 3.96 所示。 此外, 该计数值还可以作为 ROM 的读地址。
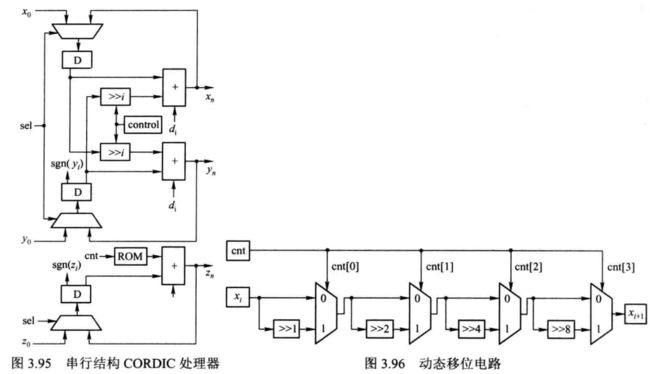
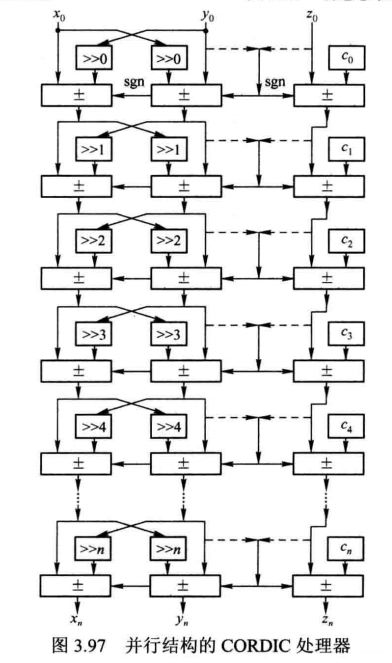
并行结构如 3.97 所示, 这里将旋转模式和向量模式的架构统一起来, 两者的区别只是在于图 3.97 中加法器的控制端。 旋转模式加法器的控制端来自于 zi 的符号位, 向量模式则来自于yi的符号位。 并行流水结构则是在并行结构的基础上对每级 CORDIC 处理单元的输出添加流水寄存器, 从而缩短关键路径, 提高系统处理速度。
6.2 CORDIC 算法的硬件实现(圆周系统)-Verilog版
参考文献:
基于FPGA的Cordic算法实现 https://www.cnblogs.com/ninghechuan/p/8681006.html?utm_source=tuicool&utm
Cordic算法——verilog实现 http://www.cnblogs.com/rouwawa/p/7102173.html
基于FPGA的cordic算法的verilog初步实现 https://www.cnblogs.com/sepeng/p/5819586.html
基于FPGA的CORDIC算法实现——Verilog版 https://blog.csdn.net/qq_39210023/article/details/77456031#comments
先上源码,后面会将整个工程奉上:
开发环境:Vivado2018+modelsim10.5c
搭建仿真环境看这里:https://blog.csdn.net/Pieces_thinking/article/details/83587695
6.2.1 源码
module Cordic_Test
(
CLK_50M,RST_N,
Phase,
Sin,Cos,Error
);
input CLK_50M;
input RST_N;
input [31:0] Phase;
output [31:0] Sin;
output [31:0] Cos;
output [31:0] Error;
`define rot0 32'd2949120 //45度*2^16
`define rot1 32'd1740992 //26.5651度*2^16
`define rot2 32'd919872 //14.0362度*2^16
`define rot3 32'd466944 //7.1250度*2^16
`define rot4 32'd234368 //3.5763度*2^16
`define rot5 32'd117312 //1.7899度*2^16
`define rot6 32'd58688 //0.8952度*2^16
`define rot7 32'd29312 //0.4476度*2^16
`define rot8 32'd14656 //0.2238度*2^16
`define rot9 32'd7360 //0.1119度*2^16
`define rot10 32'd3648 //0.0560度*2^16
`define rot11 32'd1856 //0.0280度*2^16
`define rot12 32'd896 //0.0140度*2^16
`define rot13 32'd448 //0.0070度*2^16
`define rot14 32'd256 //0.0035度*2^16
`define rot15 32'd128 //0.0018度*2^16
parameter Pipeline = 16;
parameter K = 32'h09b74; //K=0.607253*2^16,32'h09b74,
reg signed [31:0] Sin;
reg signed [31:0] Cos;
reg signed [31:0] Error;
reg signed [31:0] x0=0,y0=0,z0=0;
reg signed [31:0] x1=0,y1=0,z1=0;
reg signed [31:0] x2=0,y2=0,z2=0;
reg signed [31:0] x3=0,y3=0,z3=0;
reg signed [31:0] x4=0,y4=0,z4=0;
reg signed [31:0] x5=0,y5=0,z5=0;
reg signed [31:0] x6=0,y6=0,z6=0;
reg signed [31:0] x7=0,y7=0,z7=0;
reg signed [31:0] x8=0,y8=0,z8=0;
reg signed [31:0] x9=0,y9=0,z9=0;
reg signed [31:0] x10=0,y10=0,z10=0;
reg signed [31:0] x11=0,y11=0,z11=0;
reg signed [31:0] x12=0,y12=0,z12=0;
reg signed [31:0] x13=0,y13=0,z13=0;
reg signed [31:0] x14=0,y14=0,z14=0;
reg signed [31:0] x15=0,y15=0,z15=0;
reg signed [31:0] x16=0,y16=0,z16=0;
reg [ 1:0] Quadrant [Pipeline:0];
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x0 <= 1'b0;
y0 <= 1'b0;
z0 <= 1'b0;
end
else
begin
x0 <= K;
y0 <= 32'd0;
z0 <= Phase[15:0] << 16;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x1 <= 1'b0;
y1 <= 1'b0;
z1 <= 1'b0;
end
else if(z0[31])
begin
x1 <= x0 + y0;
y1 <= y0 - x0;
z1 <= z0 + `rot0;
end
else
begin
x1 <= x0 - y0;
y1 <= y0 + x0;
z1 <= z0 - `rot0;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x2 <= 1'b0;
y2 <= 1'b0;
z2 <= 1'b0;
end
else if(z1[31])
begin
x2 <= x1 + (y1 >>> 1);
y2 <= y1 - (x1 >>> 1);
z2 <= z1 + `rot1;
end
else
begin
x2 <= x1 - (y1 >>> 1);
y2 <= y1 + (x1 >>> 1);
z2 <= z1 - `rot1;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x3 <= 1'b0;
y3 <= 1'b0;
z3 <= 1'b0;
end
else if(z2[31])
begin
x3 <= x2 + (y2 >>> 2);
y3 <= y2 - (x2 >>> 2);
z3 <= z2 + `rot2;
end
else
begin
x3 <= x2 - (y2 >>> 2);
y3 <= y2 + (x2 >>> 2);
z3 <= z2 - `rot2;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x4 <= 1'b0;
y4 <= 1'b0;
z4 <= 1'b0;
end
else if(z3[31])
begin
x4 <= x3 + (y3 >>> 3);
y4 <= y3 - (x3 >>> 3);
z4 <= z3 + `rot3;
end
else
begin
x4 <= x3 - (y3 >>> 3);
y4 <= y3 + (x3 >>> 3);
z4 <= z3 - `rot3;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x5 <= 1'b0;
y5 <= 1'b0;
z5 <= 1'b0;
end
else if(z4[31])
begin
x5 <= x4 + (y4 >>> 4);
y5 <= y4 - (x4 >>> 4);
z5 <= z4 + `rot4;
end
else
begin
x5 <= x4 - (y4 >>> 4);
y5 <= y4 + (x4 >>> 4);
z5 <= z4 - `rot4;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x6 <= 1'b0;
y6 <= 1'b0;
z6 <= 1'b0;
end
else if(z5[31])
begin
x6 <= x5 + (y5 >>> 5);
y6 <= y5 - (x5 >>> 5);
z6 <= z5 + `rot5;
end
else
begin
x6 <= x5 - (y5 >>> 5);
y6 <= y5 + (x5 >>> 5);
z6 <= z5 - `rot5;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x7 <= 1'b0;
y7 <= 1'b0;
z7 <= 1'b0;
end
else if(z6[31])
begin
x7 <= x6 + (y6 >>> 6);
y7 <= y6 - (x6 >>> 6);
z7 <= z6 + `rot6;
end
else
begin
x7 <= x6 - (y6 >>> 6);
y7 <= y6 + (x6 >>> 6);
z7 <= z6 - `rot6;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x8 <= 1'b0;
y8 <= 1'b0;
z8 <= 1'b0;
end
else if(z7[31])
begin
x8 <= x7 + (y7 >>> 7);
y8 <= y7 - (x7 >>> 7);
z8 <= z7 + `rot7;
end
else
begin
x8 <= x7 - (y7 >>> 7);
y8 <= y7 + (x7 >>> 7);
z8 <= z7 - `rot7;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x9 <= 1'b0;
y9 <= 1'b0;
z9 <= 1'b0;
end
else if(z8[31])
begin
x9 <= x8 + (y8 >>> 8);
y9 <= y8 - (x8 >>> 8);
z9 <= z8 + `rot8;
end
else
begin
x9 <= x8 - (y8 >>> 8);
y9 <= y8 + (x8 >>> 8);
z9 <= z8 - `rot8;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x10 <= 1'b0;
y10 <= 1'b0;
z10 <= 1'b0;
end
else if(z9[31])
begin
x10 <= x9 + (y9 >>> 9);
y10 <= y9 - (x9 >>> 9);
z10 <= z9 + `rot9;
end
else
begin
x10 <= x9 - (y9 >>> 9);
y10 <= y9 + (x9 >>> 9);
z10 <= z9 - `rot9;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x11 <= 1'b0;
y11 <= 1'b0;
z11 <= 1'b0;
end
else if(z10[31])
begin
x11 <= x10 + (y10 >>> 10);
y11 <= y10 - (x10 >>> 10);
z11 <= z10 + `rot10;
end
else
begin
x11 <= x10 - (y10 >>> 10);
y11 <= y10 + (x10 >>> 10);
z11 <= z10 - `rot10;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x12 <= 1'b0;
y12 <= 1'b0;
z12 <= 1'b0;
end
else if(z11[31])
begin
x12 <= x11 + (y11 >>> 11);
y12 <= y11 - (x11 >>> 11);
z12 <= z11 + `rot11;
end
else
begin
x12 <= x11 - (y11 >>> 11);
y12 <= y11 + (x11 >>> 11);
z12 <= z11 - `rot11;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x13 <= 1'b0;
y13 <= 1'b0;
z13 <= 1'b0;
end
else if(z12[31])
begin
x13 <= x12 + (y12 >>> 12);
y13 <= y12 - (x12 >>> 12);
z13 <= z12 + `rot12;
end
else
begin
x13 <= x12 - (y12 >>> 12);
y13 <= y12 + (x12 >>> 12);
z13 <= z12 - `rot12;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x14 <= 1'b0;
y14 <= 1'b0;
z14 <= 1'b0;
end
else if(z13[31])
begin
x14 <= x13 + (y13 >>> 13);
y14 <= y13 - (x13 >>> 13);
z14 <= z13 + `rot13;
end
else
begin
x14 <= x13 - (y13 >>> 13);
y14 <= y13 + (x13 >>> 13);
z14 <= z13 - `rot13;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x15 <= 1'b0;
y15 <= 1'b0;
z15 <= 1'b0;
end
else if(z14[31])
begin
x15 <= x14 + (y14 >>> 14);
y15 <= y14 - (x14 >>> 14);
z15 <= z14 + `rot14;
end
else
begin
x15 <= x14 - (y14 >>> 14);
y15 <= y14 + (x14 >>> 14);
z15 <= z14 - `rot14;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
x16 <= 1'b0;
y16 <= 1'b0;
z16 <= 1'b0;
end
else if(z15[31])
begin
x16 <= x15 + (y15 >>> 15);
y16 <= y15 - (x15 >>> 15);
z16 <= z15 + `rot15;
end
else
begin
x16 <= x15 - (y15 >>> 15);
y16 <= y15 + (x15 >>> 15);
z16 <= z15 - `rot15;
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
Quadrant[0] <= 1'b0;
Quadrant[1] <= 1'b0;
Quadrant[2] <= 1'b0;
Quadrant[3] <= 1'b0;
Quadrant[4] <= 1'b0;
Quadrant[5] <= 1'b0;
Quadrant[6] <= 1'b0;
Quadrant[7] <= 1'b0;
Quadrant[8] <= 1'b0;
Quadrant[9] <= 1'b0;
Quadrant[10] <= 1'b0;
Quadrant[11] <= 1'b0;
Quadrant[12] <= 1'b0;
Quadrant[13] <= 1'b0;
Quadrant[14] <= 1'b0;
Quadrant[15] <= 1'b0;
Quadrant[16] <= 1'b0;
end
else
begin
Quadrant[0] <= Phase[17:16];
Quadrant[1] <= Quadrant[0];
Quadrant[2] <= Quadrant[1];
Quadrant[3] <= Quadrant[2];
Quadrant[4] <= Quadrant[3];
Quadrant[5] <= Quadrant[4];
Quadrant[6] <= Quadrant[5];
Quadrant[7] <= Quadrant[6];
Quadrant[8] <= Quadrant[7];
Quadrant[9] <= Quadrant[8];
Quadrant[10] <= Quadrant[9];
Quadrant[11] <= Quadrant[10];
Quadrant[12] <= Quadrant[11];
Quadrant[13] <= Quadrant[12];
Quadrant[14] <= Quadrant[13];
Quadrant[15] <= Quadrant[14];
Quadrant[16] <= Quadrant[15];
end
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
begin
Cos <= 1'b0;
Sin <= 1'b0;
Error <= 1'b0;
end
else
begin
Error <= z16;
case(Quadrant[16])
2'b00: //if the Phase is in first Quadrant,the Sin(X)=Sin(A),Cos(X)=Cos(A)
begin
Cos <= x16;
Sin <= y16;
end
2'b01: //if the Phase is in second Quadrant,the Sin(X)=Sin(A+90)=CosA,Cos(X)=Cos(A+90)=-SinA
begin
Cos <= ~(y16) + 1'b1;//-Sin
Sin <= x16;//Cos
end
2'b10: //if the Phase is in third Quadrant,the Sin(X)=Sin(A+180)=-SinA,Cos(X)=Cos(A+180)=-CosA
begin
Cos <= ~(x16) + 1'b1;//-Cos
Sin <= ~(y16) + 1'b1;//-Sin
end
2'b11: //if the Phase is in forth Quadrant,the Sin(X)=Sin(A+270)=-CosA,Cos(X)=Cos(A+270)=SinA
begin
Cos <= y16;//Sin
Sin <= ~(x16) + 1'b1;//-Cos
end
endcase
end
end
endmodule
6.2.2 仿真代码TB
`timescale 1 ps/ 1 ps
module Cordic_Test_tb;
// Inputs
reg CLK_50M;
reg RST_N;
reg [15:0] cnt;
reg [15:0] cnt_n;
reg [31:0] Phase;
reg [31:0] Phase_n;
wire [31:0] Sin;
wire [31:0] Cos;
wire [31:0] Error;
// Instantiate the Unit Under Test (UUT)
Cordic_Test uut
(
.CLK_50M (CLK_50M ),
.RST_N (RST_N ),
.Phase (Phase ),
.Sin (Sin ),
.Cos (Cos ),
.Error (Error )
);
initial
begin
#0 CLK_50M = 1'b0;
#10000 RST_N = 1'b0;
#10000 RST_N = 1'b1;
#10000000 $stop;
end
always #10000
begin
CLK_50M = ~CLK_50M;
end
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
cnt <= 1'b0;
else
cnt <= cnt_n;
end
always @ (*)
begin
if(cnt == 16'd359)
cnt_n = 1'b0;
else
cnt_n = cnt + 1'b1;
end
//生成相位0-359度,Phase[17:16]为相位的象限,Phase[15:10]为相位的值
always @ (posedge CLK_50M or negedge RST_N)
begin
if(!RST_N)
Phase <= 1'b0;
else
Phase <= Phase_n;
end
always @ (*)
begin
if(cnt <= 16'd90)
Phase_n = cnt;
else if(cnt > 16'd90 && cnt <= 16'd180)
Phase_n = {2'b01,cnt - 16'd90};
else if(cnt > 16'd180 && cnt <= 16'd270)
Phase_n = {2'b10,cnt - 16'd180};
else if(cnt > 16'd270)
Phase_n = {2'b11,cnt - 16'd270};
end
endmodule
6.2.3 流程总结
简单总结下流程,Cordic算法旋转模式使用Verilog HDL的实现流程
- (1) 确定迭代次数,将每次迭代的角度计算出来,预先定义为参数,为了避免浮点运算,将角度值向左移位16位,取整数部分。
- (2)
根据迭代公式进行迭代计算,本设计取16次迭代,当迭代次数越大时,1/∏cosθi会趋向于一个确定值。如果对结果精度要求更高,可以设置更高的迭代次数,根据迭代次数,可以将伸缩因子KN = 1/∏cosθi计算出来。同样将其左移16位。 - (3) 设置x0 = ∏cosθi,y0 = 0,则求出x16 = cosθ,y16 = sinθ。
这里需要注意的是,我们在进行迭代运算的时候,将2^-i变成移位运算,对于正余弦来说是有正负的,所以在一开始定义的时候,就应该定义成有符号数,Verilog中也可以定义有符号数,最高位表示符号位。
迭代寄存器定义为有符号数,那么我们移位运算就不能用>>逻辑右移<<逻辑左移或来移位了,而是用>>>算术右移和<<<算术左移。逻辑左移也就相当于算数左移,右边统一添0 ,逻辑右移,左边统一添0 ,算数右移,左边添加的数和符号有关。
例如1010_1010, []是添加的位
逻辑左移一位:0101_010[0]
算数左移一位:0101_010[0]
逻辑右移一位:[0]101_0101
算数右移一位:[1]101_0101
迭代运算采用16级流水线,进行运算,最终需要判断输出的正余弦值在哪个象限,前面讲旋转角度θ的范围为[-99.7,99.7],不在这个范围我们要进行三角运算使其满足这个范围,当输入的角度小于90度即可进行计算,当输入角度大于90度小于180度,将输入角度减去90度并设定当前角度处于第二象限,然后进行计算,当输入角度大于180度小于270度,将输入的角度减去180度设置当前角度处于第三象限,进行计算,当输入的角度大于270度,减去270设置当前角度处于第四象限,进行计算。象限的设定通过quarant寄存器实现。
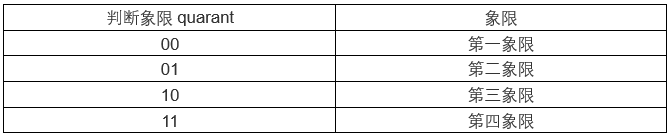
如果角度在第一象限,sin(x) = sin(a),cos(x) = sin(a)最后的结果x16 = cosθ, y16 = sinθ,这里我想起了那句口诀,一全正,二正弦,三正切,四余弦
如果角度在第二象限,sin(x) = sin(a+90) = cos(a),cos(x) = cos(a+90) = -sin(a)
如果角度在第三象限,sin(x) = sin(a+180) = -sin(a),cos(x) = cos(a+180) = -cos(a)
如果角度在第四象限,sin(x) = sin(a+270) = cos(a),cos(x) = cos(a+270) = -sin(a)
对于正数,我们直接赋值输出,负数,这里使用有符号数表示,将其取反加1即可。
6.2.4 仿真过程注意事项
6.2.4.1 显示模拟波形(即sin/cos波形)需要怎么设置modelsim
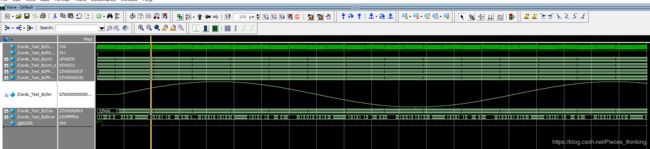
从Vivado启动modelsim后,modelsim会自动进行仿真,并显示wave窗口,初始可能如下图所示:

如果要将这个信号在modelsim中显示为正弦波图形,需要进行下面设置:
- 1、选择sin/cos信号,右击—->Radix—->Symbolic
- 2、选择sin/cos信号,右击—->Format—->Analog(automatic)
6.2.4.2 仿真时间
modelsim的仿真时间由TB里图中这个语句进行控制:
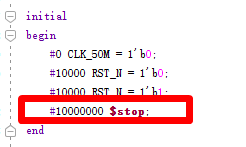
如果显示的波形不完整或者时间不够,不需要重新修改TB文件,直接点击主界面图中位置
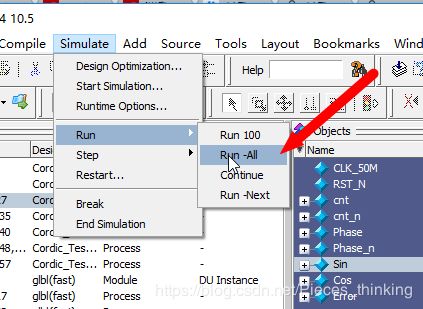
就可以一直进行仿真了
6.2.5 仿真结果
6.2.6 工程源码
传送门:https://download.csdn.net/download/pieces_thinking/10758660
不能下载的,私信我
6.3 CORDIC 算法的硬件实现(圆周系统)- 基于System Generator
内容太多了,另起一篇,大家移步:
基于System Generator的CORDIC算法实现
https://blog.csdn.net/Pieces_thinking/article/details/83745331