整数分划问题和钱的组合问题(动态规划)
问题1:整数分划问题
问题描述:对于一个正整数n的分划,就是把n表示成一系列正整数之和的表达式。需要注意的是,分划与顺序无关,例如6=5+1和6=1+5被认为是同一种分划。另外,这个整数n本身也算是一种分划。
例如,对于正整数n=6,它可以分划为:
6
5+1
4+2 4+1+1
3+3 3+2+1 3+1+1+1
2+2+2 2+2+1+1 2+1+1+1+1
1+1+1+1+1+1
从上面n=6的例子中可以看出,很难发现大问题P(n)和小问题P(n-d) (d=1,2,3,...)之间的关系。因此在解决本问题之前,先看另外一个问题:用递归法计算从n个人中选择k个人组成一个委员会的不同组合数。这个问题并不难,高三的排列组合问题,由分析可知:
由n个人里选k个人的组合数=由n-1个人里选k个人的组合数+由n-1个人选择k-1个人的组合数;这也是比较常见的排列组合公式: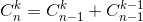
代码如下:
int comm(int n, int k){
if (k > n)
return 0;
else if (k == n || k == 0)
return 1;
else
return comm(n - 1, k) + comm(n - 1, k - 1);
}
下面来讨论Q(n,m)的递归关系:
(1)Q(n,n)=1+Q(n,n-1)
这个比较好理解,等式右边的1表示只包含一个被加数等于n本身的分划,其余的分划表示n的其他所有分划,即最大加数m<=n-1的分划。
(2)Q(n,1)=1
最大的被加数是1时,该整数只有一种分划,即n个1相加。
(3)Q(1,m)=1
表示整数1只有一个分划
(4)Q(n,m)=Q(n,m-1)+Q(n-m,m)
等式右边第一部分Q(n,m-1)表示被加数不包含m的分划的数目,第二部分表示被加数中包含(注意不是小于)m的分划的数目,因为如果确定了一个分划的被加数中包含m,则剩下的部分就是对n-m进行不超过m的划分。
代码如下:
int Divinteger(int n, int m){
if (n < 1 || m < 1)
return 0;
else if (n == 1 || m == 1)
return 1;
else if (n < m){
return Divinteger(n, n);
}
else if (n == m){
return 1 + Divinteger(n, n - 1);
}
else
return Divinteger(n, m - 1) + Divinteger(n - m, m);
}问题2:钱的组合问题
问题描述:有面值为1元、5元、10元、20元、50元、100元的纸币,每种纸币数量足够,需要求n元的不同纸币组合数,例如n=2时,组合数为1(两张1元),n=5时,组合数为2(一张5元或者5张一元)。
这问题可以用完全背包问题的思路求解,但是这里我们参照整数分划的思路,稍微不同的是,整数分划的加数可以取1,2,3...,n,但是钱的组合问题中加数只能取1,5,10,20,50,100,但是思路类似,这里我们可以声明一个数组V[6]={1,2,5,10,20,50}来表示纸币的面值,定义一个函数Q(n,m),表示n元的组合中“任何面值都不超过V[m]”分划的数目,n的所有分划数目P(n)就可以表示为Q(n,5)。
下面来讨论Q(n,m)的递归关系:
(1)Q(n,m)=Q(n,m-1)+Q(n-V[m],m) 思路类似于整数分划第一个公式
(2)Q(n,0)=1
(3)Q(1,m)=1
const int v[6] = { 1, 2, 5, 10, 20, 50 };
int f(int n, int w)
{
if (n<0) return 0;
if (n == 0) return 1;
if (w<0) return 0;
return f(n, w - 1) + f(n - v[w], w);
}