信用评分模型详解（上）之 评分卡模型

介绍完分箱算法后，就不得不介绍一下评分卡模型了。评分卡模型由于在业务层面具有良好的解释性，在数据挖掘方面（如风控）仍深受欢迎。

前提假设

目前，主流的评分卡模型仍以逻辑回归模型为主要模型。假设客户违约的概率为$p$，则正常的概率为$1-p$。由此可以得到违约几率：

$Odds=\frac{p}{1-p}$

此时，客户的违约概率$p$可以表示为：

$p=\frac{Odds}{1+Odds}$

评分卡设定的分值刻度可以通过将分值表示为几率对数的线性表达式来定义，即：

$Score=A\pm B\ast log(Odds)$

其中，A和B都是常数且（a>=0, b>=0）。当希望违约几率越低，得分越高时，取负号。通常情况下，这是分值的理想变动方向，即高分值代表低风险，低分值代表高风险。 所以，后面均讨论这种情况。

逻辑回归模型

对于逻辑回归模型，其目标函数为：

$p=h_{\theta }(x)=g(x)=\frac{1}{1+e^{(-{\theta }^{T}X)}}$

则计算几率的表达式如下：

$ln(Odds)=ln(\frac{p}{1-p})={\theta }_0+{\theta }_1\ast x_1+...+{\theta }_n\ast x_n$

其中，模型参数${\theta }_0,{\theta }_1,...,{\theta }_n$可以通过逻辑回归模型参数拟合模型得到。

评分卡构建

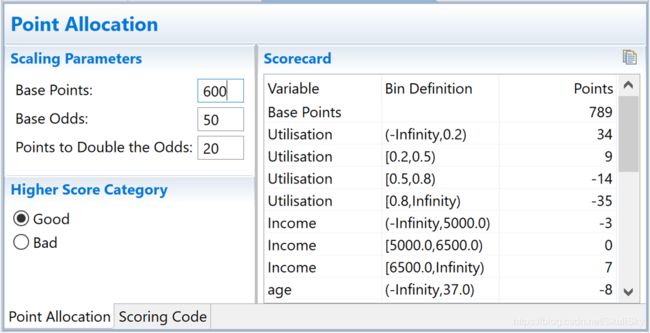
式中的常数A、B的值可以通过将两个已知或假设的分值计算得到。通常情况下，需要设定两个假设：
（1） 给定某个指定的几率${\beta }_0$，其对应的分值为基础分值$P_0$
（2）确定几率翻倍分值$PDO$。即当几率${\beta }_0$翻倍时，其对应的预期分值为$P_0+PDO$
根据上面的假设，可以将这两组点$({\beta }_0,P_0$),$(2{\beta }_0,P_0+PDO)$带入方程中，可以得到如下两个等式：

$P_0=A-Bln({\beta }_0)$
$P_0+PDO=A-Bln(2\ast {\beta }_0)$

解方程可得：

$A=P_0+B\ast ln({\beta }_0)$
$B=-PDO/ln2$

确定了评分卡刻度参数A和B以后，就可以计算比率和违约概率，以及对应的分值。
由上面的公式可知，评分卡的分值可表达为：

$Score=A-B\ast ({\theta }_0+{\theta }_1\ast x_1+...+{\theta }_n\ast x_n)$

式中，变量${\theta }_0...{\theta }_n$是出现在最终模型中的自变量，即为入模指标。

由于评分卡模型要求所有特征都经过WOE编码，所以，此时可以将自变量中的每一个值都写成如下形式：
$Score=(A-B\ast {\theta }_0)-(B\ast {\theta }_1\ast WO{E}_{11})-...(B\ast {\theta }_2\ast WO{E}_{21})-...$

此式即为最终的评分卡公式。如果$x_1...x_n$取不同的值并计算WOE值，式中表示的标准评分卡格式如下表所示：

变量	WOE值	分值
基础分值	$...$	$(A-B\ast {\theta }_0)$
$x_1$	1	$-(B\ast {\theta }_1\ast WO{E}_{11})$
$x_1$	2	$-(B\ast {\theta }_1\ast WO{E}_{12})$
$x_1$	$...$	$...$
$x_1$	$k_1$	$-(B\ast {\theta }_1\ast WO{E}_{1k_1})$
$x_2$	1	$-(B\ast {\theta }_2\ast WO{E}_{21})$
$x_2$	2	$-(B\ast {\theta }_2\ast WO{E}_{22})$
$x_2$	$...$	$...$
$x_2$	$k_2$	$-(B\ast {\theta }_2\ast WO{E}_{2k_2})$
$...$	$...$	$...$
$x_n$	1	$-(B\ast {\theta }_n\ast WO{E}_{n1})$
$x_n$	2	$-(B\ast {\theta }_n\ast WO{E}_{n2})$
$x_n$	$...$	$...$
$x_n$	$k_n$	$-(B\ast {\theta }_n\ast WO{E}_{n{k}_n})$

由此构建的评分卡系统如下所示：