一个简单线性回归网络在训练时误差越来越大

1 发现问题

PaddlePaddle官网上有一个简单的线性回归模型的例子，粘贴如下内容到新建的test.py中：

#加载库
import paddle.fluid as fluid
import numpy as np
#生成数据
np.random.seed(0)
outputs = np.random.randint(5, size=(10, 4))
res = []
for i in range(10):
        # 假设方程式为 y=4a+6b+7c+2d
        y = 4*outputs[i][0]+6*outputs[i][1]+7*outputs[i][2]+2*outputs[i][3]
        res.append([y])
# 定义数据
train_data=np.array(outputs).astype('float32')
y_true = np.array(res).astype('float32')

#定义网络
x = fluid.layers.data(name="x",shape=[4],dtype='float32')
y = fluid.layers.data(name="y",shape=[1],dtype='float32')
y_predict = fluid.layers.fc(input=x,size=1,act=None)
#定义损失函数
cost = fluid.layers.square_error_cost(input=y_predict,label=y)
avg_cost = fluid.layers.mean(cost)
#定义优化方法
sgd_optimizer = fluid.optimizer.SGD(learning_rate=0.05)
sgd_optimizer.minimize(avg_cost)
#参数初始化
cpu = fluid.CPUPlace()
exe = fluid.Executor(cpu)
exe.run(fluid.default_startup_program())
##开始训练，迭代500次
for i in range(500):
        outs = exe.run(
                feed={'x':train_data,'y':y_true},
                fetch_list=[y_predict.name,avg_cost.name])
        if i%50==0:
                print ('iter={:.0f},cost={}'.format(i,outs[1][0]))
#存储训练结果
params_dirname = "result"
fluid.io.save_inference_model(params_dirname, ['x'], [y_predict], exe)

# 开始预测
infer_exe = fluid.Executor(cpu)
inference_scope = fluid.Scope()
# 加载训练好的模型
with fluid.scope_guard(inference_scope):
        [inference_program, feed_target_names,
         fetch_targets] = fluid.io.load_inference_model(params_dirname, infer_exe)

# 生成测试数据
test = np.array([[[9],[5],[2],[10]]]).astype('float32')
# 进行预测
results = infer_exe.run(inference_program,
                                                feed={"x": test},
                                                fetch_list=fetch_targets)
# 给出题目为 【9,5,2,10】 输出y=4*9+6*5+7*2+10*2的值
print ("9a+5b+2c+10d={}".format(results[0][0]))

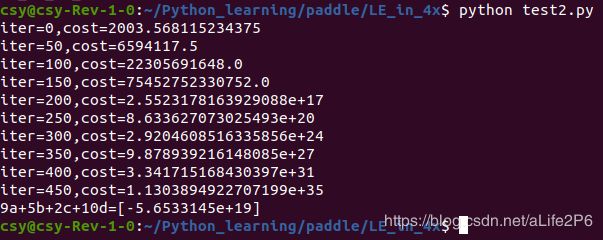
运行结果如下：

 学习效果蛮好的。

 因官网上要求用fluid.data 代替 fluid.layers.data，故将程序稍作了一点改动：

1. 将 fluid.layers.data 改为 fluid.data

1.1相应的x的shape改为[-1,4]，y的shape改为[-1,1]

x = fluid.data(name="x",shape=[-1,4],dtype='float32')
y = fluid.data(name="y",shape=[-1,1],dtype='float32')

 1.2测试数据的shape改为[1,4]

test = np.array([[9,5,2,10]]).astype('float32')

2. 想增加模型的准确度，将训练数据由10组增加到20组

outputs = np.random.randint(5, size=(20, 4))
for i in range(20):

修改后的代码如下，另存为 test2.py

#加载库
import paddle.fluid as fluid
import numpy as np
#生成数据
np.random.seed(0)
outputs = np.random.randint(5, size=(20, 4))
res = []
for i in range(20):
        # 假设方程式为 y=4a+6b+7c+2d
        y = 4*outputs[i][0]+6*outputs[i][1]+7*outputs[i][2]+2*outputs[i][3]
        res.append([y])
# 定义数据
train_data=np.array(outputs).astype('float32')
y_true = np.array(res).astype('float32')

#定义网络
x = fluid.data(name="x",shape=[-1,4],dtype='float32')
y = fluid.data(name="y",shape=[-1,1],dtype='float32')
y_predict = fluid.layers.fc(input=x,size=1,act=None)
#定义损失函数
cost = fluid.layers.square_error_cost(input=y_predict,label=y)
avg_cost = fluid.layers.mean(cost)
#定义优化方法
sgd_optimizer = fluid.optimizer.SGD(learning_rate=0.05)
sgd_optimizer.minimize(avg_cost)
#参数初始化
cpu = fluid.CPUPlace()
exe = fluid.Executor(cpu)
exe.run(fluid.default_startup_program())
##开始训练，迭代500次
for i in range(500):
        outs = exe.run(
                feed={'x':train_data,'y':y_true},
                fetch_list=[y_predict.name,avg_cost.name])
        if i%50==0:
                print ('iter={:.0f},cost={}'.format(i,outs[1][0]))
#存储训练结果
params_dirname = "result"
fluid.io.save_inference_model(params_dirname, ['x'], [y_predict], exe)

# 开始预测
infer_exe = fluid.Executor(cpu)
inference_scope = fluid.Scope()
# 加载训练好的模型
with fluid.scope_guard(inference_scope):
        [inference_program, feed_target_names,
         fetch_targets] = fluid.io.load_inference_model(params_dirname, infer_exe)

# 生成测试数据
test = np.array([[9,5,2,10]]).astype('float32')
# 进行预测
results = infer_exe.run(inference_program,
                                                feed={"x": test},
                                                fetch_list=fetch_targets)
# 给出题目为 【9,5,2,10】 输出y=4*9+6*5+7*2+10*2的值
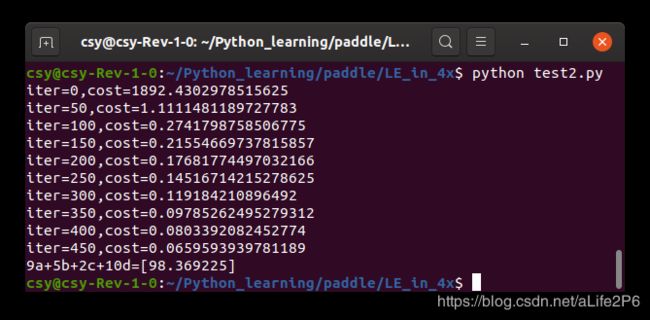
print ("9a+5b+2c+10d={}".format(results[0][0]))

运行结果如下：

奇怪的事情出现了：训练数据增加，不但没有使机器学习的成绩变好，反而越学越差了。

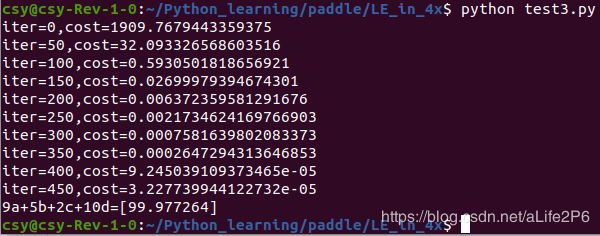
若将数据增加到30组

outputs = np.random.randint(5, size=(30, 4))
for i in range(30):

修改后的代码如下，另存为test3.py

#加载库
import paddle.fluid as fluid
import numpy as np
#生成数据
np.random.seed(0)
outputs = np.random.randint(5, size=(30, 4))
res = []
for i in range(30):
        # 假设方程式为 y=4a+6b+7c+2d
        y = 4*outputs[i][0]+6*outputs[i][1]+7*outputs[i][2]+2*outputs[i][3]
        res.append([y])
# 定义数据
train_data=np.array(outputs).astype('float32')
y_true = np.array(res).astype('float32')

#定义网络
x = fluid.data(name="x",shape=[-1,4],dtype='float32')
y = fluid.data(name="y",shape=[-1,1],dtype='float32')
y_predict = fluid.layers.fc(input=x,size=1,act=None)
#定义损失函数
cost = fluid.layers.square_error_cost(input=y_predict,label=y)
avg_cost = fluid.layers.mean(cost)
#定义优化方法
sgd_optimizer = fluid.optimizer.SGD(learning_rate=0.05)
sgd_optimizer.minimize(avg_cost)
#参数初始化
cpu = fluid.CPUPlace()
exe = fluid.Executor(cpu)
exe.run(fluid.default_startup_program())
##开始训练，迭代500次
for i in range(500):
        outs = exe.run(
                feed={'x':train_data,'y':y_true},
                fetch_list=[y_predict.name,avg_cost.name])
        if i%50==0:
                print ('iter={:.0f},cost={}'.format(i,outs[1][0]))
#存储训练结果
params_dirname = "result"
fluid.io.save_inference_model(params_dirname, ['x'], [y_predict], exe)

# 开始预测
infer_exe = fluid.Executor(cpu)
inference_scope = fluid.Scope()
# 加载训练好的模型
with fluid.scope_guard(inference_scope):
        [inference_program, feed_target_names,
         fetch_targets] = fluid.io.load_inference_model(params_dirname, infer_exe)

# 生成测试数据
test = np.array([[9,5,2,10]]).astype('float32')
# 进行预测
results = infer_exe.run(inference_program,
                                                feed={"x": test},
                                                fetch_list=fetch_targets)
# 给出题目为 【9,5,2,10】 输出y=4*9+6*5+7*2+10*2的值
print ("9a+5b+2c+10d={}".format(results[0][0]))

运行结果如下：

哇！学习成绩又提高了。比10组数据训练还要好。

2 查找问题

为了查找问题，对程序进行了一些修改和简化：

1.改为用键盘输入数字确定组数，生成训练数据
2.改为用键盘输入数字确定生成的训练数据范围
3.改为用键盘输入数字确定随机种子
5.随机产生浮点数的训练数据
6.打印出训练数据
7.不保存模型
8.删除测试部分

修改后的代码如下，另存为test7.py

#加载库
import paddle.fluid as fluid
import numpy as np

#生成数据
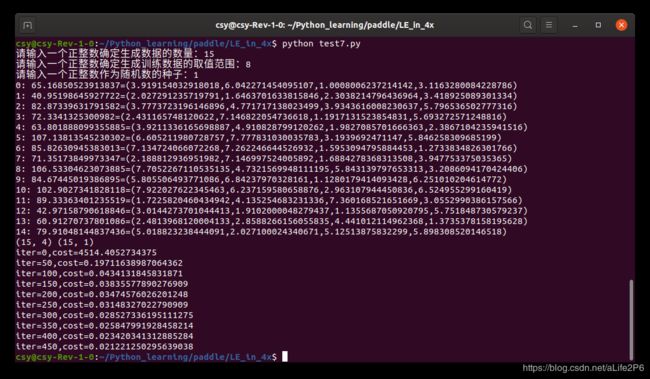
group = input('请输入一个正整数确定生成数据的数量：')
group = int(group)
data_range = input('请输入一个正整数确定生成训练数据的取值范围：')
float_range = float(data_range)
random_seed = input('请输入一个正整数作为随机数的种子：')

np.random.seed(int(random_seed))
outputs =np.random.uniform(1,float_range,size=(group,4)) #float64

res = []  #生成一个空list
for i in range(group):
    #假设方程式为 y=4a+6b+7c+2d，生成答案
    y = 4*outputs[i][0]+6*outputs[i][1]+7*outputs[i][2]+2*outputs[i][3]
    print("{}: {}=({},{},{},{})".format(i,y,outputs[i][0],outputs[i][1],outputs[i][2],outputs[i][3]))
    res.append([y])  # 当变量为array[][]时，对应的y值保存在res

# 定义数据
train_data = np.array(outputs).astype('float32')   # 训练数据使用10组随机生成的数据，将整型随机数改为浮点型
y_true = np.array(res).astype('float32')           # 对应的标准答案
print(train_data.shape,y_true.shape)

# 定义网络
x = fluid.data(name="x",shape=[None,4],dtype='float32')
y = fluid.data(name="y",shape=[None,1],dtype='float32')
y_predict = fluid.layers.fc(input=x,size=1,act=None)

# 定义损失函数
cost = fluid.layers.square_error_cost(input=y_predict,label=y)
avg_cost = fluid.layers.mean(cost)

# 定义优化
sgd_optimizer = fluid.optimizer.SGD(learning_rate=0.05)
sgd_optimizer.minimize(avg_cost)

#参数初始化
cpu = fluid.CPUPlace()
exe = fluid.Executor(cpu)
exe.run(fluid.default_startup_program())

## 开始训练，迭代500次
for i in range(500):
    outs = exe.run(
        feed={'x':train_data,'y':y_true},
        fetch_list=[y_predict.name,avg_cost.name])
    if i%50==0:
        print('iter={:.0f},cost={}'.format(i,outs[1][0]))

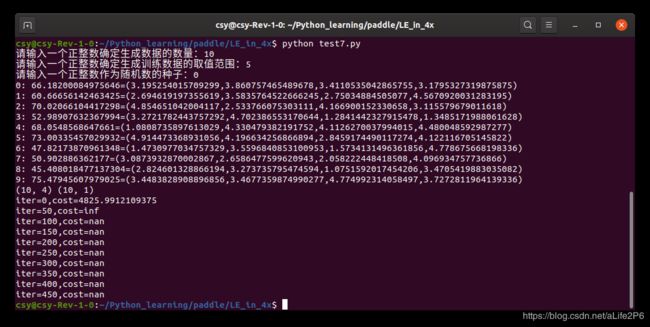
第一次运行：

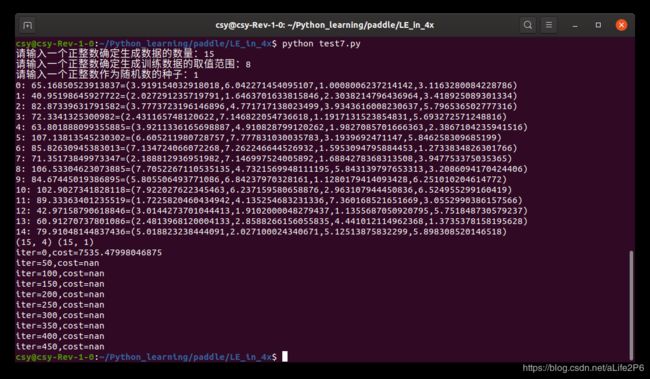
第二次运行：

将学习率改为0.01

sgd_optimizer = fluid.optimizer.SGD(learning_rate=0.01)

运行结果：

 再将test2.py的学习率修改为0.01，运行结果：

 学习率降低后，每次训练都有进步，只是进步不大。但不会退步。

3 我的结论

训练数据的shape和type，必须和fluid.data的shape和type一致。训练数据的shape和type，也必须和fluid.data的shape和type一致。

学习率高，相当于学生跳级。顺利的话，比别的学生学的快，早毕业。但是也可能不如按部就班的学生有进步，也就是有拔苗助长的风险。学习率低，可以做到天天向上。要在稳健和速度上进行调整。

训练的数据范围最好要涵盖测试数据的范围。考试题如果是老师上课讲过的，考试成绩就会好一些。

训练数据的数量越大，损失函数的值越漂亮。如果相反，则应考虑学习率是否需要调低一些。

对于学习率低的网络，可以采取笨鸟先飞的办法，多迭代几次来弥补进步慢的不足。当然也要警惕迭代过多可能引起过拟合。