数据库索引背后的数据结构之B-树和B+树

前言：索引结构有B树索引、Hash索引、Fulltext索引等，关于树结构的索引又分为B-Tree、B+Tree、B*Tree、R树、R+树等。本文重点探讨B树的前两种结构。

数据库查询为什么要使用索引

  从理论上讲，假设数据库中的某一个表有 108 条记录，数据库管理系统一个页面大小4KB，最多能存放100条记录。那么 108 条记录将分成 106 页来存储，总的存储开销为4KB* 106 =3906MB=3.8GB。假设计算机的内存为2GB，那么至少会有1.8GB*1024*1024=47万个页面存放在磁盘上，当进程处理时发现所需的页面在内存中不存在，则会发生缺页中断。如果页面在磁盘上是随机存储的，则需要47万次I/O操作。假设每次I/O操作的时间为10ms，那么至少需要78分钟，这显然是一次十分低效的查询操作。为了提高查询效率，需要为数据建立索引。在MySQL数据库管理系统中普遍使用的是B+Tree索引。对数据建立了B+Tree索引之后，查找所需的页面只需 log100(108)=4 次I/O操作（这里假设这四个用来索引的页面都在磁盘上），所花的时间为40ms，查找时间将缩短成千上万倍。以上计算属于估计值，读者领会其中的意思即可。由此可见，在数据量庞大的情况下，使用索引查询数据库非常有效。

索引数据结构剖析

  索引是一种加快检索速度的数据结构。在很多数据库管理系统中都大量使用了B+Tree，B+Tree是由B-Tree改进而来的。只有彻底地理解了这两种数据结构，才能做好基于索引的数据库查询优化。下面通过计算机的存储机制来详细介绍这两种数据结构。

B-Tree

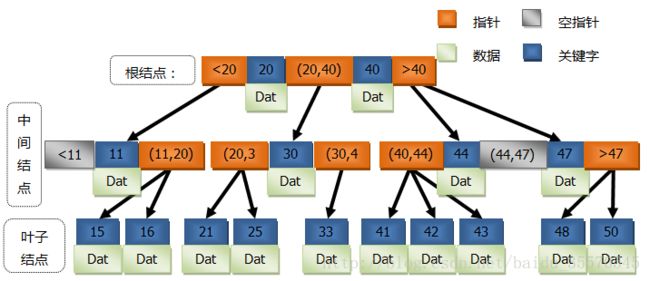
  B-Tree是一棵多路搜索树，对于每个非叶子结点都存在关键字和指针，关键字的作用是对目标数据进行比对，以缩小目标数据的搜索范围，指针用来指向下一层的某个结点。对于 m（m>2） 阶的B-Tree，有限制条件如下：
- 树的任意结点最多有 m 个子树，是特殊的 m 叉树；
- 根结点的子树个数必须满足 [2,m] ；
- 所有叶子节点处在同一高度，所以称之为特殊 m 叉树；
- 处在中间层的结点(除根结点和叶子结点)的子树个数必须满足 [m2,m] ，这意味着中间层的任意结点不能没有子树；
- 关键字数=指针数+1，因为在一维空间上 k 个分隔点可以分成 k+1 的区间；
- 非叶子结点的关键字有 m−1 个，由上一条规则可知非叶子结点的指针数为 m 个，并且所有非叶子结点的关键字按照统一的顺序排列，这里指升序或降序。
- 指针 P[1] 所指的结点的关键字都小于 K[1] ，指针 P[m] 所指的结点的关键字都大于 K[m−1] ，中间的指针 P[i] 所指结点的关键字满足 (K[i],K[i+1]) ，注意这里是开区间，与B+Tree不同。

图1为一棵三阶的B-Tree示意图。

图1

注意：在每个关键字上都会附有所要查找的数据

  这意味着当你正在搜索某个数据的时候，无需每次都从根结点访问到叶子结点，比如当需要搜索关键字11所代表的数据时，只要检索到中间结点即可。当然，这就是它相对于B+Tree的优点，在某种程度上提高了搜索的效率。
  由于B-Tree的每个结点上的关键字排列有序，因此搜索数据可以借鉴于折半查找（二分查找）。

问：为什么要这样去设计B树呢？

  由于计算机的内存是有限的，所以我们要充分利用留在内存中的索引页面。为什么这么说？当存储的数据量达到巨大的时候，很难保证索引页面都留在内存中，当然这也是极不可能的，总会有一部分索引页面存储在磁盘上，当所要查找的数据的索引不在内存时才去调度磁盘上的索引页面。CPU处理作业时只和内存打交道，内存的页面调度时间相对于外存要小好几个数量级，可是对于外存与内存之间的页面调度（I/O操作）是相当耗时的，所以我们要尽量使I/O操作次数最少，同时又能达到搜索数据的目的，这就是我所说的“充分利用”。
  B树相比较二叉平衡树或者红黑树而言最大的优点是利用尽可能大的度数来降低树高。B-树上大部分基本操作所需访问盘的次数均取决于树高。具体计算如下：
若n≥1，m≥3，则对任意一棵具有n个关键字的m阶B-树，其树高h至多为

logt(n+12)+1

这里t是每个(除根结点外)内部结点的最小度数，即

⌈m2⌉

所以，树的高度为h。此外，数据库系统巧妙利用了页面的大小，将一个结点的大小设为等于一个页，这样每个结点只需要一次I/O就可以完全载入，最大程度地减少了I/O次数。

B+Tree

  B+Tree是对B-Tree的改进，并且广泛应用于数据库管理系统中。其与B-Tree在数据结构上有两点区别：
- 每个非叶子结点的关键字数等于其孩子数，也就是说关键字数等于指针数；
- 所有数据都在叶子结点上.

  B+Tree的指针所指的区间是左闭右开或左开右闭，图2为一棵二阶的B+Tree示意图，图中的指针所指向的数都比其左边的关键字大。

图2

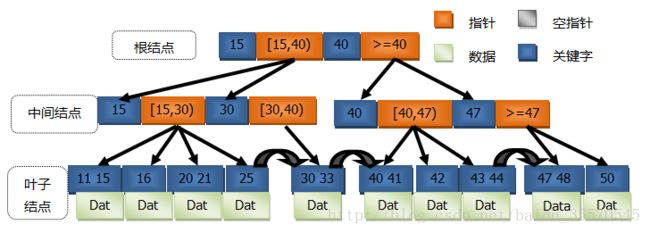
  在DBMS中通常会将叶子结点通过指针相连接，为什么要这么做呢？这是为了方便相邻叶子结点之间的访问，不必每次都从根结点开始访问。例如，有这样一条sql语句：

select field_name from table where field_name > 24 and field_name < 31.

  知道根据图2的数据，不管全表扫描也好，走索引也好，最终都会返回25和30，而B+Tree是效率最高的，它的搜索路径是先从根结点索引到25，紧接着根据指向下一个叶子结点的指针可以迅速找到30。针对这种连续数据块的搜索，这种数据结构是正是其优势所在。

联合索引与最左前缀原则

联合索引

  上文所讲的索引树是对于同一个字段的数据，这里讲解多个字段的联合索引。为了清晰的描述问题，给出表1数据：

表1

职称	月薪	姓名
讲师	3100	孙权
副教授	8000	曹操
讲师	9000	于吉
教授	5000	周瑜
副教授	4500	关羽
副教授	5600	张飞
教授	7600	黄盖
讲师	4000	诸葛亮
教授	7500	刘备
副教授	6000	张昭
教授	6500	大乔
讲师	5500	小乔
教授	9000	马超
讲师	5600	黄忠
副教授	6500	赵云

  接下来我要查找月薪为6500的副教授的名字，sql语句为：

select 姓名 from [table] where 职称 = '副教授' and 月薪 = 6500. 

最慢的方法无疑是全表扫描，其执行过程是这样的：顺序查找职称为副教授的数据行，找到后与月薪进行比对；第二种方法是对职称建立索引，这样就能快速定位到副教授，但对于月薪这一列还需一一比对；第三种方法与第二种方法类似，是对月薪建立索引，又因为月薪的选择性高，

索引的选择性：索引列中不同值的数目与表中记录数的比。

所以相比较职称而言，对月薪建立索引更加有效；第四种方法是对职称和月薪建立联合索引，这种方法效率最高。联合索引是按先后顺序对两列进行排序，就是先对职称排序，然后再对月薪排序，注意必须按先来后到的关系，月薪是在某一个职称下进行排序后的结果。联合索引其实就是“树中有树”的思想。表2为联合索引后的结果。

表2

职称	月薪	姓名
讲师	3100	孙权
讲师	4000	诸葛亮
讲师	5500	小乔
讲师	5600	黄忠
讲师	9000	于吉
副教授	4500	关羽
副教授	5600	张飞
副教授	6000	张昭
副教授	6500	赵云
副教授	8000	曹操
教授	5000	周瑜
教授	6500	大乔
教授	7500	刘备
教授	7600	黄盖
教授	9000	马超

最左前缀原则

  如果对column1，column2，column3建立了联合索引，那么在使用该索引时只有三种组合，它们分别是：column1 、column1 and column2、column1 and column2 and column3，概括起来就是想要使用右边的索引，必须用上左边的所有索引。如果只使用column2作为where的查询条件，将不会用到所建好的索引。这是为什么呢？请看表2。这就好比直接用月薪作为查询条件，有没有发现月薪是呈全局乱序的状态，尽管它是局部有序的。如果业务上要求只能用月薪来查询，可行的解决办法是在建立联合索引时把月薪放在最左边，或者直接建立单列索引。

总结

  上文主要介绍了两种树形索引结构，由于本文的侧重点是查询优化，所以并未在树的建立与删除上费口舌。要知道，数据结构是计算机技术能够快速发展到今天的基础，只有对数据结构研究透彻了，才能在索引优化上有所突破。我们发现在执行数据库的时候，不同的sql语句的写法可能会造成千差万别的效率，所以做数据库的优化的时候，我们要保持严谨谦逊的心态，要深刻理解研究其内部的数据结构原理，知道是什么、为什么、该怎么做、不这么做会怎么样。

参考文献:
[1] MySQL索引背后的数据结构及算法原理，2011.
[2] 索引与优化，2009.
[3] 王正万: ‘MySQL索引分析及优化’, 黔东南民族师范高等专科学校学报, 2006, 24, (3), pp. 54-55
[4] 何爱华, 郭有强: ‘查询优化之索引的设计’, 蚌埠学院学报, 2012, 1, (2), pp. 24-26
[5] 伍应树, 赵志刚, 李宪明: ‘关系数据库基于索引查询的优化设计研究’, 电脑编程技巧与维护, 2016, 0, (17), pp. 56-58
[6] 魏威, 马国峰: ‘基于索引的关系数据库查询优化’, 洛阳大学学报, 2007, 22, (2), pp. 83-86

---

非常感谢阅读水浴月研究生生涯的第一篇博文，本人才疏学浅，希望和大家一同进步！