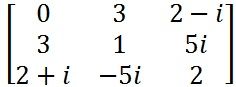数学的故事之“共轭”

中国古人研究数学的历史能追溯到好几千前，例如勾股定理的文字记载最早出现在《周髀算经》（约公元前1世纪）中，而书中记载的关于这条定理的源起则更是古老：公元前十一世纪，周朝数学家商高同周公的一段对话中提到“勾三、股四、弦五”这样一种奇妙的关系。后来，到了明清时代，中国数学家开始从大量从传教士那里了解到了更多的西方数学成果。从这个时候开始，就逐渐出现了很多关于西方数学名词的译法，而且绝大部分都一直沿用至今。但这其实也带来了一个麻烦，那就是现代人（除了专攻古典文学专业的人以外）的文言文水平早已远不及古人。又或者很多古代司空见惯的词到今时今日也已经较少被使用。于是，当面对可能来自于古代的数学用语时，尽管今天它在数学中仍然被广泛的使用，但是由于缺乏直观上的认识，往往会带给很多初学者以困惑。这里比较典型的一个例子就是“共轭”。

共轭在数学、物理、化学、地理等学科中都有出现，甚至在数学上也有许许多多的“共轭”，例如：共轭复数、共轭矩阵和共轭分布等等。有些不了解的人往往会觉得这些概念之间是不是有什么内在的联系，或者一个概念是另外一个概念的推广，就像二氧化碳、二氧化硅和二氧化硫的关系一样。然而事实并非如此！它们唯一的联系，也仅仅是抽象地体现出了共轭这种关系，但显然矩阵并不是可能是复数的推广。从分子结构来说，二氧化碳和二氧化硫的结构上都有两个氧原子，但是从（一对儿）共轭复数和（一对儿）共轭分布上，你是绝对找不到所谓“结构”上的共有组分的。

“轭”字的本意是驾车时套在牲口脖子上的曲木，引申为束缚或控制的意思。显然，因为现代中国早已不是一个农耕社会，所以让一个“五谷不分”的学生去理解或解释什么是轭，恐怕有点不太容易。既然轭是套在牲口脖子上的曲木，那么显然共轭就是套在两头牲口脖子上的曲木，或者说是两头牲口共用同一根曲木之意。

再回过头来看看英语中共轭那个词的意思“conjugate”：“con”是一个非常常用的英语词根，表示“共同”之意思。例如，

confluence汇流（con+flu流＋ence→共同流→汇流）

concentric同中心的(con+centric中心的→共同中心的)

contemporary同时代的(con+tempor时间+ary→同时间的)

而jugate来自于拉丁语，意思是“together in pairs”，作为形容词可以表示“forming a pair”，也就是构成一对儿的。所以conjugate就是指（两个个体）共同构成了一对儿（这样的关系）。

下面我们就来看看数学里面哪些东西可以构成一个共轭对儿。首先，最简单的是共轭复数。两个实部相等，虚部互为相反数的复数互为共轭复数(conjugate complex number)（当虚部不等于0时也叫共轭虚数）。例如1+2i 和1-2i 就是一对儿共轭复数。

另外一个你可能需要知道的概念是“共轭矩阵”。如果矩阵 A 是一个实矩阵（即矩阵中的元素都是实数），且矩阵中的元素有 A(i, j) = A(j, i)，那么我们称这个矩阵是一个对称矩阵。如果把这个矩阵扩展到复数域（即允许矩阵中的元素时复数），并要求按对角线对称的两个位置上的元素彼此之间是共轭复数关系，即，那么我们就称这个矩阵是一个共轭矩阵，又称为埃尔米特（Hermite）矩阵。例如：

夏尔·埃尔米特（Charles Hermite，1822~1901）十九世纪法国出现的最伟大的代数几何学家。法兰西科学院院士。巴黎综合理工学院毕业，后来曾在巴黎高等师范学校任教。他在在函数论、高等代数、微分方程等方面都有重要发现。埃尔米特的大学入学考试重考了五次，每次失败的原因都是数学考不好。他的大学读到几乎毕不了业，每次考不好都是数学那一科。他大学毕业后考不上任何研究所，因为考不好的科目还是数学。数学是他一生的至爱，但是数学考试是他一生的恶梦。不过这无法改变他的伟大：课本上的“共轭矩阵”是他最先提出来的；自然常数e的“超越数性质”也是他第一个证明出来的。他的一生证明“一个不会考试的人，仍然能有胜出的人生”，并且更奇妙的是不会考试成为他一生的祝福。

当然，初看共轭矩阵这个概念，你会觉得有点不足为奇。但如果同泛函中的某些结论结合起来看，这就变成了一个相当深奥的知识了！首先我们知道，泛函中的一个算子都可以由一个对应的矩阵形式来表示，反之亦然。而在线性代数中，我们应该都学过矩阵A的共轭转置矩阵A*。共轭转置矩阵其实又对应了泛函中的伴随（adjoint）算子这个概念。算子T的伴随算子T*（相对于orthonormal基底β）的矩阵表示 就等于 算子T（相对于orthonormal基底β）的矩阵表示的共轭转置。根据这个定理我们很容易得到如下推论：(L_A)*=L_A* 。更重要的是这个定理还为寻找T的T*提供了一种途径。

此外，如果有AA*=A*A，则我们就可以称矩阵A是normal的。更重要的是我们还可以证明：A=M_n×n(C)，A是normal的 ⇔ A 可以对角化。如果T（或A）是self-adjoint的，那么它也一定是normal的，而self-adjoint的意思对于算子而言就是自伴随，对于矩阵而言就是自共轭，即A = A*。也就是说，居然转置后再取共轭就会变成它本身的样子。A和A*互为共轭转置，所以A就是我们前面所说的Hermite矩阵。

根据线性代数的理论可知：当Field是C时，Normal就是可对角线化的充要条件。现在我们想知道如果Field是R时，是否还能找到一个用于判定矩阵（或算子）是否可对角化的简单标准。事实上，当Field是R时，self-adjoint 就是可对角线化的充要条件。

你可能会认为共轭矩阵中其实也有共轭复数的操作，似乎从这个角度能把它们联系到一起。但是如果换成泛函中的self-adjoint 算子，那么这点联系就已经非常不明显了。这其实就告诉我们，共轭与否未必都是以共轭复数这个角度作为出发点的。更重要的是，它们共同形成了“一对儿”这样的关系，这才是共轭的本质。如果你认为这还不能完全令你信服，那么另外一个重要也是最后一个，我认为你应该知道的数学中的共轭关系，就是共轭分布。在概率论中，如果后验概率分布拥有与先验分布相同的函数形式，那么这个性质被叫做共轭性（conjugacy）。如果两个分布之间存在共轭性，那么它们就是一对儿共轭分布。例如，二项分布的参数之共轭先验就是我们前面介绍的 Beta 分布。多项式分布的参数之共轭先验则是 Dirichlet 分布，⽽⾼斯分布的均值之共轭先验是另⼀个⾼斯分布。关于共轭分布更多的内容，你还可以参考《先验概率、后验概率以及共轭先验 》一文。

更多有用的数学知识，你还可以参考《图像处理中的数学修炼》一书。