线段树、主席树习题
线段树习题
- Count the Colors ZOJ - 1610 (区间染色)
- Mayor's posters POJ - 2528 (离散化 + 区间染色)
- B. Light bulbs (离散化)
- F. Greedy Sequence (滑动窗口 || 线段树 || 主席树)
- array HDU - 6703
- H Cutting Bamboos 2019牛客暑期多校训练营(第九场)
- E. Find the median 2019牛客第七场 (线段树)
Count the Colors ZOJ - 1610 (区间染色)
题意:给定 l、r、c 表示将两个端点 [ l , r ] [l,r] [l,r] 的颜色覆盖为 c。输出覆盖以后,最终能够看到的颜色和这种颜色出现的段数
链接:https://vjudge.net/problem/ZOJ-1610
#include <bits/stdc++.h>
#define ll long long
#define ls (rt<<1)
#define rs (rt<<1|1)
using namespace std;
const int maxn=8000+10;
int n;
int st[maxn<<2];
void pushDown(int rt)
{
if(st[rt]!=-1)
{
st[ls]=st[rt];
st[rs]=st[rt];
st[rt]=-1;
}
}
void build(int rt,int L,int R)
{
st[rt]=-1;
if(L==R) return;
int mid=(L+R)>>1;
build(ls,L,mid);
build(rs,mid+1,R);
}
void update(int rt,int l,int r,int L,int R,int c)
{
if(l<=L&&R<=r)
{
st[rt]=c;
return;
}
pushDown(rt);
int mid=(L+R)>>1;
if(l<=mid) update(ls,l,r,L,mid,c);
if(r>mid) update(rs,l,r,mid+1,R,c);
}
int last;
map<int,int> mp;
void query(int rt,int L,int R)
{
if(L==R)
{
if(st[rt]==-1) last=st[rt];
else if(st[rt]!=last)
{
mp[st[rt]]++;
last=st[rt];
}
return;
}
pushDown(rt);
int mid=(L+R)>>1;
query(ls,L,mid);
query(rs,mid+1,R);
}
int main()
{
while(~scanf("%d",&n))
{
mp.clear();
build(1,1,8000);
for(int i=1;i<=n;++i)
{
int l,r,dx;
scanf("%d%d%d",&l,&r,&dx);
if(l+1>r) continue;
update(1,l+1,r,1,8000,dx);
}
last=-1;
query(1,1,8000);
for(auto x : mp)
{
int col=x.first,seg=x.second;
printf("%d %d\n",col,seg);
}
puts("");
}
return 0;
}
Mayor’s posters POJ - 2528 (离散化 + 区间染色)
链接:https://cn.vjudge.net/problem/POJ-2528
题意:给定一些区间,对这些区间染色,问最终能看到多少不同的颜色。
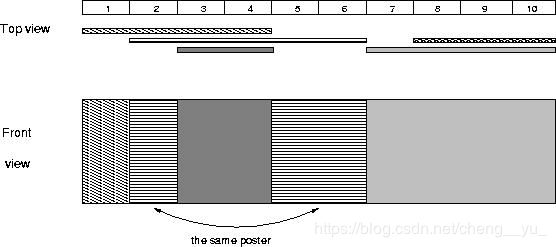
输入:
1
5
1 4
2 6
8 10
3 4
7 10
输出:
4
思路:离散化
#include <cstdio>
#include <vector>
#include <map>
#include <cstring>
#include <algorithm>
#define ls (rt<<1)
#define rs (rt<<1|1)
#define fi first
#define se second
#define ll long long
using namespace std;
const int maxn=2e4+10;
int t,n;
vector<int> allx;
pair<int,int> p[maxn];
map<int,bool> visit;
int st[maxn<<2];
void pushDown(int rt)
{
if(st[rt]!=-1)
{
st[ls]=st[rt];
st[rs]=st[rt];
st[rt]=-1;
}
}
void update(int rt,int l,int r,int L,int R,int val)
{
if(l<=L&&R<=r)
{
st[rt]=val;
return;
}
pushDown(rt);
int mid=(L+R)>>1;
if(l<=mid) update(ls,l,r,L,mid,val);
if(r>mid) update(rs,l,r,mid+1,R,val);
}
int last,ans;
void query(int rt,int L,int R)
{
if(st[rt]!=-1&&last!=st[rt])
{
if(!visit.count(st[rt]))
ans++,visit[st[rt]]=1;
last=st[rt];
return;
}
if(L==R)
{
last=st[rt];
return;
}
pushDown(rt);
int mid=(L+R)>>1;
query(ls,L,mid);
query(rs,mid+1,R);
}
int main()
{
scanf("%d",&t);
while(t--)
{
memset(st,-1,sizeof(st));
allx.clear();
visit.clear();
scanf("%d",&n);
for(int i=1;i<=n;++i)
{
int l,r;
scanf("%d%d",&l,&r);
l--;
p[i].fi=l,p[i].se=r;
allx.push_back(l);
allx.push_back(r);
}
sort(allx.begin(),allx.end());
allx.resize(unique(allx.begin(),allx.end())-allx.begin());
int tot=allx.size();
for(int i=1;i<=n;++i)
{
int l=lower_bound(allx.begin(),allx.end(),p[i].fi)-allx.begin()+1;
int r=lower_bound(allx.begin(),allx.end(),p[i].se)-allx.begin();
update(1,l,r,1,tot-1,i);
}
last=-1;
ans=0;
query(1,1,tot-1);
printf("%d\n",ans);
}
return 0;
}
B. Light bulbs (离散化)
链接:https://www.jisuanke.com/contest/3003/challenges
题意:给定区间翻转的操作,问最后亮灯的数量
思路:用异或维护翻转操作即可。
#include <bits/stdc++.h>
#define ls (rt<<1)
#define rs (rt<<1|1)
#define fi first
#define se second
#define ll long long
using namespace std;
const int maxn=1000+10;
int t,n,m;
vector<int> allx;
pair<int,int> p[maxn<<1];
int st[maxn<<3],lazy[maxn<<3];
void pushDown(int rt,int L,int R)
{
if(lazy[rt])
{
int mid=(L+R)>>1;
st[ls]=allx[mid]-allx[L-1]-st[ls];
st[rs]=allx[R]-allx[mid]-st[rs];
lazy[ls]^=lazy[rt];
lazy[rs]^=lazy[rt];
lazy[rt]=0;
}
}
void build(int rt,int L,int R)
{
st[rt]=lazy[rt]=0;
if(L==R) return;
int mid=(L+R)>>1;
build(ls,L,mid);
build(rs,mid+1,R);
}
void update(int rt,int l,int r,int L,int R)
{
if(l<=L&&R<=r)
{
st[rt]=allx[R]-allx[L-1]-st[rt];
lazy[rt]^=1;
return;
}
pushDown(rt,L,R);
int mid=(L+R)>>1;
if(l<=mid) update(ls,l,r,L,mid);
if(r>mid) update(rs,l,r,mid+1,R);
st[rt]=st[ls]+st[rs];
}
int query(int rt,int L,int R)
{
if(L==R) return st[rt];
pushDown(rt,L,R);
int ans=0;
int mid=(L+R)>>1;
return query(ls,L,mid)+query(rs,mid+1,R);
}
int main()
{
scanf("%d",&t);
int Case=0;
while(t--)
{
scanf("%d%d",&n,&m);
allx.clear();
for(int i=1;i<=m;++i)
{
int l,r;
scanf("%d%d",&l,&r);
r++;
p[i].fi=l,p[i].se=r;
allx.push_back(l);
allx.push_back(r);
}
sort(allx.begin(),allx.end());
allx.resize(unique(allx.begin(),allx.end())-allx.begin());
int tot=allx.size()-1;
build(1,1,tot);
for(int i=1;i<=m;++i)
{
int l=lower_bound(allx.begin(),allx.end(),p[i].fi)-allx.begin()+1;
int r=lower_bound(allx.begin(),allx.end(),p[i].se)-allx.begin();
update(1,l,r,1,tot);
}
printf("Case #%d: %d\n",++Case,query(1,1,tot));
}
return 0;
}
F. Greedy Sequence (滑动窗口 || 线段树 || 主席树)
链接:https://nanti.jisuanke.com/t/41303
题意:给定一个 n 的排列,对于每个数 i,它的位置为 p o s [ i ] pos[i] pos[i] ,查找 [ p o s [ i ] − k , p o s [ i ] + k ] [pos[i]-k,pos[i]+k] [pos[i]−k,pos[i]+k] 中小于第一个小于 i 的数 x ,答案就是 a n s [ i ] = a n s [ x ] + 1 ans[i]=ans[x]+1 ans[i]=ans[x]+1。
简单的说,就是在给定区间内,查找第一个小于 i 的数。
思路:
- 滑动窗口:这里比较特殊, a i a_i ai 是序列上的一个数,可以用set 维护一个长度为 k 的区间,然后搜出左边 k 个中的小于 a i a_i ai 最大值,右边 k 个中的小于 a i a_i ai 最大值,最后两边取最大值即可
- 线段树:先将小于自己的数先更新到线段树上,然后就查询这个区间上的最大值,就找到了。边更新边寻找答案。对自己答案有贡献的做更新,有影响的先不更新。
- 主席树:在主席树上区间 [ l , r ] [l,r] [l,r] 表现为时间序,小于 i i i 表现为 i 的位置 p 左边第一个有数的位置,即从位置 p -1 找到 1 。
滑动窗口
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e5+10;
int t,n,k;
int a[maxn],ans[maxn];
int l[maxn],r[maxn];
int pos[maxn];
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;++i) scanf("%d",&a[i]),pos[a[i]]=i;
for(int i=1;i<=n;++i) ans[i]=l[i]=r[i]=0;
set<int> s;
for(int i=1;i<=n;++i)
{
if(i-k-1>=1) s.erase(a[i-k-1]);
s.insert(a[i]);
auto it=s.lower_bound(a[i]);
if(it!=s.begin()) l[i]=*(--it);
}
s.clear();
for(int i=n;i>=1;--i)
{
if(i+k+1<=n) s.erase(a[i+k+1]);
s.insert(a[i]);
auto it=s.lower_bound(a[i]);
if(it!=s.begin()) r[i]=*(--it);
}
for(int i=1;i<=n;++i)
{
int p=pos[i];
int x=max(l[p],r[p]);
ans[i]=ans[x]+1;
}
for(int i=1;i<=n;++i)
printf("%d%c",ans[i],i==n?'\n':' ');
}
return 0;
}
线段树
#include <bits/stdc++.h>
#define ls (rt<<1)
#define rs (rt<<1|1)
#define fi first
#define se second
#define ll long long
using namespace std;
const int maxn=1e5+10;
int t,n,k;
int a[maxn],pos[maxn],ans[maxn];
int st[maxn<<2];
void update(int rt,int p,int L,int R)
{
if(L==R)
{
st[rt]=a[p];
return;
}
int mid=(L+R)>>1;
if(p<=mid) update(ls,p,L,mid);
if(p>mid) update(rs,p,mid+1,R);
st[rt]=max(st[ls],st[rs]);
}
int query(int rt,int l,int r,int L,int R)
{
if(l<=L&&R<=r) return st[rt];
int mid=(L+R)>>1;
int ans=0;
if(l<=mid) ans=max(ans,query(ls,l,r,L,mid));
if(r>mid) ans=max(ans,query(rs,l,r,mid+1,R));
return ans;
}
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;++i) scanf("%d",&a[i]),pos[a[i]]=i;
memset(ans,0,sizeof(ans));
memset(st,0,sizeof(st));
for(int i=1;i<=n;++i)
{
int l=max(pos[i]-k,1);
int r=min(pos[i]+k,n);
int x=query(1,l,r,1,n);
ans[i]=ans[x]+1;
update(1,pos[i],1,n);
}
for(int i=1;i<=n;++i)
printf("%d%c",ans[i],i==n?'\n':' ');
}
return 0;
}
主席树
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e5+10;
int t,n,k;
int a[maxn],ans[maxn],pos[maxn];
int root[maxn],ls[maxn*40],rs[maxn*40],st[maxn*40],no;
int build(int L,int R)
{
int rt=++no;
if(L==R) return rt;
int mid=(L+R)>>1;
ls[rt]=build(L,mid);
rs[rt]=build(mid+1,R);
return rt;
}
int update(int pre,int p,int L,int R)
{
int rt=++no;
st[rt]=st[pre]+1;
ls[rt]=ls[pre];
rs[rt]=rs[pre];
if(L==R) return rt;
int mid=(L+R)>>1;
if(p<=mid) ls[rt]=update(ls[pre],p,L,mid);
if(p>mid) rs[rt]=update(rs[pre],p,mid+1,R);
return rt;
}
int query(int pre,int now,int p,int L,int R)
{
if(st[now]-st[pre]==0) return 0;
if(L==R) return L<=p-1?L:0;
int mid=(L+R)>>1;
if(p-1<=mid||st[rs[now]]-st[rs[pre]]==0)
return query(ls[pre],ls[now],p,L,mid);
int res=query(rs[pre],rs[now],p,mid+1,R);
if(res!=0) return res;
return query(ls[pre],ls[now],p,L,mid);
}
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;++i) scanf("%d",&a[i]),pos[a[i]]=i;
no=0;
memset(ans,0,sizeof(ans));
root[0]=build(1,n);
for(int i=1;i<=n;++i)
root[i]=update(root[i-1],a[i],1,n);
for(int i=1;i<=n;++i)
{
int l=max(1,pos[i]-k);
int r=min(n,pos[i]+k);
int x=query(root[l-1],root[r],i,1,n);
ans[i]=ans[x]+1;
}
for(int i=1;i<=n;++i)
printf("%d%c",ans[i],i==n?'\n':' ');
}
return 0;
}
array HDU - 6703

链接:http://acm.hdu.edu.cn/showproblem.php?pid=6703
题意:给定一个 n n n 的排列,有两种操作,一是 a p o s + 1 e 7 a_{pos}+1e7 apos+1e7,二是找不等于 a i ( 1 ≤ i ≤ r ) a_i(1\le i\le r) ai(1≤i≤r) 的最小的大于等于 k 的数。
思路:
- 主席树:在区间 [ r + 1 , n ] [r+1,n] [r+1,n] 上找一个最小的 ≥ k \ge k ≥k的数,同时通过操作 1,相当于把原来的 a i a_i ai 删去了,那么那些被删去的 a i a_i ai 也是可选的
细节:set中维护删去的数,同时 n + 1也是可选的
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e5+10,inf=1e7;
int t,n,m;
int a[maxn];
int root[maxn],ls[maxn*40],rs[maxn*40],st[maxn*40],no;
int build(int L,int R)
{
int rt=++no;
if(L==R) return rt;
int mid=(L+R)>>1;
ls[rt]=build(L,mid);
rs[rt]=build(mid+1,R);
return rt;
}
int update(int pre,int p,int L,int R)
{
int rt=++no;
st[rt]=st[pre]+1;
ls[rt]=ls[pre];
rs[rt]=rs[pre];
if(L==R) return rt;
int mid=(L+R)>>1;
if(p<=mid) ls[rt]=update(ls[pre],p,L,mid);
if(p>mid) rs[rt]=update(rs[pre],p,mid+1,R);
return rt;
}
int query(int pre,int now,int p,int L,int R)
{
if(st[now]-st[pre]==0) return inf;
if(L==R) return L>=p?L:inf;
int mid=(L+R)>>1;
if(p>=mid+1||st[ls[now]]-st[ls[pre]]==0)
return query(rs[pre],rs[now],p,mid+1,R);
int res=query(ls[pre],ls[now],p,L,mid);
if(res!=inf) return res;
return query(rs[pre],rs[now],p,mid+1,R);
}
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
no=0;
root[0]=build(1,n);
for(int i=1;i<=n;++i)
root[i]=update(root[i-1],a[i],1,n);
int op,t1,t2,t3,pos,r,k,ans=0;
set<int> s;
s.insert(n+1);
while(m--)
{
scanf("%d",&op);
if(op==1)
{
scanf("%d",&t1);
pos=ans^t1;
s.insert(a[pos]);
}
else
{
scanf("%d%d",&t2,&t3);
r=t2^ans;
k=t3^ans;
ans=query(root[r],root[n],k,1,n);
auto it=s.lower_bound(k);
if(it!=s.end())
ans=min(ans,*it);
printf("%d\n",ans);
}
}
}
return 0;
}
H Cutting Bamboos 2019牛客暑期多校训练营(第九场)

链接:https://ac.nowcoder.com/acm/contest/889/H
题意:给定长度为 n 的数组,每个 a i a_i ai 代表竹子的长度,给定询问 (l,r,x,y) ,将 [ l , r ] [l,r] [l,r] 的竹子从水平方向砍 y 次,每次砍掉的竹子总长度相同,问砍第 x 次时的高度是多少
思路:关键在于在主席树上查找大于等于 p 的全部竹子
#include <bits/stdc++.h>
#define fi first
#define se second
#define ll long long
#define pll pair<ll,ll>
using namespace std;
const int maxn=2e5+10,inf=1e7;
const double eps=1e-8;
int n,q;
int a[maxn];
ll pref[maxn];
int l,r,x,y;
int root[maxn],ls[maxn*40],rs[maxn*40],no;
vector<int> allx;
struct Segment
{
int cnt;
ll sum;
}st[maxn*40];
int build(int L,int R)
{
int rt=++no;
st[rt].cnt=0;
st[rt].sum=0;
if(L==R) return rt;
int mid=(L+R)>>1;
ls[rt]=build(L,mid);
rs[rt]=build(mid+1,R);
return rt;
}
int update(int pre,int p,int L,int R)
{
int rt=++no;
st[rt].cnt=st[pre].cnt+1;
st[rt].sum=st[pre].sum+allx[p-1];
ls[rt]=ls[pre];
rs[rt]=rs[pre];
if(L==R) return rt;
int mid=(L+R)>>1;
if(p<=mid) ls[rt]=update(ls[pre],p,L,mid);
if(p>mid) rs[rt]=update(rs[pre],p,mid+1,R);
return rt;
}
pll query(int pre,int now,int p,int L,int R)
{
if(L==R) return {st[now].cnt-st[pre].cnt,st[now].sum-st[pre].sum};
int mid=(L+R)>>1;
if(p<=mid)
{
pll ans=query(ls[pre],ls[now],p,L,mid);
ans.fi+=st[rs[now]].cnt-st[rs[pre]].cnt;
ans.se+=st[rs[now]].sum-st[rs[pre]].sum;
return ans;
}
else return query(rs[pre],rs[now],p,mid+1,R);
}
pll query2(int pre,int now,int l,int r,int L,int R)
{
if(l<=L&&R<=r)
return {st[now].cnt-st[pre].cnt,st[now].sum-st[pre].sum};
int mid=(L+R)>>1;
pll ans1={0,0},ans2={0,0};
if(l<=mid)
ans1=query2(ls[pre],ls[now],l,r,L,mid);
if(r>mid)
ans2=query2(rs[pre],rs[now],l,r,mid+1,R);
return {ans1.fi+ans2.fi,ans1.se+ans2.se};
}
int main()
{
scanf("%d%d",&n,&q);
for(int i=1;i<=n;++i)
{
scanf("%d",&a[i]);
pref[i]=pref[i-1]+a[i];
allx.push_back(a[i]);
}
sort(allx.begin(),allx.end());
allx.resize(unique(allx.begin(),allx.end())-allx.begin());
int tot=allx.size();
root[0]=build(1,tot);
for(int i=1;i<=n;++i)
{
int p=lower_bound(allx.begin(),allx.end(),a[i])-allx.begin()+1;
root[i]=update(root[i-1],p,1,tot);
}
while(q--)
{
scanf("%d%d%d%d",&l,&r,&x,&y);
double L=0,R=allx.back();
double sum=pref[r]-pref[l-1];
double tar=sum/(1.0*y)*x;
while(L+eps<=R)
{
double mid=(L+R)/2;
int p=upper_bound(allx.begin(),allx.end(),mid)-allx.begin()+1;
pll res=query2(root[l-1],root[r],p,tot,1,tot);
if(res.se-res.fi*mid>=tar) L=mid;
else R=mid;
}
cout<<setprecision(8)<<fixed<<L<<"\n";
}
return 0;
}
E. Find the median 2019牛客第七场 (线段树)
题意:每次在集合中加入 [ l i , r i ] [l_i,r_i] [li,ri] 中的数后,查询中位数


思路:离散化之后区间更新到线段树上,然后找第 k个数即可。全部开long long,就可以过了
#include <bits/stdc++.h>
#define fi first
#define se second
#define ls (rt<<1)
#define rs (rt<<1|1)
#define ll long long
#define int ll
using namespace std;
const int maxn=4e5+10;
int n;
int X1,X2,A1,B1,C1,M1;
int Y1,Y2,A2,B2,C2,M2;
int l[maxn],r[maxn],x[maxn],y[maxn];
vector<int> allx;
ll st[maxn<<3],lazy[maxn<<3];
void pushDown(int rt,int L,int R)
{
if(lazy[rt])
{
int mid=(L+R)>>1;
st[ls]+=(allx[mid]-allx[L-1])*lazy[rt];
st[rs]+=(allx[R]-allx[mid])*lazy[rt];
lazy[ls]+=lazy[rt];
lazy[rs]+=lazy[rt];
lazy[rt]=0;
}
}
void pushUp(int rt)
{
st[rt]=st[ls]+st[rs];
}
void update(int rt,int l,int r,int L,int R)
{
if(l<=L&&R<=r)
{
st[rt]+=allx[R]-allx[L-1];
lazy[rt]+=1;
return;
}
pushDown(rt,L,R);
int mid=(L+R)>>1;
if(l<=mid) update(ls,l,r,L,mid);
if(r>mid) update(rs,l,r,mid+1,R);
pushUp(rt);
}
int query(int rt,int k,int L,int R)
{
if(L==R)
{
int x=st[rt]/(allx[L]-allx[L-1]);
return allx[L-1]+k/x+(k%x?1:0);
}
pushDown(rt,L,R);
int mid=(L+R)>>1;
if(k<=st[ls]) return query(ls,k,L,mid);
else return query(rs,k-st[ls],mid+1,R);
}
main()
{
scanf("%lld",&n);
scanf("%lld%lld%lld%lld%lld%lld",&X1,&X2,&A1,&B1,&C1,&M1);
scanf("%lld%lld%lld%lld%lld%lld",&Y1,&Y2,&A2,&B2,&C2,&M2);
x[1]=X1,x[2]=X2;
y[1]=Y1,y[2]=Y2;
for(int i=3;i<=n;++i)
x[i]=(1ll*A1*x[i-1]+1ll*B1*x[i-2]+C1)%M1;
for(int i=3;i<=n;++i)
y[i]=(1ll*A2*y[i-1]+1ll*B2*y[i-2]+C2)%M2;
for(int i=1;i<=n;++i)
{
int a=min(x[i],y[i])+1;
int b=max(x[i],y[i])+1;
allx.push_back(a-1);
allx.push_back(b);
l[i]=a-1,r[i]=b;
}
sort(allx.begin(),allx.end());
allx.resize(unique(allx.begin(),allx.end())-allx.begin());
int tot=allx.size()-1;
ll sum=0;
for(int i=1;i<=n;++i)
{
sum+=r[i]-l[i];
int p1=lower_bound(allx.begin(),allx.end(),l[i])-allx.begin()+1;
int p2=lower_bound(allx.begin(),allx.end(),r[i])-allx.begin();
update(1,p1,p2,1,tot);
printf("%lld\n",query(1,(sum+1)/2,1,tot));
}
}