uva1069 - Always an integer
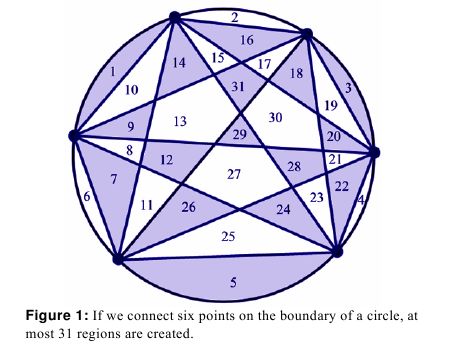
Combinatorics is a branch of mathematics chiefly concerned with counting discrete objects. For instance, how many ways can you pick two people out of a crowd of n people? Into how many regions can you divide a circular disk by connecting n points on its boundary with one another? How many cubes are in a pyramid with square layers ranging from 1×1 to n×n cubes?
Many questions like these have answers that can be reduced to simple polynomials in n. The answer to the first question above is n(n - 1)/2, or (n
2 - n)/2. The answer to the second is (n4 - 6n3 + 23n2 - 18n + 24)/24. The answer to the third is n(n + 1)(2n + 1)/6, or (2n3 + 3n2 + n)/6. We write these polynomials in a standard form, as a polynomial with integer coefficients divided by a positive integer denominator.
These polynomials are answers to questions that can have integer answers only. But since they have fractional coefficients, they look as if they could produce non-integer results! Of course, evaluating these particular polynomials on a positive integer always results in an integer. For other polynomials of similar form, this is not necessarily true. It can be hard to tell the two cases apart. So that, naturally, is your task.
Input
The input consists of multiple test cases, each on a separate line. Each test case is an expression in the form (P)/D, where P is a polynomial with integer coefficients and D is a positive integer denominator. P is a sum of terms of the form CnE, where the coefficient C and the exponent E satisfy the following conditions:
- E is an integer satisfying 0
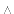E100. If E is 0, then CnE is expressed as C. If E is 1, then Cn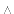E is expressed as Cn, unless C is 1 or -1. In those instances, Cn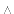E is expressed as n or - n. - C is an integer. If C is 1 or -1 and E is not 0 or 1, then the Cn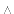E will appear as n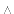E or - n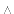E.
- Only non-negative C values that are not part of the first term in the polynomial are preceded by +.
- Exponents in consecutive terms are strictly decreasing.
- C and D fit in a 32-bit signed integer.
See the sample input for details.
Input is terminated by a line containing a single period.
Output
For each test case, print the case number (starting with 1). Then print `Always an integer' if the test case polynomial evaluates to an integer for every positive integer n. Print `Not always an integer' otherwise. Print the output for separate test cases on separate lines. Your output should follow the same format as the sample output.
Sample Input
(n^2-n)/2 (2n^3+3n^2+n)/6 (-n^14-11n+1)/3 .
Sample Output
Case 1: Always an integer Case 2: Always an integer Case 3: Not always an integer
给你一个多项式，问n取任何值的时候这个多项式的值是否都是整数。
设最高项数为k。当k=0时，不存在n，只要计算P（1）是否为整数。当k=1时，设P（n）=a*n+b，P（n+1）-P（n）=a，是等差数列，只要首项和公差都是D的倍数，n取任何值P都是d的倍数，也就是只要P（1）和P（2）是D的倍数就行。当k=3时，设P（n）=a*n^2+b*n+c，P（n+1）-P（n）=2an+a+b，因为2an+a+b是n的一次多项式，只有当n=1和n=2时都是D的倍数的时候2an+a+b才能被D整除，也就是P(1),P(2)-P(1),P(3)-P(2)都要是D的倍数，因此只要满足P(1),P(2),P(3)都是D的倍数就行。
根据数学归纳法，只要n的取值从1...k+1的P(n)都是D的倍数，n取任何值都会是D的倍数。
训练指南上还有个差分数列的图，写的非常清楚。。
我用数据结构里面那个表达式求值的方法写的，代码略坑，还有就是昨天数据结构考的跟翔一样
#include
#include
#include
#include
#include
#include
#include