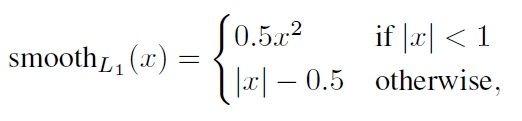SSD算法分析
SSD算法分析
- 1 SSD算法概述
- 2 SSD整体流程
- 3 SSD中的重要概念
- 3.1 多尺度Feature Map检测
- 3.2 Default Box
- 3.2.1 设计思路
- 3.2.2 参数计算
- 4 SSD网络架构与网络预测
- 4.1 网络架构
- 4.2 网络预测
- 4.3 预测值解码
- 5 网络训练
- 5.1 Ground Truth编码
- 5.2 匹配策略
- 5.3 损失函数
- 5.3.1 定位损失
- 5.3.2 分类损失
SSD论文地址:https://arxiv.org/abs/1512.02325
1 SSD算法概述
SSD由WeiLiu大神提出,英文全称Single Shot MultiBox Detector属于One Stage算法。SSD的核心是使用小的卷积核(filter)在特征图(feature map)上预测类别以及边界框的偏移量。SSD算法在速度和精度上都比YOLOv1好很多,且精度可以与Faster RCNN相媲美。
2 SSD整体流程
如图 2-1 为SSD算法的整体流程,输入一张 300 × 300 300\times300 300×300的图片;图片经过SSD特征提取网络的卷积运算生成一系列feature map,SSD选择其中的6个(图中用蓝色矩形框标出)作为“有效特征层”。接下来SSD对”有效特征层“进行卷积运算获得目标的位置信息与类别信息并将各个”有效特征层“获得的信息合并;最后使用非极大值抑制法(NMS)筛选出最终的检测结果。
3 SSD中的重要概念
3.1 多尺度Feature Map检测
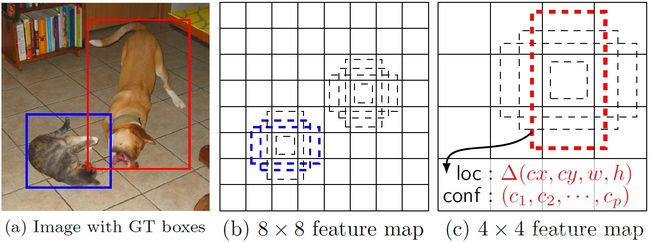
图像在进行卷积运算时,生成的feature map与原图相比具有空间位置的不变性;如果卷积运算生成的feature map形状为 m × n m \times n m×n则相当于将原图片划分成 m × n m \times n m×n个网格。如图3- 所示。因此,SSD的6个“有效特征层”分别相当于将原图片划分为 38 × 38 38\times 38 38×38, 19 × 19 19\times 19 19×19, 10 × 10 10\times 10 10×10, 5 × 5 5\times 5 5×5, 3 × 3 3\times 3 3×3和 1 × 1 1\times 1 1×1。
回顾目标检测原理,如果物体落在feature map的某一个网格中则该网格(或该网格中的一组Anchor Box)负责对该物体进行检测。直观上能够理解SSD的多尺度检测原理,SSD使用不同形状的feature map检测不同尺寸的物体, 38 × 38 38\times 38 38×38的负责检测小物体 3 × 3 3\times 3 3×3的负责检测大物体。图片在卷积神经网络中进行运算的过程中,随着网络层数的加深小物体的信息往往会丢失;因此SSD使用前端网络的feature map检测小物体后端的网络检测大物体。
多尺度Feature Map检测是SSD的特色,也是其比YOLOv1精度更高也更擅长检测小物体的重要原因。
3.2 Default Box
SSD借鉴Faster RCNN中Anchor Box的理念提出了类似的Default Box(也称Prior Box本文对二者混合使用不加区分)。
3.2.1 设计思路
如图3-1所示,SSD在各个“有效特征层”的每一个网格上设置了一组尺度和长宽比不同的Default Box以匹配不同尺寸和形状的物体;例如图3-1(a)中cat尺寸较小且形状类似正方形适合由用图(b)中 8 × 8 8\times 8 8×8的feature map的蓝色Default Box负责,而dog的尺寸较大且形状细长适合使用图(b)中 4 × 4 4\times 4 4×4的feature map中的红色Default Box来预测。SSD的网络预测值实际上就是每个Default Box的调整情况,有Default Box作为预测的基准在一定程度上减少了模型训练的难度。
参照图 2-1, 19 × 19 19\times 19 19×19的“有效特征层”每个网格上设置了4个Default Box整个feature map就有 19 × 19 × 4 = 2166 19\times 19\times 4=2166 19×19×4=2166个Default Box;依次类推整个SSD网络共有8732个Default Box。
3.2.2 参数计算
SSD每个“有效特征层”各自的每个网格包含的Default Box具有尺寸和宽高比,在实现时我们只需要计算出一组Default Box的参数之后在每个网格上复制即可。计算机表示一个物体的位置时,需要知道物体的中心点坐标及其长度宽度;每个Default Box的中心就是其所在网格的中心,需要确定的参数只有尺度和宽高比。Default Box的尺度遵守一个线性递增规则:随着feature map大小降低,Default Box尺度线性增加;第k个“有效特征层”的Default Box尺度计算公式为: S k = S m i n + S m a x − S m i n m − 1 ( k − 1 ) , k ∈ [ 1 , m ] S_k= S_{min} + \frac {S_{max}-S_{min} } {m-1}(k-1),k∈[1,m] Sk=Smin+m−1Smax−Smin(k−1),k∈[1,m] 其中m为“有效特征层”个数但其取值为5;因为第一个“有效特征层”(conv4-3)的尺度是单独设置的。 S k S_k Sk的含义为第k个“有效特征层”的Default Box的大小相对于图片的比例,SSD论文中取 S m i n = 0.2 S m a x = 0.9 S_{min}=0.2S_{max}=0.9 Smin=0.2Smax=0.9。第一个“有效特征层”的尺度一般设置为 S m i n 2 = 0.1 \frac {S_{min}} 2=0.1 2Smin=0.1。参考SSD源码与一些优秀up主的代码,在计算 S k S_k Sk时一般不直接使用上面的公式;而是将每个 S k S_k Sk的尺度放大100倍,此时 S k S_k Sk的增长步长为 ⌊ ⌊ S m a x × 100 ⌋ − ⌊ S m i n × 100 ⌋ m − 1 ⌋ = 17 \lfloor \frac {{\lfloor S_{max} \times 100 \rfloor}-{\lfloor S_{min} \times 100 \rfloor}} {m-1}\rfloor =17 ⌊m−1⌊Smax×100⌋−⌊Smin×100⌋⌋=17;代入数值计算可得放大后的 S k S_k Sk分别为20、37、54、71、88,再将数值除以100进行还原此时 S 1 S_1 S1— S 6 S_6 S6分别为0.2,0.37,0.54,0.71,0.88。对于Default Box的宽高比,一般选取 a r ∈ { 1 , 2 , 3 , 1 2 , 1 3 } a_r∈\{1,2,3,\frac 1 2,\frac 1 3\} ar∈{1,2,3,21,31}。对于各自的宽高比,按照如下公式计算其宽度和高度在图片中的比例: w k a = S k a r , h k a = S k / a r w_k^a=S_k\sqrt a_r ,h_k^a=S_k / \sqrt a_r wka=Skar,hka=Sk/ar。
默认情况下SSD的每个“有效特征层”会设置一个 a r = 1 a_r=1 ar=1且尺度为 S k S_k Sk的Default Box和一个 a r = 1 a_r=1 ar=1且尺度为 S k S k + 1 \sqrt {S_kS_{k+1}} SkSk+1的Default Box,即两个大小不同的正方形。对于最后一个“有效特征层”(第m个),需要补充一个虚拟尺度 S m + 1 = 88 + 17 100 = 1.05 S_{m+1}=\frac {88+17}{100}=1.05 Sm+1=10088+17=1.05来计算第二个正方形的尺寸比例。因此“有效特征层”的每个网格最多会有个Default Box,它们的宽高比分别为 { 1 , 2 , 3 , 1 2 , 1 3 , 1 ′ } \{1,2,3,\frac 1 2,\frac 1 3,1^{'}\} {1,2,3,21,31,1′}。有些“有效特征层”的网格中只包含个Default Box,不使用宽高比 3 3 3和 1 3 \frac 1 3 31。
得到所有“有效特征层”Default Box的尺寸和宽高比后我们需要将其换算为实际尺寸(像素值);由前文可知,我们只需要确定“有效特征层”的每个网格中两个正方形Default Box的边长,其他长方形Default Box的宽高都可以由“小正方形”的边长换算得到。本文输入图片尺寸为 300 × 300 300\times 300 300×300,将Default Box尺寸比例 S k S_k Sk代入得到各个“有效特征层”的“小正方形”边长分别为30,60,111,162,213,264;将比例 S k + 1 ( 包 含 S m + 1 ) S_{k+1}(包含S_{m+1}) Sk+1(包含Sm+1)代入,得到各个“有效特征层”的“大正方形”边长分别为60,111,162,213,264,315。将各个”有效特征层“的”小正方形“、”大正方形“Default Box的尺寸整理为表3-1。
| 小正方形边长 | 大正方形边长 | |
|---|---|---|
| conv4_3 | 30 | 60 |
| conv4_3 | 60 | 111 |
| conv6_2 | 111 | 162 |
| conv7_2 | 162 | 213 |
| conv8_2 | 213 | 264 |
| conv9_2 | 264 | 315 |
4 SSD网络架构与网络预测
4.1 网络架构
图 4-1 为SSD的网络架构,SSD网络由经典图像分类网络VGG16修改得到(VGG16介绍);SSD网络对于VGG16的主要修改如下:
- 将原VGG网络的FC6、FC7替换为卷积层
- 去掉VGG网络的所有Dropout层和FC8
- 在VGG网络最后端新增Conv6、Conv7、Conv8、Conv9
图片传入SSD网络后,运算过程与feature map形状变化如下(卷积核步长stride默认为1):
- 图片输入后形状被强制调整为 300 × 300 × 3 300\times 300\times 3 300×300×3
- conv1:经过两个卷积核大小为 3 × 3 3\times 3 3×3卷积层,输出feature map形状为 300 × 300 × 64 300\times 300\times 64 300×300×64;再经过卷积核大小为 2 × 2 2\times 2 2×2的最大池化层,输出feature map形状为 150 × 150 × 64 150\times 150\times 64 150×150×64
- conv2:经过两个卷积核大小为 3 × 3 3\times 3 3×3卷积层,输出feature map形状为 150 × 150 × 128 150\times 150\times 128 150×150×128;再经过卷积核大小为 2 × 2 2\times 2 2×2的最大池化层,输出feature map形状为 75 × 75 × 128 75\times 75\times 128 75×75×128
- conv3:经过两个卷积核大小为 3 × 3 3\times 3 3×3卷积层,输出feature map形状为 75 × 75 × 256 75\times 75\times 256 75×75×256;再经过卷积核大小为 2 × 2 2\times 2 2×2的最大池化层,输出feature map形状为 38 × 38 × 256 38\times 38\times 256 38×38×256
- conv4:经过两个卷积核大小为 3 × 3 3\times 3 3×3卷积层,输出feature map形状为 38 × 38 × 512 38\times 38\times 512 38×38×512;再经过卷积核大小为 2 × 2 2\times 2 2×2的最大池化层,输出feature map形状为 19 × 19 × 512 19\times 19\times 512 19×19×512
- conv5:经过两个卷积核大小为 3 × 3 3\times 3 3×3卷积层,输出feature map形状为 19 × 19 × 512 19\times 19\times 512 19×19×512;再经过卷积核大小为 2 × 2 2\times 2 2×2的最大池化层,输出feature map形状为 19 × 19 × 512 19\times 19\times 512 19×19×512
- fc6与fc7:经过两个卷积核大小为 3 × 3 3\times 3 3×3卷积层,输出feature map形状为 19 × 19 × 1024 19\times 19\times 1024 19×19×1024(fc6、fc7在原网络中为全连接层)
- conv6:经过一个卷积核大小为 1 × 1 1\times 1 1×1卷积层,输出feature map形状为 19 × 19 × 256 19\times 19\times 256 19×19×256;再经过卷积核大小为 3 × 3 3\times 3 3×3步长为2的卷积层,输出feature map形状为 10 × 10 × 512 10\times 10\times 512 10×10×512
- conv7:经过一个卷积核大小为 1 × 1 1\times 1 1×1卷积层,输出feature map形状为 10 × 10 × 128 10\times 10\times 128 10×10×128;再经过卷积核大小为 3 × 3 3\times 3 3×3步长为2的卷积层,输出feature map形状为 5 × 5 × 256 5\times 5\times 256 5×5×256
- conv8:经过一个卷积核大小为 1 × 1 1\times 1 1×1卷积层,输出feature map形状为 5 × 5 × 128 5\times 5\times 128 5×5×128;再经过卷积核大小为 3 × 3 3\times 3 3×3的卷积层,输出feature map形状为 3 × 3 × 256 3\times 3\times 256 3×3×256
- conv9:经过一个卷积核大小为 1 × 1 1\times 1 1×1卷积层,输出feature map形状为 3 × 3 × 128 3\times 3\times 128 3×3×128;再经过卷积核大小为 3 × 3 3\times 3 3×3的卷积层,输出feature map形状为 1 × 1 × 256 1\times 1\times 256 1×1×256
""" 结合GitHub上pierluigiferrari/ssd_keras/keras_ssd300.py对kuhung/SSD_keras/ssd.py的网络实现代码做简单修改"""
"""韩伟奇于2020年4月"""
import keras.backend as K
from keras.layers import Activation
from keras.layers import Conv2D
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers import GlobalAveragePooling2D
from keras.layers import Input
from keras.layers import MaxPooling2D
from keras.layers import merge, concatenate
from keras.layers import Reshape
from keras.layers import ZeroPadding2D
from keras.models import Model
def VGG16(input_tensor):
# SSD结构,net字典;SSD网络由VGG网络改变得到
net = {}
# Block 1
net['input'] = input_tensor
# Feature map形状变化: 300,300,3 -> 150,150,64
net['conv1_1'] = Conv2D(64, kernel_size=(3,3),
activation='relu',
padding='same',
name='conv1_1')(net['input'])
net['conv1_2'] = Conv2D(64, kernel_size=(3,3),
activation='relu',
padding='same',
name='conv1_2')(net['conv1_1'])
net['pool1'] = MaxPooling2D((2, 2), strides=(2, 2), padding='same',
name='pool1')(net['conv1_2'])
# Block 2
# Feature map形状变化: 150,150,64 -> 75,75,128
net['conv2_1'] = Conv2D(128, kernel_size=(3,3),
activation='relu',
padding='same',
name='conv2_1')(net['pool1'])
net['conv2_2'] = Conv2D(128, kernel_size=(3,3),
activation='relu',
padding='same',
name='conv2_2')(net['conv2_1'])
net['pool2'] = MaxPooling2D((2, 2), strides=(2, 2), padding='same',
name='pool2')(net['conv2_2'])
# Block 3
# Feature map形状变化: 75,75,128 -> 38,38,256
net['conv3_1'] = Conv2D(256, kernel_size=(3,3),
activation='relu',
padding='same',
name='conv3_1')(net['pool2'])
net['conv3_2'] = Conv2D(256, kernel_size=(3,3),
activation='relu',
padding='same',
name='conv3_2')(net['conv3_1'])
net['conv3_3'] = Conv2D(256, kernel_size=(3,3),
activation='relu',
padding='same',
name='conv3_3')(net['conv3_2'])
net['pool3'] = MaxPooling2D((2, 2), strides=(2, 2), padding='same',
name='pool3')(net['conv3_3'])
# Block 4
# Feature map形状变化: 38,38,256 -> 19,19,512
net['conv4_1'] = Conv2D(512, kernel_size=(3,3),
activation='relu',
padding='same',
name='conv4_1')(net['pool3'])
net['conv4_2'] = Conv2D(512, kernel_size=(3,3),
activation='relu',
padding='same',
name='conv4_2')(net['conv4_1'])
net['conv4_3'] = Conv2D(512, kernel_size=(3,3),
activation='relu',
padding='same',
name='conv4_3')(net['conv4_2'])
net['pool4'] = MaxPooling2D((2, 2), strides=(2, 2), padding='same',
name='pool4')(net['conv4_3'])
# Block 5
# Feature map形状变化: 19,19,512 -> 19,19,512
net['conv5_1'] = Conv2D(512, kernel_size=(3,3),
activation='relu',
padding='same',
name='conv5_1')(net['pool4'])
net['conv5_2'] = Conv2D(512, kernel_size=(3,3),
activation='relu',
padding='same',
name='conv5_2')(net['conv5_1'])
net['conv5_3'] = Conv2D(512, kernel_size=(3,3),
activation='relu',
padding='same',
name='conv5_3')(net['conv5_2'])
net['pool5'] = MaxPooling2D((3, 3), strides=(1, 1), padding='same',
name='pool5')(net['conv5_3'])
# FC6
# Feature map形状变化: 19,19,512 -> 19,19,1024
net['fc6'] = Conv2D(1024, kernel_size=(3,3), dilation_rate=(6, 6),
activation='relu', padding='same',
name='fc6')(net['pool5'])
# FC7
# Feature map形状变化: 19,19,1024 -> 19,19,1024
net['fc7'] = Conv2D(1024, kernel_size=(1,1), activation='relu',
padding='same', name='fc7')(net['fc6'])
# Block 6
# Feature map形状变化: 19,19,512 -> 10,10,512
net['conv6_1'] = Conv2D(256, kernel_size=(1,1), activation='relu',
padding='same',
name='conv6_1')(net['fc7'])
net['conv6_2'] = ZeroPadding2D(padding=((1, 1), (1, 1)), name='conv6_padding')(net['conv6_1'])
net['conv6_2'] = Conv2D(512, kernel_size=(3,3), strides=(2, 2),
activation='relu',
name='conv6_2')(net['conv6_2'])
# Block 7
# Feature map形状变化: 10,10,512 -> 5,5,256
net['conv7_1'] = Conv2D(128, kernel_size=(1,1), activation='relu',
padding='same',
name='conv7_1')(net['conv6_2'])
net['conv7_2'] = ZeroPadding2D(padding=((1, 1), (1, 1)), name='conv7_padding')(net['conv7_1'])
net['conv7_2'] = Conv2D(256, kernel_size=(3,3), strides=(2, 2),
activation='relu', padding='valid',
name='conv7_2')(net['conv7_2'])
# Block 8
# Feature map形状变化: 5,5,256 -> 3,3,256
net['conv8_1'] = Conv2D(128, kernel_size=(1,1), activation='relu',
padding='same',
name='conv8_1')(net['conv7_2'])
net['conv8_2'] = Conv2D(256, kernel_size=(3,3), strides=(1, 1),
activation='relu', padding='valid',
name='conv8_2')(net['conv8_1'])
# Block 9
# Feature map形状变化: 3,3,256 -> 1,1,256
net['conv9_1'] = Conv2D(128, kernel_size=(1,1), activation='relu',
padding='same',
name='conv9_1')(net['conv8_2'])
net['conv9_2'] = Conv2D(256, kernel_size=(3,3), strides=(1, 1),
activation='relu', padding='valid',
name='conv9_2')(net['conv9_1'])
return net
4.2 网络预测
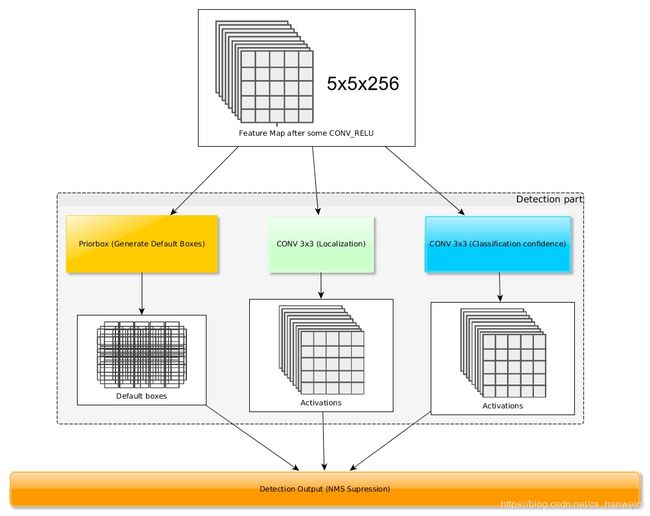
参照图4-2,SSD在网络架构中选取conv4_3生成的feature map、fc7的feature map、conv6_2的feature map、conv7_2的feature map、conv8_2的feature map、conv9_2生成的feature map作为”有效特征层“来预测结果。获得"有效特征层"后,SSD使用卷积操作获取物体的位置信息与类别信息。针对每个"有效特征层",分别使用通道数为num_prior × 4 \times 4 ×4和num_prior × \times ×num_classes的 3 × 3 3\times 3 3×3卷积核进行卷积运算。其中,num_prior 为"有效特征层"每个网格中Prior Box(Default Box)的数量;回顾目标检测原理中的物体位置表示方法,SSD通过调整Prior Box位置和形状来表示检测到的物体,通道数为num_priors x 4的卷积操作获得的是Prior Box的调整情况:
(Prior Box中心点x坐标调整情况,Prior Box中心点y坐标调整情况,Prior Box宽度w调整情况,Prior Box高度h调整情况);
num_classes表示待检测的物体种类数量,通道数为num_priors × \times × num_classes的卷积 用于预测 “有效特征层”上 每一个网格点中每个Prior Box对应的物体种类;卷积运算的结果是每个Prior Box对于num_classes个物体类别各自的类别置信度。
对"有效特征层"进行卷积操作获得检测结果代码如下:
import keras.backend as K
from keras.layers import Activation
#from keras.layers import AtrousConvolution2D
from keras.layers import Conv2D
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers import GlobalAveragePooling2D
from keras.layers import Input
from keras.layers import MaxPooling2D
from keras.layers import merge, concatenate
from keras.layers import Reshape
from keras.layers import ZeroPadding2D
from keras.models import Model
from ssd_nets.VGG16 import VGG16
from ssd_nets.ssd_layers import Normalize
from ssd_nets.ssd_layers import PriorBox
def SSD300(input_shape, num_classes=21):
# 300,300,3
input_tensor = Input(shape=input_shape)
img_size = (input_shape[1], input_shape[0])
# SSD结构,net字典
net = VGG16(input_tensor)
#-----------------------对"有效特征层"进行卷积运算获得检测结果---------------------------#
# 对conv4_3进行处理 38,38,512
net['conv4_3_norm'] = Normalize(20, name='conv4_3_norm')(net['conv4_3']) #对网络进行Normalize操作
num_priors = 4 #conv4_3每个网格有4个Prior Box
# 预测框的处理
# 对"有效特征层"进行通道数为(num_prior*4)的卷积运算获得物体位置信息(Prior Box的调整情况) num_priors表示每个网格点先验框的数量,4表示对Prior Box的中心点x坐标,中心点y坐标,宽度w,高度h的调整情况
net['conv4_3_norm_mbox_loc'] = Conv2D(num_priors * 4, kernel_size=(3,3), padding='same', name='conv4_3_norm_mbox_loc')(net['conv4_3_norm']) #(38,38,512) -> (38,38,4*4)
net['conv4_3_norm_mbox_loc_flat'] = Flatten(name='conv4_3_norm_mbox_loc_flat')(net['conv4_3_norm_mbox_loc']) #Flatten为"压平"操作 (38,38,16) -> (23104)
# 对"有效特征层"进行通道数为(num_prior*num_classes)的卷积运算获得物体类别信息(物体属于各个类别的置信度) num_priors表示每个网格点先验框的数量,num_classes是所分的类
net['conv4_3_norm_mbox_conf'] = Conv2D(num_priors * num_classes, kernel_size=(3,3), padding='same',name='conv4_3_norm_mbox_conf')(net['conv4_3_norm']) #(38,38,512) -> (38,38,21*4)
net['conv4_3_norm_mbox_conf_flat'] = Flatten(name='conv4_3_norm_mbox_conf_flat')(net['conv4_3_norm_mbox_conf']) #(38,38,84) -> (121296)
priorbox = PriorBox(img_size, 30.0,max_size = 60.0, aspect_ratios=[2],
variances=[0.1, 0.1, 0.2, 0.2],
name='conv4_3_norm_mbox_priorbox')
net['conv4_3_norm_mbox_priorbox'] = priorbox(net['conv4_3_norm'])
# 对fc7层进行处理 19,19,1024
num_priors = 6 #fc7每个网格有6个Prior Box
net['fc7_mbox_loc'] = Conv2D(num_priors * 4, kernel_size=(3,3),padding='same',name='fc7_mbox_loc')(net['fc7']) #(19,19,1024) -> (19,19,6*4)
net['fc7_mbox_loc_flat'] = Flatten(name='fc7_mbox_loc_flat')(net['fc7_mbox_loc']) #(19,19,24) -> (8664)
net['fc7_mbox_conf'] = Conv2D(num_priors * num_classes, kernel_size=(3,3),padding='same',name='fc7_mbox_conf')(net['fc7']) #(19,19,1024) -> (19,19,6*21)
net['fc7_mbox_conf_flat'] = Flatten(name='fc7_mbox_conf_flat')(net['fc7_mbox_conf']) #(19,19,126) -> (45486)
priorbox = PriorBox(img_size, 60.0, max_size=111.0, aspect_ratios=[2, 3],
variances=[0.1, 0.1, 0.2, 0.2],
name='fc7_mbox_priorbox')
net['fc7_mbox_priorbox'] = priorbox(net['fc7'])
# 对conv6_2进行处理
num_priors = 6
x = Conv2D(num_priors * 4, kernel_size=(3,3), padding='same',name='conv6_2_mbox_loc')(net['conv6_2'])
net['conv6_2_mbox_loc'] = x
net['conv6_2_mbox_loc_flat'] = Flatten(name='conv6_2_mbox_loc_flat')(net['conv6_2_mbox_loc'])
x = Conv2D(num_priors * num_classes, kernel_size=(3,3), padding='same',name='conv6_2_mbox_conf')(net['conv6_2'])
net['conv6_2_mbox_conf'] = x
net['conv6_2_mbox_conf_flat'] = Flatten(name='conv6_2_mbox_conf_flat')(net['conv6_2_mbox_conf'])
priorbox = PriorBox(img_size, 111.0, max_size=162.0, aspect_ratios=[2, 3],
variances=[0.1, 0.1, 0.2, 0.2],
name='conv6_2_mbox_priorbox')
net['conv6_2_mbox_priorbox'] = priorbox(net['conv6_2'])
# 对conv7_2进行处理
num_priors = 6
x = Conv2D(num_priors * 4, kernel_size=(3,3), padding='same',name='conv7_2_mbox_loc')(net['conv7_2'])
net['conv7_2_mbox_loc'] = x
net['conv7_2_mbox_loc_flat'] = Flatten(name='conv7_2_mbox_loc_flat')(net['conv7_2_mbox_loc'])
x = Conv2D(num_priors * num_classes, kernel_size=(3,3), padding='same',name='conv7_2_mbox_conf')(net['conv7_2'])
net['conv7_2_mbox_conf'] = x
net['conv7_2_mbox_conf_flat'] = Flatten(name='conv7_2_mbox_conf_flat')(net['conv7_2_mbox_conf'])
priorbox = PriorBox(img_size, 162.0, max_size=213.0, aspect_ratios=[2, 3],
variances=[0.1, 0.1, 0.2, 0.2],
name='conv7_2_mbox_priorbox')
net['conv7_2_mbox_priorbox'] = priorbox(net['conv7_2'])
# 对conv8_2进行处理
num_priors = 4
x = Conv2D(num_priors * 4, kernel_size=(3,3), padding='same',name='conv8_2_mbox_loc')(net['conv8_2'])
net['conv8_2_mbox_loc'] = x
net['conv8_2_mbox_loc_flat'] = Flatten(name='conv8_2_mbox_loc_flat')(net['conv8_2_mbox_loc'])
x = Conv2D(num_priors * num_classes, kernel_size=(3,3), padding='same',name='conv8_2_mbox_conf')(net['conv8_2'])
net['conv8_2_mbox_conf'] = x
net['conv8_2_mbox_conf_flat'] = Flatten(name='conv8_2_mbox_conf_flat')(net['conv8_2_mbox_conf'])
priorbox = PriorBox(img_size, 213.0, max_size=264.0, aspect_ratios=[2],
variances=[0.1, 0.1, 0.2, 0.2],
name='conv8_2_mbox_priorbox')
net['conv8_2_mbox_priorbox'] = priorbox(net['conv8_2'])
# 对conv9_2进行处理
num_priors = 4
x = Conv2D(num_priors * 4, kernel_size=(3,3), padding='same',name='conv9_2_mbox_loc')(net['conv9_2'])
net['conv9_2_mbox_loc'] = x
net['conv9_2_mbox_loc_flat'] = Flatten(name='conv9_2_mbox_loc_flat')(net['conv9_2_mbox_loc'])
x = Conv2D(num_priors * num_classes, kernel_size=(3,3), padding='same',name='conv9_2_mbox_conf')(net['conv9_2'])
net['conv9_2_mbox_conf'] = x
net['conv9_2_mbox_conf_flat'] = Flatten(name='conv9_2_mbox_conf_flat')(net['conv9_2_mbox_conf'])
priorbox = PriorBox(img_size, 264.0, max_size=315.0, aspect_ratios=[2],
variances=[0.1, 0.1, 0.2, 0.2],
name='conv9_2_mbox_priorbox')
net['conv9_2_mbox_priorbox'] = priorbox(net['conv9_2'])
# 将所有结果进行堆叠
net['mbox_loc'] = concatenate([net['conv4_3_norm_mbox_loc_flat'], #(23104)
net['fc7_mbox_loc_flat'], #(8664)
net['conv6_2_mbox_loc_flat'], #(2400)
net['conv7_2_mbox_loc_flat'], #(600)
net['conv8_2_mbox_loc_flat'], #(144)
net['conv9_2_mbox_loc_flat']], #(16)
axis=1, name='mbox_loc') #共计34928
net['mbox_conf'] = concatenate([net['conv4_3_norm_mbox_conf_flat'],
net['fc7_mbox_conf_flat'],
net['conv6_2_mbox_conf_flat'],
net['conv7_2_mbox_conf_flat'],
net['conv8_2_mbox_conf_flat'],
net['conv9_2_mbox_conf_flat']],
axis=1, name='mbox_conf')
net['mbox_priorbox'] = concatenate([net['conv4_3_norm_mbox_priorbox'],
net['fc7_mbox_priorbox'],
net['conv6_2_mbox_priorbox'],
net['conv7_2_mbox_priorbox'],
net['conv8_2_mbox_priorbox'],
net['conv9_2_mbox_priorbox']],
axis=1, name='mbox_priorbox')
if hasattr(net['mbox_loc'], '_keras_shape'):
num_boxes = net['mbox_loc']._keras_shape[-1] // 4
elif hasattr(net['mbox_loc'], 'int_shape'):
num_boxes = K.int_shape(net['mbox_loc'])[-1] // 4
# 8732,4
net['mbox_loc'] = Reshape((num_boxes, 4),name='mbox_loc_final')(net['mbox_loc'])
# 8732,21
net['mbox_conf'] = Reshape((num_boxes, num_classes),name='mbox_conf_logits')(net['mbox_conf'])
net['mbox_conf'] = Activation('softmax',name='mbox_conf_final')(net['mbox_conf'])
net['predictions'] = concatenate([net['mbox_loc'],
net['mbox_conf'],
net['mbox_priorbox']],
axis=2, name='predictions')
print(net['predictions'])
model = Model(net['input'], net['predictions'])
return model
4.3 预测值解码
参照图 4-3 SSD通过对"有效特征层"进行卷积运算获得检测结果(Prior Box调整情况)后,需要结合预先设定的Prior Box将检测结果解码为物体的真实位置信息。SSD论文中定义bounding box(包围框)的编码方式为b=( b c x b_{cx} bcx, b c y b_{cy} bcy, b w b_{w} bw, b h b_{h} bh);Default Box的编码方式为d=( d c x d_{cx} dcx, d c y d_{cy} dcy, d w d_{w} dw, d h d_{h} dh);SSD输出的Default Box调整情况为 l l l=( l c x l_{cx} lcx, l c y l_{cy} lcy, l w l_{w} lw, l h l_{h} lh);参照SSD论文预测值 l l l的计算公式如下:
l c x = ( b c x − d c x ) / d w l c y = ( b c y − d c y ) / d h l w = l o g ( b w / d w ) , l h = l o g ( b h / d h ) l_{cx}=(b_{cx}-d_{cx})/d_{w} l_{cy}=(b_{cy}-d_{cy})/d_{h}\\ l_{w}=log(b_{w}/d_{w}) , l_{h}=log(b_{h}/d_{h}) lcx=(bcx−dcx)/dwlcy=(bcy−dcy)/dhlw=log(bw/dw),lh=log(bh/dh)
根据预测值 l l l的计算公式反向求解bounding box实际位置 b b b解码公式如下:
b c x = d w × l c x + d c x , b c y = d h × l c y + d c y b w = d w × e l w , b h = d h × e l h b_{cx}=d_{w}\times l_{cx}+d_{cx},b_{cy}=d_{h}\times l_{cy}+d_{cy}\\ b_{w}=d_{w} \times e^{l_w},b_{h}=d_{h} \times e^{l_h} bcx=dw×lcx+dcx,bcy=dh×lcy+dcybw=dw×elw,bh=dh×elh
解码获得的 b b b就是bounding box(预测框)的实际位置。
预测值解码实现代码:
def decode_boxes(self, mbox_loc, mbox_priorbox, variances):
"""
mbox_loc: prior box调整情况
mbox_priorbox: prior box 位置信息
variance: [0.1,0.1,0.2,0.2]
返回值 decode_bbox 为 8732个调整后的prior box的信息
"""
# 获得先验框的宽与高
prior_width = mbox_priorbox[:, 2] - mbox_priorbox[:, 0]
prior_height = mbox_priorbox[:, 3] - mbox_priorbox[:, 1]
# 获得先验框的中心点
prior_center_x = 0.5 * (mbox_priorbox[:, 2] + mbox_priorbox[:, 0])
prior_center_y = 0.5 * (mbox_priorbox[:, 3] + mbox_priorbox[:, 1])
# 真实框距离先验框中心的xy轴偏移情况
decode_bbox_center_x = mbox_loc[:, 0] * prior_width * variances[:, 0]
decode_bbox_center_x += prior_center_x
decode_bbox_center_y = mbox_loc[:, 1] * prior_height * variances[:, 1]
decode_bbox_center_y += prior_center_y
# 真实框的宽与高的求取
decode_bbox_width = np.exp(mbox_loc[:, 2] * variances[:, 2])
decode_bbox_width *= prior_width
decode_bbox_height = np.exp(mbox_loc[:, 3] * variances[:, 3])
decode_bbox_height *= prior_height
# 获取真实框的左上角与右下角
decode_bbox_xmin = decode_bbox_center_x - 0.5 * decode_bbox_width
decode_bbox_ymin = decode_bbox_center_y - 0.5 * decode_bbox_height
decode_bbox_xmax = decode_bbox_center_x + 0.5 * decode_bbox_width
decode_bbox_ymax = decode_bbox_center_y + 0.5 * decode_bbox_height
# 真实框的左上角与右下角进行堆叠
decode_bbox = np.concatenate((decode_bbox_xmin[:, None],
decode_bbox_ymin[:, None],
decode_bbox_xmax[:, None],
decode_bbox_ymax[:, None]), axis=-1)
# 防止超出0与1,将box限制在图片范围内
decode_bbox = np.minimum(np.maximum(decode_bbox, 0.0), 1.0)
return decode_bbox
解码后我们获得了8732个Prior Box的位置与类别信息,我们对其进行筛选获得最终的预测结果。首先每个Prior Box根据类别置信度确定其类别(置信度最大者)与置信度值,并过滤掉类别为背景的预测框。然后根据置信度阈值(如0.5)过滤掉置信度低于阈值的预测框。对于留下的预测框进行解码,根据Prior Box得到其真实的位置参数(解码后一般还需要做clip,防止预测框位置超出图片)。解码之后,一般需要根据置信度对预测框进行降序排列,然后仅保留置信度最大的top-k(如200)个预测框。最后就是进行NMS算法,过滤掉那些重叠度较大的预测框。最后剩余的预测框就是检测结果了。
筛选预测结果并输出的实现代码如下:
def detection_out(self, predictions, background_label_id=0, keep_top_k=200,
confidence_threshold=0.5):
"""
predictions 为网络预测输出 shape:(batch_size,8732,4+num_classes+prior box信息(4)+variance(4))
background_label_id 背景id默认为0
keep_top_k 保留置信度最高的预测框数量
confidence_threshold 置信度阈值
"""
# 位置检测结果(Prior Box调整情况)
mbox_loc = predictions[:, :, :4]
# 0.1,0.1,0.2,0.2
variances = predictions[:, :, -4:]
# Prior Box信息
mbox_priorbox = predictions[:, :, -8:-4]
# 置信度(Prior Box中每个类别的置信度)
mbox_conf = predictions[:, :, 4:-8]
results = []
# 对batch中的每一张图片进行处理
for i in range(len(mbox_loc)):
results.append([])
decode_bbox = self.decode_boxes(mbox_loc[i], mbox_priorbox[i], variances[i])
for c in range(self.num_classes):
if c == background_label_id:
continue
c_confs = mbox_conf[i, :, c]
c_confs_m = c_confs > confidence_threshold
if len(c_confs[c_confs_m]) > 0:
# 取出得分高于confidence_threshold的框
boxes_to_process = decode_bbox[c_confs_m]
confs_to_process = c_confs[c_confs_m]
# 进行iou的非极大抑制
feed_dict = {self.boxes: boxes_to_process,
self.scores: confs_to_process}
idx = self.sess.run(self.nms, feed_dict=feed_dict)
# 取出在非极大抑制中效果较好的内容
good_boxes = boxes_to_process[idx]
confs = confs_to_process[idx][:, None]
# 将label、置信度、框的位置进行堆叠。
labels = c * np.ones((len(idx), 1))
c_pred = np.concatenate((labels, confs, good_boxes),
axis=1)
# 添加进result里
results[-1].extend(c_pred)
if len(results[-1]) > 0:
# 按照置信度进行排序
results[-1] = np.array(results[-1])
argsort = np.argsort(results[-1][:, 1])[::-1]
results[-1] = results[-1][argsort]
# 选出置信度最大的keep_top_k个
results[-1] = results[-1][:keep_top_k]
return results
5 网络训练
5.1 Ground Truth编码
回顾4.2节,SSD网络的位置预测结果是Default Box的调整情况;对Default Box调整情况进行解码才能获得物体的真实位置信息;而Ground Truth(物体信息标签)中包含的是物体的真实位置信息(像素值)。然而,SSD的损失函数是是相对于网络的预测结果的;我们需要将物体的真实位置信息编码为Default Box的调整情况才能对网络参数进行训练。
参照4.3节,编码过程实际上就是解码过程的逆过程;这里约定Ground Truth编码方式为 g = ( g c x , g c y , g w , g h ) g=(g_{cx},g_{cy},g_{w},g_{h}) g=(gcx,gcy,gw,gh),Ground Truth编码值结果 g ^ = ( g ^ c x , g ^ c y , g ^ w , g ^ h ) \hat{g}=({\hat{g}_{cx},\hat{g}_{cy},\hat{g}_{w},\hat{g}_{h}}) g^=(g^cx,g^cy,g^w,g^h);Default Box编码方式为 d = ( d c x , d c y , d w , d h ) d=(d_{cx},d_{cy},d_{w},d_{h}) d=(dcx,dcy,dw,dh); g ^ \hat{g} g^编码公式为:
g ^ c x = ( g c x − d c x ) / d w , g ^ c y = ( g c y − d c y ) / d h g ^ w = l o g ( g w d w ) , g ^ h = l o g ( g h d h ) \hat{g}_{cx}=(g_{cx}-d_{cx})/d_w,\hat{g}_{cy}=(g_{cy}-d_{cy})/d_h\\ \hat{g}_{w}=log(\frac {g_w} {d_w}),\hat{g}_{h}=log(\frac {g_h} {d_h}) g^cx=(gcx−dcx)/dw,g^cy=(gcy−dcy)/dhg^w=log(dwgw),g^h=log(dhgh)
编码过程实现代码如下:
#编码实现代码(待插入)
5.2 匹配策略
在训练前,首先要确定训练图片中的Ground Truth(物体真实信息)与哪个Default Box来进行匹配,与之匹配的Default Box获得的调整情况将负责预测该物体。参照SSD论文,SSD的Default Box与Ground Truth的匹配原则主要有两条。首先,对于图片中每个Ground Truth,找到与其IOU最大的Default Box,该Default Box负责与其匹配,这样,可以保证每个Ground Truth一定与某个Default Box相匹配。通常称与Ground Truth匹配的Default Box为正样本,反之,若一个Default Box没有与任何Ground Truth进行匹配,那么该Default Box只能与背景匹配,就是负样本。通常一个图片中Ground Truth数量很少, 而Default Box却非常多,如果仅按第一个原则匹配,大多数Default Box都是负样本,正负样本极其不平衡,所以需要第二个原则。第二个原则是:对于剩余的未匹配Default Box,若某个Ground Truth与某个Default Box的 IOU大于某个阈值(例如0.5),那么该Default Box也与这个ground truth进行匹配。第二条原则意味着某个Ground Truth可能与多个Default Box相匹配,这是SSD允许的。但是反过来却不行,因为一个Default Box只能匹配一个Ground Truth,如果多个Ground Truth与某个Default Box 的IOU大于阈值,那么该Default Box只与IOU最大的那个Ground Truth进行匹配。
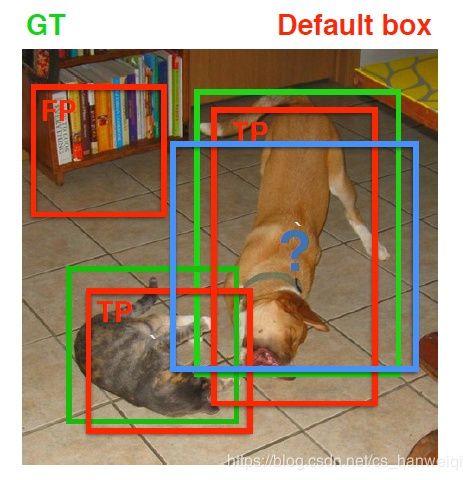
如图 5-1 所示,绿色框是Ground Truth,红色框为Default Box,TP表示正样本,FP表示负样本。包围dog的蓝框和红框与Ground Truth的IOU都大于阈值都是正样本,每个ground truth可以与多个Default Box相匹配。标注为FP的红框内部没有任何目标物体,将其类别视为背景是一个负样本。
尽管一个Ground Truth可以与多个Default Box匹配,但是Ground Truth相对Default Box还是太少了,所以负样本相对正样本过多。为了保证正负样本尽量平衡,SSD采用了hard negative mining,即对负样本进行抽样,抽样时按照置信度误差(预测背景的置信度越小,误差越大)进行降序排列,选取误差的较大的top-k作为训练的负样本,以保证正负样本比例接近1:3。
5.3 损失函数
SSD的损失函数为: L ( x , c , l , g ) = 1 N ( L c o n f ( x , c ) + α L l o c ( x , l , g ) ) L(x,c,l,g)=\frac 1 N(L_{conf}(x,c)+αL_{loc}(x,l,g)) L(x,c,l,g)=N1(Lconf(x,c)+αLloc(x,l,g));损失由分类损失和定位损失的加权和构成,权重系数 α α α通常取 1 1 1。
5.3.1 定位损失
参照本文的编码解码方式,SSD的定位损失函数由定位结果(Default Box调整情况) l = ( l c x , l c y , l w , l h ) l=(l_{cx},l_{cy},l_{w},l_{h}) l=(lcx,lcy,lw,lh)与Ground Truth g = ( g c x , g c y , g w , g h ) g=(g_{cx},g_{cy},g_{w},g_{h}) g=(gcx,gcy,gw,gh)确定,Ground Truth编码值为 g ^ = ( g ^ c x , g ^ c y , g ^ w , g ^ h ) \hat{g}=({\hat{g}_{cx},\hat{g}_{cy},\hat{g}_{w},\hat{g}_{h}}) g^=(g^cx,g^cy,g^w,g^h)
L l o c ( x , l , g ) = ∑ i ∈ { P o s } N ∑ m ∈ c x , c y , w , h x i j k s m o o t h L 1 ( l i m − g ^ j m ) L_{loc}(x,l,g)=\sum_{i∈\{Pos\}}^{N}\sum_{m∈{cx,cy,w,h}}{x_{ij}^{k}smooth_{L1}(l_{i}^{m}-\hat{g}_{j}^{m})} Lloc(x,l,g)=i∈{Pos}∑Nm∈cx,cy,w,h∑xijksmoothL1(lim−g^jm)
g ^ j c x = ( g j c x − d i c x ) / d i w , g ^ j c y = ( g j c y − d i c y ) / d i h g ^ j w = l o g ( g j w d i w ) , g ^ j h = l o g ( g j h d i h ) \hat{g}_{j}^{cx}=(g_{j}^{cx}-d_{i}^{cx})/d_{i}^w,\hat{g}_{j}^{cy}=(g_{j}^{cy}-d_{i}^{cy})/d_{i}^h\\ \hat{g}_{j}^{w}=log(\frac {g_{j}^w} {d_{i}^w}),\hat{g}_{j}^{h}=log(\frac {g_{j}^h} {d_{i}^h}) g^jcx=(gjcx−dicx)/diw,g^jcy=(gjcy−dicy)/dihg^jw=log(diwgjw),g^jh=log(dihgjh)
其中 N N N为正样本数量, x i j k ∈ { 0 , 1 } x_{ij}^{k}∈\{0,1\} xijk∈{0,1}, x i j k = 1 x_{ij}^{k}=1 xijk=1表示第 i i i个Default Box与第 j j j个Ground Truth相匹配且ground truth内物体的类别为 k k k;SSD的损失函数在计算定位损失时只考虑了正样本的定位损失,负样本的定位损失不计算在内。
5.3.2 分类损失
SSD定义分类损失时对正负样本采取了不同的计算方式; c ^ i p \hat{c}_{i}^{p} c^ip表示第 i i i个正样本为类别 p p p的置信度, c ^ i 0 \hat{c}_{i}^{0} c^i0则代表类别为背景的负样本。简单来说,如果是正样本则使用交叉熵损失函数;如果是负样本则只对背景类进行优化不管其他类别。
结合编码方式、匹配策略、损失函数;损失计算的实现代码如下:
"""SSD MutiBoxLoss 损失计算. 摘自 MIT A Port Of SSD to Keras FrameWork"""
"""韩伟奇于2020年5月,代码中内容或注释若有问题欢迎批评指正 [email protected]"""
import tensorflow as tf
class MultiboxLoss(object):
"""Multibox loss with some helper functions.
# Arguments 参数说明
num_classes: Number of classes including background. 物体种类数量
alpha: Weight of L1-smooth loss. 权重系数,通常取1
neg_pos_ratio: Max ratio of negative to positive boxes in loss. 损失计算中负样本相对于正样本的最大比例(倍数)
background_label_id: Id of background label. 背景类标签,一般设置为0
negatives_for_hard: Number of negative boxes to consider
if there is no positive boxes in batch. batch中不存在正样本时,选取的负样本数量
# References
https://arxiv.org/abs/1512.02325 SSD论文地址
# TODO
Add possibility for background label id be not zero 未来加入对id非0的背景类的支持
"""
def __init__(self, num_classes, alpha=1.0, neg_pos_ratio=3.0,
background_label_id=0, negatives_for_hard=100.0):
self.num_classes = num_classes
self.alpha = alpha
self.neg_pos_ratio = neg_pos_ratio
if background_label_id != 0: #目前只支持背景类id为0的情况
raise Exception('Only 0 as background label id is supported')
self.background_label_id = background_label_id
self.negatives_for_hard = negatives_for_hard
def _l1_smooth_loss(self, y_true, y_pred):
"""Compute L1-smooth loss. 定位损失计算
# Arguments
y_true: Ground truth bounding boxes, Groud Truth 中的bounding box实际位置的编码值(Prior Box实际调整情况)
tensor of shape (?, num_boxes, 4). tensor 形状为(?, num_boxes, 4) ?代表batch_size num_boxes为"有效特征层"中Default Box的数量 4表示Default Box调整情况
y_pred: Predicted bounding boxes, 网络预测的bounding box(Prior Box预测调整情况)
tensor of shape (?, num_boxes, 4). tensor 形状为(?, num_boxes, 4)
# Returns
l1_loss: L1-smooth loss, tensor of shape (?, num_boxes). 返回值为每个Default Box的定位计算损失
# References
https://arxiv.org/abs/1504.08083
"""
abs_loss = tf.abs(y_true - y_pred)
sq_loss = 0.5 * (y_true - y_pred)**2
l1_loss = tf.where(tf.less(abs_loss, 1.0), sq_loss, abs_loss - 0.5)
return tf.reduce_sum(l1_loss, -1)
def _softmax_loss(self, y_true, y_pred):
"""Compute softmax loss. 分类损失计算
# Arguments
y_true: Ground truth targets, Ground Truth中实际bounding box类别的编码(每个Prior Box对应的类别)
tensor of shape (?, num_boxes, num_classes). tensor 形状为(?, num_boxes, num_classes) num_classes为类别总数(包含背景)
y_pred: Predicted logits,
tensor of shape (?, num_boxes, num_classes).
# Returns
softmax_loss: Softmax loss, tensor of shape (?, num_boxes). 返回值为每个Prior Box的分类损失
"""
y_pred = tf.maximum(tf.minimum(y_pred, 1 - 1e-15), 1e-15)
softmax_loss = -tf.reduce_sum(y_true * tf.log(y_pred),
axis=-1)
return softmax_loss
def compute_loss(self, y_true, y_pred):
"""Compute mutlibox loss. SSD总损失计算
# Arguments
y_true: Ground truth targets, y_true为Ground Truth的编码结果
tensor of shape (?, num_boxes, 4 + num_classes + 8), ?:batch_size 4:Prior Box调整情况,num_classes:每个类别的置信度
priors in ground truth are fictitious, 8:
y_true[:, :, -8] has 1 if prior should be penalized y_true[:, :, -8]=1 表示该框为需要调整参数来预测Ground Truth的正样本
or in other words is assigned to some ground truth box,
y_true[:, :, -7:] are all 0.
y_pred: Predicted logits,
tensor of shape (?, num_boxes, 4 + num_classes + 8).
# Returns
loss: Loss for prediction, tensor of shape (?,).
"""
batch_size = tf.shape(y_true)[0]
num_boxes = tf.to_float(tf.shape(y_true)[1]) #获取Default Box数量
# loss for all priors 计算所有样本损失
conf_loss = self._softmax_loss(y_true[:, :, 4:-8],
y_pred[:, :, 4:-8]) #所有分类损失 shape:(batch_size,8732,num_classes) -> (batch_size,8732)
loc_loss = self._l1_smooth_loss(y_true[:, :, :4],
y_pred[:, :, :4]) #所有定位损失 shape:(batch_size,8732,4) -> (batch_size,8732)
# get positives loss 获取正样本损失
num_pos = tf.reduce_sum(y_true[:, :, -8], axis=-1) #计算每一张图片正样本数量,y_true[:, :, -8]=1表示该样本为正样本,shpe:(batch_size)
pos_loc_loss = tf.reduce_sum(loc_loss * y_true[:, :, -8],
axis=1) #计算每一张图片正样本的定位损失,shape:(batch_size)
pos_conf_loss = tf.reduce_sum(conf_loss * y_true[:, :, -8],
axis=1) #计算每一张图片正样本的分类损失,shape:(batch_size)
# get negatives loss, we penalize only confidence here 计算负样本损失,只计算置信度损失不考虑定位损失
num_neg = tf.minimum(self.neg_pos_ratio * num_pos,
num_boxes - num_pos) #计算每张图片中负样本数量: (预先设定的比例*正样本数量)与(所有prior box去掉正样本后的数量)中的最小值
pos_num_neg_mask = tf.greater(num_neg, 0) #获取一个01标记张量,1表示该图片中有负样本,0表示没有 shape:(batch_size)
has_min = tf.to_float(tf.reduce_any(pos_num_neg_mask))
num_neg = tf.concat(axis=0, values=[num_neg,
[(1 - has_min) * self.negatives_for_hard]])
num_neg_batch = tf.reduce_min(tf.boolean_mask(num_neg,
tf.greater(num_neg, 0)))
num_neg_batch = tf.to_int32(num_neg_batch)
confs_start = 4 + self.background_label_id + 1 #计算除背景类外其余类别置信度的起始索引
confs_end = confs_start + self.num_classes - 1 #计算除背景类外其余类别置信度的终止索引
max_confs = tf.reduce_max(y_pred[:, :, confs_start:confs_end],
axis=2) #选出每个Prior Box中置信度最高的类别作为该Prior Box的物体种类
_, indices = tf.nn.top_k(max_confs * (1 - y_true[:, :, -8]), #筛选出类别应该为背景类的Prior Box作为备选负样本
k=num_neg_batch) #选取备选负样本中置信度最高top_k个作为负样本(原本该Prior Box应该预测到背景却预测到其他物体;其置信度还比较高)
batch_idx = tf.expand_dims(tf.range(0, batch_size), 1)
batch_idx = tf.tile(batch_idx, (1, num_neg_batch)) #找到负样本在1维上的索引
full_indices = (tf.reshape(batch_idx, [-1]) * tf.to_int32(num_boxes) +
tf.reshape(indices, [-1]))
# full_indices = tf.concat(2, [tf.expand_dims(batch_idx, 2),
# tf.expand_dims(indices, 2)])
# neg_conf_loss = tf.gather_nd(conf_loss, full_indices)
neg_conf_loss = tf.gather(tf.reshape(conf_loss, [-1]),
full_indices)
neg_conf_loss = tf.reshape(neg_conf_loss,
[batch_size, num_neg_batch])
neg_conf_loss = tf.reduce_sum(neg_conf_loss, axis=1)
# loss is sum of positives and negatives
total_loss = pos_conf_loss + neg_conf_loss
total_loss /= (num_pos + tf.to_float(num_neg_batch))
num_pos = tf.where(tf.not_equal(num_pos, 0), num_pos,
tf.ones_like(num_pos))
total_loss += (self.alpha * pos_loc_loss) / num_pos
return total_loss