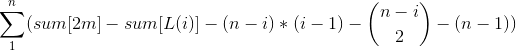HDU--4609（FFT，计数）

2015-07-28 01:56:55

【传送门】

题意：很短，给出最多10^5个数 L[1] ~ L[n]（数的范围：[1,10^5]），问任意挑选3个数以其为边长能组成三角形的概率。

思路：首先考虑三角形的判定：任意两边和大于第三边。对于10^5个数，两两求和显然不够快，但是我们可以这样：统计每个数的出现次数，然后把每个数看成m阶多项式的系数（m由数的最大值决定），就像：a0 + a1*x + a2*x^2 + ... + ak*x^k + ... 这样的形式，然后让多项式和自己进行卷积，得到一个2m阶的多项式，x^k 的系数 ak 其实就代表了在原来的数列中任意选两个数相加得到 k 的方案数（选的两个数可重）。因为有重复选同一个数的情况，我们可以用 O(n) 的循环来消除这种影响。

　　然后我们将原来的数列升序排序，再枚举 L[i] 为最长边累加方案数。当 L[i] 为最长边时，首先要知道两数之和比 L[i] 大的方案数，其实就是 Sigma(a(L[i]+1) ... a[2m] )，这个可以通过计算前缀和 sum[] 来 O(1) 实现。但是这其中有些方案中 L[i] 不是最长边，或者 L[i] 在之前就已经被选掉了，那么就要去掉这些情况：（1）两边都比 L[i] 大，为 C(n - i , 2)  ； （2）一条边比 L[i] 大，另一条小于 L[i]，为 (n - i) * (i - 1) ；（3）L[i] 已经被选，为 1 * (n - 1) 。

　　最后的公式形式：

 

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

typedef long long ll;
const int MAXN = (1 << 18) + 10;
const double DPI = 2.0 * acos(-1.0);

int T,n,N,bit,tmax,tmax2;
int L[MAXN],rev[MAXN];
ll sum[MAXN];

struct CP{
    double a,b;
    CP(double ta = 0,double tb = 0) : a(ta) , b(tb) {}
}A1[MAXN],A2[MAXN];

inline CP operator * (CP &a,CP &b){return CP(a.a*b.a-a.b*b.b,a.a*b.b+a.b*b.a);}
inline CP operator + (CP &a,CP &b){return CP(a.a + b.a,a.b + b.b);}
inline CP operator - (CP &a,CP &b){return CP(a.a - b.a,a.b - b.b);}

void Pre(){
    for(N = 1,bit = 0; N < tmax2; N <<= 1,bit++);
    for(int i = 1; i < N; ++i)
        rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
}

void FFT(CP *A,int n,int f){
    for(int i = 0; i < n; ++i) if(i < rev[i]) swap(A[i],A[rev[i]]);
    for(int m = 2; m <= n; m <<= 1){
        CP wm(cos(DPI / m),f * sin(DPI / m));
        for(int k = 0; k < n; k += m){
            CP w(1,0);
            for(int j = 0; j < (m >> 1); ++j){
                CP t = w * A[k + j + (m >> 1)];
                CP u = A[k + j];
                A[k + j] = u + t;
                A[k + j + (m >> 1)] = u - t;
                w = w * wm;
            }
        }
    }
    if(f == -1) for(int i = 0; i < n; ++i) A[i].a /= n;
}

void Solve(){
    for(int i = 0; i < N; ++i) A1[i] = CP(0,0),A2[i] = CP(0,0);
    for(int i = 1; i <= n; ++i){
        A1[L[i]].a += 1;
        A2[L[i]].a += 1;
    }
    FFT(A1,N,1); FFT(A2,N,1);
    for(int i = 0; i < N; ++i) A1[i] = A1[i] * A2[i];
    FFT(A1,N,-1);
    sum[0] = 0;
    sort(L + 1,L + n + 1);
    for(int i = 1; i <= n; ++i) A1[L[i] << 1].a -= 1;
    for(int i = 0; i < tmax2; ++i) sum[i] = sum[i - 1] + (ll)(A1[i].a + 0.5)/2;
    ll ans = 0;
    for(int i = 1; i <= n; ++i){ //枚举最长边
        ans += sum[tmax2 - 1] - sum[L[i]];
        ans -= (ll)(n - i) * (i - 1) + (ll)(n - i) * (n - i - 1) / 2 + n - 1;
    }
    printf("%.7f\n",1.0 * ans / ((ll)n * (n - 1) * (n - 2) / 6));
}

inline int Read(){
    int x = 0; char ch = getchar();
    while(ch < '0' || ch > '9') ch = getchar();
    while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}
    return x;
}

int main(){
    T = Read();
    while(T--){
        tmax = 0;
        n = Read();
        for(int i = 1; i <= n; ++i){
            L[i] = Read();
            tmax = max(tmax,L[i]);
        }
        tmax++;
        tmax2 = tmax + tmax - 1;
        Pre();
        Solve();
    }
    return 0;
}

 

转载于:https://www.cnblogs.com/naturepengchen/articles/4681711.html