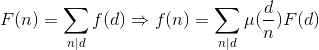HDU1695+HDU6390 莫比乌斯反演入门+分块思想。

HDU1695

莫比乌斯反演两个公式

思路：该题的题意是给你两个范围，1~n，1~m，求x属于1~n，y属于1~m， 且GCD（x，y）==k，这样的有多少对。

等同于求1~n/k, 1~m/k, gcd(x,y)==1,的对数。令f（t）为gcd（x， y）等于t的个数，F（n）等于gcd（x， y）=t的倍数的个数。

所以可以用第二个公式，就是说gcd（x,y）等于t的倍数的所有个数=每个gcd（x，y）等于T（t|T）的个数的和。有点绕，就是整体和局部的关系。

根据公式可以反演出第二个式子。好处就是，现在我们要求gcd（x， y）==1的个数，我们不好直接求出来，但是我们可以求出F（T）（t|T），F（T）=(n/T)*(m/T)。带入反演出来的第二个公式就解决了。时间复杂度为O(T*n)

#include
using namespace std;
typedef long long ll;
const int N=100010;
bool check[N];
int prime[N];
int mu[N];
void Moblus(){//O（n）求mu[]
    memset(check, false, sizeof check);
    mu[1]=1;
    int tot=0;
    for(int i=2; i=N) break;
            check[i*prime[j]]=true;
            if(i%prime[j]==0){
                mu[i*prime[j]]=0;
                break;
            }
            else{
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
}

int main(){
    Moblus();
    int T, a, b, c, d, k, cas=0;
    scanf("%d", &T);
    while(T--){
        scanf("%d%d%d%d%d", &a, &b, &c, &d, &k);

        if(k==0){
            printf("Case %d: 0\n", ++cas);
            continue;
        }
        int n=b/k, m=d/k;
        int mn=min(n, m);
        ll ans1=0, ans2=0;
        for(int i=1; i<=mn; i++){
            ans1+=1ll*mu[i]*(n/i)*(m/i);
        }
        for(int i=1; i<=mn; i++){
            ans2+=1ll*mu[i]*(mn/i)*(mn/i);
        }
        //printf("%lld %lld\n", ans1, ans2);
        printf("Case %d: %lld\n", ++cas, ans1-ans2/2);
    }
    return 0;
}

/****分块写，时间节省一半***/
#include
using namespace std;
typedef long long ll;
const int N=1e5+10;
int prime[N], mu[N], sum[N];
bool check[N];
void Moblus(){//O（n）求mu[]
    memset(check, false, sizeof check);
    mu[1]=1;
    int tot=0;
    for(int i=2; i=N) break;
            check[i*prime[j]]=true;
            if(i%prime[j]==0){
                mu[i*prime[j]]=0;
                break;
            }
            else{
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
    for(int i=1; i

HDU6390

该题和上题是一样的。只不过需要一部转化。

ϕ(ab)/ϕ(a)ϕ(b)=gcd(a,b)/φ(gcd(a,b))；（我也不懂什么原理）

所以我们只需要枚举gcd，然后跟上题思路一样求和就行。复杂度O（n*log（n））

#include
using namespace std;
typedef long long ll;
const int N=1e6+10;
ll prime[N], mu[N], mo, inv[N], phi[N];
ll gcd[N];
bool check[N];

void Moblus(){
    memset(check, false, sizeof check);
    mu[1]=1;
    int tot=0;
    for(int i=2; i<=1e6; i++){
        if(!check[i]){
            prime[tot++]=i;
            mu[i]=-1;
        }
        for(int j=0; j1e6) break;
            check[i*prime[j]]=true;
            if(i%prime[j]==0){
                mu[i*prime[j]]=0;
                break;
            }
            else{
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
}

void phi_table(){//O（nloglogn）
    for(int i=2; i<=1e6; i++) phi[i]=0;
    phi[1]=1;
    for(int i=2; i<=1e6; i++) if(!phi[i])
    for(int j=i; j<=1e6; j+=i){
        if(!phi[j]) phi[j]=j;
        phi[j]=phi[j]/i*(i-1);
    }
}

void getInv(int up){
    inv[1]=1;
    for(int i=2; i<=up; i++)
        inv[i]=inv[mo%i]*(mo-(mo/i))%mo;
}

ll get(int n,int m)
{
    ll ans=0;
    int up=min(n, m);
    for(int i=1;i<=up;i++)
        ans=(ans+mu[i]*(n/i)*(m/i))%mo;
    return ans;
}


int main(){
    phi_table();
    Moblus();
    int T, n, m;
    scanf("%d", &T);
    while(T--){
        scanf("%d%d%lld", &n, &m, &mo);
        int k=min(n, m);
        getInv(k);
        for(int i=1; i<=k; i++)
            gcd[i]=1ll*i*inv[phi[i]]%mo;
        ll ans=0;
        for(int i=1; i<=k; i++){
            int tn=n/i, tm=m/i;

            ans=(ans+gcd[i]*get(tn, tm))%mo;//这里很疑惑，我直接在这写循环求就T，写成函数就不T了，很不解。
        }
        printf("%lld\n", ans);
    }
    return 0;
}

对于上面在循环里面不用函数求超时的情况，我们可以用分块的思想将其优化，可以将时间优化到上面的一半，上面跑了1000ms，这个跑了400ms。分块的思想就是对于n/j，m/j这两个数，j在变的时候这个比值的下取整不一定变。利用这个特性可以提出这一部分然后求mu[]的前缀和，这样会大大节省时间。

#include
using namespace std;
typedef long long ll;
const int N=1e6+10;
int prime[N], mu[N], sum[N], mo, phi[N], inv[N];
bool check[N];
void Moblus(){//O（n）求mu[]
    memset(check, false, sizeof check);
    mu[1]=1;
    int tot=0;
    for(int i=2; i=N) break;
            check[i*prime[j]]=true;
            if(i%prime[j]==0){
                mu[i*prime[j]]=0;
                break;
            }
            else{
                mu[i*prime[j]]=-mu[i];
            }
        }
    }
    for(int i=1; i