数据结构7——主席树初步
![]()
本作品采用知识共享署名-相同方式共享 4.0 国际许可协议进行许可。
好吧为什么我突然想起来要去写主席树呢?因为在做codeforces 787E这题的时候,我用了二分+剪枝的算法莫名其妙的过了,然而时间复杂度算出来感觉不对。网上一查,也有这么过的,但是主要还是写了主席树,所以回来想到是不是应该学一下主席树。
主席树最经典的应用就是在求区间第 k k k大的问题了。我们来看一下例题POJ 2104。题目大意就是求区间第 k k k大,数据范围 n ≤ 1 0 5 , m ≤ 5 × 1 0 3 n\le 10^5, m\le 5\times 10^3 n≤105,m≤5×103。
题目描述
You are working for Macrohard company in data structures department. After failing your previous task about key insertion you were asked to write a new data structure that would be able to return quickly k-th order statistics in the array segment.
That is, given an array a [ 1... n ] a[1...n] a[1...n] of different integer numbers, your program must answer a series of questions Q ( i , j , k ) Q(i, j, k) Q(i,j,k) in the form: “What would be the k-th number in a [ i . . . j ] a[i...j] a[i...j] segment, if this segment was sorted?”
For example, consider the array a = ( 1 , 5 , 2 , 6 , 3 , 7 , 4 ) a = (1, 5, 2, 6, 3, 7, 4) a=(1,5,2,6,3,7,4). Let the question be Q ( 2 , 5 , 3 ) Q(2, 5, 3) Q(2,5,3). The segment a [ 2...5 ] a[2...5] a[2...5] is ( 5 , 2 , 6 , 3 ) (5, 2, 6, 3) (5,2,6,3). If we sort this segment, we get ( 2 , 3 , 5 , 6 ) (2, 3, 5, 6) (2,3,5,6), the third number is 5 5 5, and therefore the answer to the question is 5 5 5.
样例
| Input | Ouput |
|---|---|
| 7 31 5 2 6 3 7 42 5 34 4 11 7 3 | 563 |
解题思路
我们首先考虑如何暴力地维护这个东西。
我们知道,对于一个给定的数列 a [ 1... n ] a[1...n] a[1...n]的第 k k k大,我们可以将其离散化,也就是每个数对应的编号是它在数列里从大到小排的第 i i i个。然后建立一个线段树来维护这个离散后的区间 o r d [ 1... n ] ord[1...n] ord[1...n]。
简单来说,比如数列 { 1 , 1 , 4 , 5 , 1 , 4 } \{1,1,4,5,1,4\} {1,1,4,5,1,4},我们注意到 1 1 1出现 3 3 3次, 4 4 4出现 2 2 2次, 5 5 5出现 1 1 1次,那么我们离散化之后, 1 1 1就对应编号 1 1 1, 4 4 4对应编号 2 2 2, 5 5 5对应编号 3 3 3,其中编号为 1 1 1的出现了 3 3 3次(以此类推),得到数组 b = { 3 , 2 , 1 } b=\{3,2,1\} b={3,2,1}。数组 b b b就表示出现的次数。然后建一个线段树维护数组 b b b。这个操作实际上是每次对于一个叶节点,将该叶节点到根路径上的点全部权值加 1 1 1。
接下来怎么查找第 k k k大呢?我们可以在整颗线段树上二分,对应当前节点 o o o,如果 o o o控制的区间里出现的次数大于当前查的 r a n k rank rank,那么我们就在 o o o的左儿子里继续二分,查找第 r a n k rank rank大的位置;否则在右儿子里二分,查第 r a n k − s z rank-sz rank−sz大的位置,其中 s z sz sz表示 o o o左儿子控制的大小。这个递归原理比较简单,这里不再多说。
但是这个算法对于给定区间 [ 1 , x ] [1,x] [1,x]查询的复杂度是 O ( n log 2 n ) O(n \log_2 n) O(nlog2n)。对于任意区间,我们需要维护 n n n棵线段树,第 i i i棵维护 [ 1 , i ] [1,i] [1,i]的区间第 k k k大,这样当查 [ l , r ] [l,r] [l,r]时,我们就可以用 [ 1 , r ] − [ 1 , l ) [1,r]-[1,l) [1,r]−[1,l)来求答案了。复杂度变成 O ( n 2 ⋅ log 2 n + q ⋅ log n ) O(n^2 \cdot \log_2 n + q\cdot \log n) O(n2⋅log2n+q⋅logn)。太大了。
于是我们考虑优化一下这个线段树。
我们知道,我们在维护第 i i i个线段树的时候,对于第 i + 1 i+1 i+1个线段树,我们只修改了其中的一条链——就是 a [ i + 1 ] a[i+1] a[i+1]对应的那条,那么我们是不是可以不用特意建一棵树呢?于是我们找到了一个办法——只把路径上的那一串点全部用新的点替代,剩下的不变!于是就变成了下面这样的图。注意,每次修改完之后,我们要把 o r d ord ord数组对应的点(就是离散化的编号)换成新的。
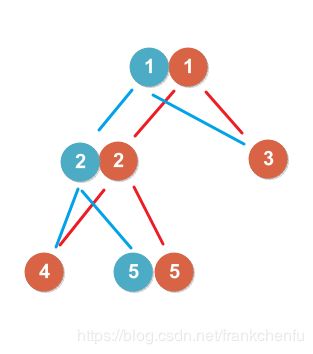
每一次的操作都是 O ( log 2 n ) O(\log_2 n) O(log2n)的,空间每次也只增加了 O ( log 2 n ) O(\log_2 n) O(log2n)。于是我们 n n n棵线段树总的维护时间就是 O ( n log 2 n ) O(n\log_2 n) O(nlog2n),空间 O ( n log 2 n ) O(n\log_2 n) O(nlog2n),查询是 O ( q log 2 n ) O(q\log_2 n) O(qlog2n)的。我们就很愉快的解决了这个问题。
代码
#include总结
主席树一般可以用来求解区间第 k k k大问题,是线段树的一种拓展,融合了树上二分、等效替代等多种思想。
对于主席树其实还有一个名称叫可持久化线段树,他们之间有什么联系呢?
可持久化,就是要查询历史版本。想一下我们每次更新的时候是怎么做的吗?加入新点,扔掉旧点——我想你应该明白了,如果把这些旧点回收利用,那么我们就可以知道它以前长什么样。
还是感觉有点复杂的。