关系规范化之函数依赖集闭包和属性集X对于函数依赖集F的闭包
最近在学数据库原理,关系规范化中介绍了几个算法,最基础也最重要的就是求属性集X关于某个函数依赖集合F的闭包。
/*8周的功夫一本数据库基本原理就学完了,很快要考试了,所以5-1假期也没打算出去玩,就在学校了复习、休息等等。就在复习的过程中,突然发现书上对于函数依赖集合的闭包,以及属性集合的闭包的区别,几乎没有介绍。我看了好几遍才看懂,所以特此补充,以便同我有相同疑问的朋友理解。*/
/*这是在2016年五一劳动节修改的,哈哈,我是中国好程序员,劳动节就劳动得度过[]~( ̄▽ ̄)~*。之前求闭包没有采用递归的方式,过程十分繁琐,不值得推荐,所以删去的之前的那段代码。采用递归,更加贴近定义,思路更加清晰。此外,精简优化了一下代码,删除了一些不必要的函数,或者转换更好的思路,代码量得到了精简。*/
首先说一下,函数依赖集的闭包
----------------------------------------------------分割线-------------------------------------------------------------------------------------------
函数依赖的闭包
定义:若F为关系模式R(U)的函数依赖集,我们把F以及所有被F逻辑蕴涵的函数依赖的集合称为F的闭包,记为F+。
什么是“被F逻辑蕴涵"呢?
函数依赖的逻辑蕴涵:
定义:设有关系模式R(U)及其函数依赖集F,如果对于R的任一个满足F的关系r函数依赖X→Y都成立,则称F逻辑蕴涵X→Y,或称X→Y可以由F推出。
例:关系模式 R=(A,B,C),函数依赖集F={A→B,B→C}, F逻辑蕴涵A→C
所以说:函数依赖集F的闭包,里面的元素还是函数依赖(就是X→Y这种东西),函数依赖集F的闭包包括F自身,加上能从F中通过Armstong公理推导出的,新的函数依赖。
即:F+={X→Y|X→Y∈F∨“应用Armstong公理从F中导出的任何X→Y”}
为了判断函数依赖X->Y是否在F+中,只要计算出F+即可。因为F+是由F根据Armstrong公理导出的函数依赖的集合。因此,原则上说,只要按照Armstrong公理系统中的推理规则就可以计算出F+。但是,闭包F+的计算是一件很麻烦的事情,因为计算F+的问题是一个NP完全问题,即若F={X->A1, X->A2, …, X->An,},则需要计算F+的O(2n)个函数依赖,因此,当 n比较大时,实际计算F+是不可行的。即使F的元素不多时, F+中的元素也可能很多。此外,闭包F+中也存在许多冗余信息。其实,判断一个函数依赖X->Y是否在F+中,完全不必计算闭包F+
一个重要的定理:X->Y属于F+,等价于Y属于X关于F的闭包。X,Y都是F中的属性。
那什么是属性X关于F的闭包呢?
----------------------------------------------------分割线-------------------------------------------------------------------------------------------
2.属性集X(X∈U)对于U上的一个函数依赖集F的闭包X_F^+
(1)定义: 设关系模式R(U,F ),U 为其属性集,F 为其函数依赖集,则称在所有用Armstrong 公理从F 推出的函数依赖X → Ai 中,Ai 的属性集合为X 的属性闭包。
也就是说,属性集X关于函数依赖集合的闭包,里面的元素是属性(而不是函数依赖),这些属性是F根据Armstrong 公理推导出来的。
好吧为了充分理解,补充一下什么是Armstrong 公理:
Armstrong公理
1、定理:若U为关系模式R的属性全集,F为U上的一组函数依赖,设X、Y、Z、W均为R的子集,对R(U,F)有:
F1(自反性):若X≥Y(表X包含Y),则X→Y为F所蕴涵;(F1':X→X)
F2(增广性): 若X→Y为F所蕴涵,则XZ→YZ为F所蕴涵;(F2':XZ→Y)
F3(传递性): 若X→Y,Y→Z为F所蕴涵,则X→Z为F所蕴涵;
F4(伪增性):若X→Y,W≥Z(表W包含Z)为F所蕴涵,则XW→YZ为F所蕴涵;
F5(伪传性): 若X→Y,YW→Z为F所蕴涵, 则XW→Z为F所蕴涵;
F6(合成性): 若X→Y,X→Z为F所蕴涵,则X→YZ为F所蕴涵;
F7(分解性): 若X→Y,Z≤Y (表Z包含于Y)为F所蕴涵,则X→Z为F所蕴涵。
函数依赖推理规则F1∽F7都是正确的。
2、Armstrong公理:
推理规则F1、F2、F3合称Armstrong公理;
F4 ∽ F7可由F1、F2、F3推得,是Armstrong公理的推论部分。
(2)计算: 求属性集X 关于函数依赖F 的属性闭包X+。设关系模式R 的全部属性集为U,在U 上的函数依赖集为F,U 的一个子集为X,计算X 关于F 的属性闭包X+ 。
具体方法如下:
①置初始X(0)= Ф,X(1)=X;
②如果X(0)≠ X(1),置X(0)=X(1),否则转④;
③对F 中的每一个函数依赖Y → Z,若Y X(1),置X(1)=X(1)∪ Z,转②;
④结束,即X(1)为X+。
下面我们借助一个例子来说明属性闭包的计算过程。
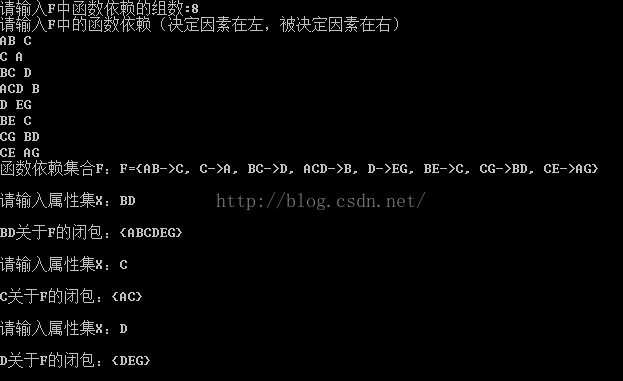
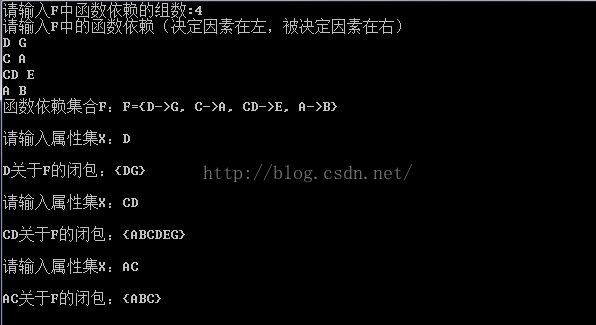
例1: 设有关系模式R(U,F),其中U={A,B,C,D,E},F={ AB → C,B → D,C → E,CE → B,AC → B},计算(AB)+。
解: 由上述算法得:
第一次: ① X(0)= Ф,X(1)=AB;
②由于X(0)≠ AB,置X(0)=AB;
③搜索F中的每一个函数依赖,得AB →C与B→D为AB,B X(1),置X(1)=AB ∪ C ∪ D=ABCD;
第二次: ② X(0)≠ ABCD,则X(0)=ABCD;
③找到C → E 与AC → B,置X(1)=ABCD ∪ E ∪ B=ABCDE;
第三次: ② X(0)≠ ABCDE,则X(0)=ABCDE;
③找到CE → B,置X(1)=ABCDE ∪ B=ABCDE;
第四次: ② X(0)=X(1),转④;
④结束,即X(1)=(AB)+=ABCDE。
为了简便,将各个属性用字符表示,程序如下:
//求属性集X(X∈U)对于U上的一个函数依赖集F的闭包X_F^+
//输入:属性全集U,U上的函数依赖F,属性集X (X∈U)
//输出:X关于F的闭包 X_F^+
#include
#include
using namespace std;
struct FunctionDependence//函数依赖
{
string X;//决定因素
string Y;
};
void Init (FunctionDependence FD[],int n)
{
//函数依赖关系初始化
int i;
string x,y;
cout<<"请输入F中的函数依赖(决定因素在左,被决定因素在右)"<>x>>y;
FD[i].X=x;
FD[i].Y=y;
}
cout<<"函数依赖集合F:";
cout<<"F={" ;
for (i=0;i"<=1)//cout<<(char)ii;
closure+=(char)ii;
}
return closure;
}
string X_Fn(FunctionDependence FD[],int n,string &xx)
{
string yy=xx;
for (int i=0;i> xx;
cout<<"\n"<>N;
FunctionDependence fd[N];
Init(fd,N);
FD(fd,N);
FD(fd,N);
FD(fd,N);
return 0;
}