jea_dong

为什么数据结构总是成为程序员的噩梦？

前言

结构和关系

结构的变化

数据结构

查找

排序

总结

知识点总结

前言

每次自己回想起大学上《数据结构》课程的时候，都感觉像是一场噩梦。脑海中浮现的都是复杂的数学公式、看不懂的C语言算法、抽象的递归等等。大学为了学分也只能硬着头皮完成了考试，然后就没有然后了，完全没记住学了些什么。工作以后，增删改查的业务模块中几乎没有看到数据结构中那些复杂的算法。于是慢慢的就忘记了还有数据结构这样噩梦般的知识。

难道《数据结构》就是大学老师为了折磨我们而必修的一门课程吗？

答案肯定是否定的。其实开发工作中大量的使用了数据结构的知识，只是这些复杂的算法和实现过程都被开发工具给我们封装好了。比如数据库的查询和索引，JDK的容器API，JVM中的堆和栈、MQ的消息队列等等。

那么我们还有必要学习数据结构知识吗？

答案是肯定的。

1、数据结构的逻辑模型能让我们设计的系统架构更加合理；

2、数据结构的逻辑模型能让我们业务模型更加简单；

3、数据结构的物理模型能让我们利用内存空间更加高效；

4、数据结构的算法能提升程序的执行效率，节省CPU消耗，提升用户体验，支持更多并发请求等等；

数据结构有这么多好处，是编程能力的核心技能。那么就让我们来好好的重新认识它。大家对数据结构的恐惧主要是算法的细节和实现，所以咱们先屏蔽算法实现，只讨论逻辑概念和它能解决什么问题。

结构和关系

在研究数据结构之前，咱们先要补充结构相关的概念。什么是结构呢？科学的定义太抽象咱们就不讨论了。日常生活中接触到的结构有建筑结构、化学结构、汽车结构、知识结构等。化学结构是指元素之间的关系。汽车结构是指组件之间的关系。那么我们可以简单的理解结构就是元素之间的关系。“元素”在不同的领域指代的事物不一样。我们看到的这些结构都非常复杂，组件元素很复杂，元素之间关系也很复杂。那么我们怎么去研究呢？复杂的元素都是由最简单的基本元素组成的；复杂的关系都是由最简单的基本关系组成的。所以我们应该从这些基础元素和基础关系入手。由于元素是变化的，因此我们主要研究结构的关系而不是元素。

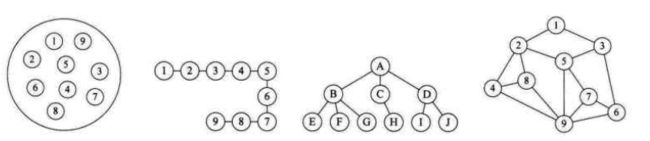
通过人们的研究，总结出了四种结构的逻辑关系。

1、集合结构，表示元素之间的平等关系；

2、线性结构，表示元素之间的一对一关系；

3、树形结构，表示元素之间的一对多关系；

4、图形结构，表示元素之间的多对多关系。

这些结构都是怎么总结出来的呢？咱们还是先找找对应的结构案例来看看。

集合结构，相当于人类最原始的部落，大家住在同一个村落中。如果跟其他部落打架，大家就一起上，看谁更勇敢。

线性结构，后来大家商量不要群殴了，咱们就各派3个人出来玩KOF，一对一单挑。3个人出场顺序就是线性结构。如果是排前面的先出场，就是队列结构，先进先出。如果是排后面的先出场，就是栈结构，先进后出。咱们中国历史上经典的“田忌赛马”，就是这个原理。

树形结构，再后来部落人数越来越多了，打架就不好操作了。于是人们想出了军队的概念，5个人一个班，3个班一个排，3个排一个连，后面还有营、团、旅、师、军，大家感兴趣可以去百度一下。这样的军队结构就是一个树形结构，表示一对多的关系。

图形结构，有了军队以后，大家打架就不是简单的互殴了，要根据地形讲究战略战术。那么怎么表示各个部落之间的位置和路线呢？一个部落到其他部落是有多条路线的，这些信息组成了地图。这种网状结构就是图形结构，表示多对多的关系。

结构的变化

现在我们已经搞清楚了结构和关系，但是结构并不是始终不变的。它是会根据元素的变化做出相应的变化。我们下面就来看看结构都有哪些变化？总的来说结构变化有3种情况，增加元素、删除元素、修改元素。

咱们前面了解的四种逻辑结构对三种变化进行的操作是不一样的。修改只是元素自身变化，不影响结构，咱们就只研究增加和删除。集合结构，由于元素是平等关系，增加和删除元素对结构没有影响，只要集合的空间足够就行。线性结构，树形结构和图形结构中任何元素的增加和删除都会对结构造成影响。由于咱们这里篇幅有限，就不展开讨论增加和删除操作对4种结构的影响了。

数据结构

前面铺垫了这么久，就是为了让大家先对数据结构的重要性和基本概念有个感性认识。总结起来内容不多，我们知道了四种逻辑结构和三种元素变化。那么接下来我们就要看看在计算机的世界里面，该如何表示这些逻辑结构和元素变化呢？我们需要补充一下数据结构的计算机概念。

数据结构中的元素叫做数据元素。数据元素有多个数据子项。例如数据库的记录和字段。

我们把逻辑结构在计算机的表示方式叫做物理结构。有两种物理结构：顺序存储结构、链式存储结构。

顺序存储结构，连续的内存空间来保存元素。例如数组。

链式存储结构，元素之间物理位置不连续，每个元素需要额外存储下一个元素的物理地址。例如链表。

数据结构要研究的内容就是怎么用这两种物理结构来表示四种逻辑结构，并且要实现元素变化的结构操作。这些知识非常的复杂和枯燥，大家可以先跳过，只关心JDK已经封装好的API就好。然后在掌握了API的使用方法之后，再慢慢的去看底层实现原理。这样有的放矢的学习要轻松很多，而且还可以边做实验变理解。

我们还是把树形结构和图形结构的存储结构讲解一下。树形结构是一对多的关系，所以每个点都有子节点列表。第一个节点叫做根节点。一棵树就是从根节点开始，每个子节点又有自己的子节点，这样一直递归下去。递归的概念很抽象，我们这里只是简单理解为重复自己的结构或者逻辑。比如愚公移山中所说，父亲有儿子，儿子还有儿子，子子孙孙无穷尽也。图形结构有两种元素，节点和路径。图的物理结构也有两种方式，矩阵法和链表法。图的结构复杂并且应用场景非常特殊，咱们暂时先不展开讨论。

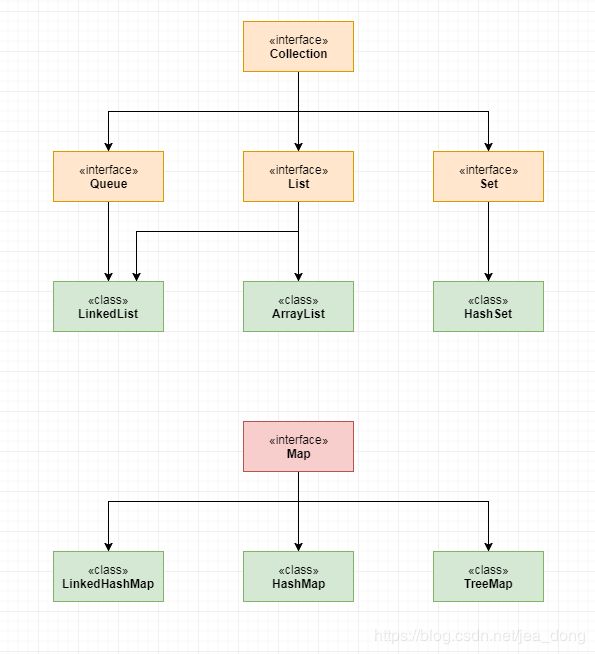
这里做个提醒，数据结构中的集合和图跟JDK中的Collect和Map是两回事。大家在学习的时候要注意一下，别弄混了。

我把它们的对应关系做了梳理，大家可以参考一下。

集合结构：Set、Map、HashMap、TreeMap

线性结构：数组、List、ArrayList、LinkedList（队列和栈）

树形结构和图形结构：需要自己实现。

集合工具：Collections、Arrays

查找

数据结构的实现不是我们需要关心的重点，相信大家在学习开发语言的时候就掌握得很好了。我们主要关心的内容是数据结构的遍历、排序和查找算法。我们还是老规矩需要补充新的概念，算法。

算法是解决问题的求解步骤。或者叫解决问题的方法。

算法有五个特性：输入、输出、有穷性、确定性、可行性。

算法有五个要求：正确性、可读性、健壮性、执行效率高、使用空间少。

解释一下算法的五个特性和五个要求，特性是定义什么是算法，要求是定义什么是好算法。

算法特性很好理解，就是编程语言中的方法。这里的输入和输出指逻辑上的概念，不是语法上方法的参数和返回值，我觉得可以理解成数据和结果。有穷性就是说不能有死循环。确定性和可行性是说每条指令都是计算机可以执行的，不是程序伪码。

算法要求更加实在一些，就是咱们的代码规范。正确性和健壮性要求不能有BUG。可读性要求人能轻松看懂代码逻辑。效率和空间就是要求算法要精妙，衍生出了一个新概念叫算法复杂度。算法复杂度有时间和空间两个维度，我们一般只讨论时间维度。算法复杂度就是算法使用的指令条数。这样我们就能对一个算法的效率做出评判标准了。在数据结构理论中算法复杂度的公式很复杂，主要依靠数学归纳推理的方式，这里就不展开讨论了。

有了算法之后，咱们第一个算法就来研究一下遍历算法。遍历算法就是将结构中的所有元素都访问一次。四种结构的遍历方法是不一样的。集合结构和线性结构的逻辑结构不复杂，物理结构直接顺序访问就可以了。树形结构和图形结构有层级关系，所以物理结构不是逻辑结构。产生了两种遍历方式，深度优先和广度优先。深度优先是优先遍历上下级关系，广度优先是优先遍历同级关系。这里又使用到了递归的概念。

我们主要关心线性结构和树形结构的遍历算法。线性结构遍历算法太简单，所以我们主要讨论树形结构遍历算法。树的遍历算法就是使用递归的方式，从根节点出发，重复遍历其子节点。有一种特殊的树叫二叉树，就是每个节点最多只有两个子节点。二叉树有很多特殊性质，大家自己慢慢研究。它最主要的特性在编码、排序和查找三个方面非常有用。所以我们需要重点学习二叉树的遍历算法。二叉树遍历有四种方式：前序遍历、中序遍历、后序遍历、层级遍历。分别对应了节点和子节点的输出顺序。

好了，我们讨论了这么久的算法和遍历，最终的目的是为了说明查找算法。在计算机程序中，查找数据结构中一个指定数据，这种需求非常多。比如在一个班级中查看张三的成绩。现实世界中，我们可以找到班主任，然后班主任在一堆学生成绩单中，顺序查找到张三的成绩。这种方式就是遍历查找，它有一个缺点，就是比较慢。如果成绩单按分数来进行排名，而我们知道张三的名次，老师查找成绩可以先拿中间的成绩，如果比张三名次高，老师再下半区间再取中间的成绩，这样逐步缩小查找范围，很快就能查找到张三的成绩。这种查找方式就是折半查找，前提需要数据元素是有序的。还有一种情况，老师能记住每个同学的成绩，直接通过张三的名字就立即知道了成绩。这种查找方式就是散列查找，每个成绩都有一个别名，直接返回结果。

总结一下查找算法有三种：遍历查找、折半查找、散列查找。遍历查找就是用遍历算法一个一个的查找。折半查找要求数据元素是有序的。散列查找要求每个元素有一个别名，就是我们常用的HashMap。

排序

我们已经理解了数据结构的逻辑结构、物理结构、结构变化、数据查找。数据查找中高效的折半查找算法要求数据元素是有序排列的，所以我们需要进一步研究如何进行排序。这里为了讨论方便，排序的数据元素是数字。因为数据元素由多个数据子项组成，只要有一个子项是数字就可以了。数字的排序就是指按数字大小进行升序或降序。

逻辑上我们要给10个数字进行排序，先找出最大值，然后在剩下的9个元素中再找出最大值，这样一直循环找出所有最大值。我们找10轮最大值就完成了对10个数字的排序，这种排序方法就是经典的冒泡排序。看上去也不是很难，但是事情往往没有我们表面上看到的这么简单。冒泡排序对数据量小的情况下非常好用，如果数据量达到上百万、上千万这样的情况时，就暴露了效率低下的问题，排序非常慢。

于是很多聪明的计算机大神们就开始寻找更加高效的排序算法。最终人们找到了一种快速排序算法，它能很好的解决这种大数据量的排序工作。我们简单的理解一下快速排序，它的主要思想是把数据通过平分的方式来缩小排序规模。怎么平分呢？还是刚刚10个数字的例子，先找出10个数字的中间值。我们就假设10个数字就是1到10，中间值就是5，小于5的分为A组，大于5的分为B组，AB两组中的元素是乱序的。我们再递归循环这样的过程，不停的再把AB组拆分成A1、A2和B1、B2。最终我们就能获得排序后的数据了。

快速排序的算法实现，大家自己慢慢研究。我们掌握这两种排序就可以了，冒泡排序和快速排序。我们要明白排序是为了查找效率更高。

总结

数据结构是一门非常复杂的学科，它涉及了多个学科的知识，比如数学、计算机硬件、编程、逻辑学等。所以数据结构要深入研究很难，特别是改进算法和创造算法。还好我们作为程序员主要的任务是解决业务问题，只需要理解逻辑上的数据结构和算法原理，能合理的运用已有的API工具就行了。在面对这种抽象的知识时，我们应该先从宏观上了解知识的概念，暂时不要关心证明和实现的过程，然后在掌握了已有知识工具的前提下，再回头来看看底层的原理。为了大家方便记忆数据结构的核心概念，我在下面做了知识点的总结。

知识点总结

数据结构的研究内容：逻辑结构、存储结构、操作（算法）。

逻辑结构有四种类型：集合结构、线性结构、树形结构、图形结构。

物理结构有两种类型：顺序存储、链式存储。

集合结构：哈希算法、无序、不重复。

线性结构：数组、链表、队列、栈。

树形结构：二叉树、深度优先、广度优先、递归。

图形结构：最短路径、关键路径。

数据关系

集合结构中数据关系是平等关系。
线性结构中数据关系是一对一关系。
树形结构中数据关系是一对多关系。
图形结构中数据关系是多对多关系。

数据操作类型：插入、删除、修改、查询、排序。