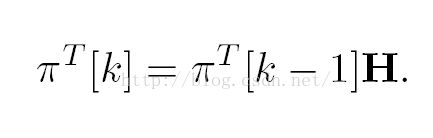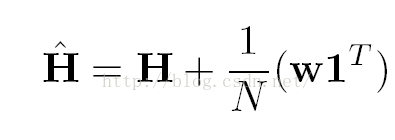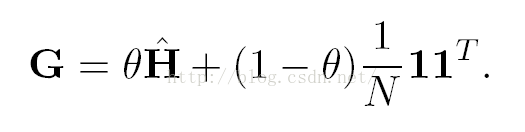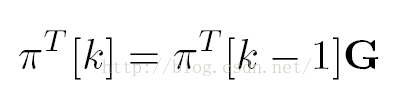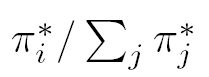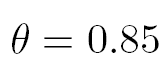Google PageRank算法解析
该算法早在十几年前就谷歌广泛应用在搜索引擎上
本文将讨论有关此算法的一些细节
首先附上我对Networked Life - 20 Questions and Answers这本本书引言的翻译内容,我认为这段用来引入话题再适合不过了
3.2
对于任何搜索引擎,有两个主要活动在持续不断进行
1. 在网页超链接中爬行以获得网页信息
2. 将此信息索引为简明的陈述和索引排序
当你使用谷歌搜索时,它会触发一个排名程序,这个程序需要考虑以下两个主要因素:
1. 每一个网页上内容的有多么相关,或叫相关性系数
2. 这个网页有多重要,或者叫重要性系数
这两个因素的综合得分决定了排名。我们把重点关注重要性系数排名,因为这在任何合理的热门搜索中,通常决定了前几页的排名,而这将巨大地影响人们如何获得信息的和在线电子商务如何保证信息流。
————————————————————————————————————————————————————————————————————————————
正文
PageRank算法是基于页面超连接的。我们假设网络中一共有N个页面。
迷途节点(Dangling Node)指的是没有任何向外超链接的网页节点
作为一个数学模型,我们需要有一个向量可以记录没有页面的重要性系数,我们假设这个向量是pai(一个只有1列N行的向量)
这个向量虽然说无所谓数值大小,只要能排序出区别就行,但是我们还是习惯于将其标准化为和等于1,因为这样相当于给所有页面一个分数的总量1
当然,我们还需要一个向量记录各个页面中超链接的指向情况,H
很明显H是一个N*N大小的向量,H(i,j)定义为,页面i到页面j有超链接,取值为1 / #out link(该页面的超链接数量);否自设为0
当分析这个矩阵的时候我们就可以看到,H的N行是第i个页面的超链接情况,H的列是第j页面被超链接情况
这个其实是在抽象一个不是非常完美的现实模型,就是我们假设用户访问每个页面时点击该页面的任意一个超链接的概率都是一样的,
而这个概率值乘以当前页面假设的重要性参数就是该页面分配给其超链接页面的分数
因此当页面的连接不再变化时,此模型会收敛于,即每个页面会有一个固定的重要性分数(根据其获得的分数)
2、PageRank是一种可以表示为马尔可夫链(Markov chain)的稳态概率分布
如果认真思考上述的模型会发现一个问题(或者说是bug)
从数学角度看,这个问题是有可能某页面没有任何超链接,那么这个页面在整个模型(迭代)中不会向外分享任何自己的重要性系数,整个模型会趋于所有页面的值都为0才能满足这个模型。就算这个页面同时没有被任何页面引用,那么这个页面的重要性将最终保持我们给它的初始值不变,这样看也是不合理的。
从行为学角度看,如果一个页面没有任何超链接,网友会直接放弃冲浪关掉浏览器么?还是说如果这个网页没有被任何其他页面引用,那么某人就不可能从另一个页面转到此页面?答案很明显是否定的。
因此,每个页面除了把所有的浏览概率分配给自己有超链接的页面外,还需要有一定概率给其他的页面。
这里需要分开讨论
a)首先是迷途节点情况,在这种情况下,我们应该强制要求这种页面分配自己的重要性分数给其他所有的页面,而分配量均与分布
b)对于所有的页面,应该有一定概率将包括自己没有超链接指向的所有页面,当然这个概率分配需要人为地设计
*需要注意上述a、b是相互独立的就是一定是先进性a再进行b
在解决上述问题后,我们可以就得到一个完整的马尔可夫链模型,而这种访问行为叫做random walk on graph(图的随机行走访问?)
PageRank模型不是完美的,但是一种复杂度和功能性之间的一种很好的平衡
k表示迭代次数,paiT是pai的转置,转置是因为我们关注的是在整个网络中页面收到的重要性得分量(标准化后体现为比例)
上图为每次更新新的pai*i的值(i指被指向的页面i)
另外,经过Google的大量实验,
是一个合理的取值
3、PageRank算法解决的不止迷途节点(Dangling Node)问题,而且还解决了最终连接块(final connected components)问题
最终连接块的意思是有几个网页,他们内部相互有超链接构成图。但是,这些页面的超连接没有一个是这些网页以外的。
也就是说如果吧这些页面看成一个整体,那么他们就像一个巨大的迷途节点,一旦通过超链接进入了这堆页面就无法通过超链接离开了
解决原理其实和迷途节点一样,就是添加强制的向外访问可能性,对应上述b小点