背包问题整理(持续更新)
多重背包
模板:

多重背包二进制优化:
用于多重背包问题中,一个物品可以放限制次的数量。
主体代码:
在使用时,分别讨论a[i]*b[i]<=m,其中a[i]为数量,b[i]为权值,m为上限,这时候使用二进制优化,当a[i]*b[i]>m时,使用正常多重背包模板,这样写时间更优化。
同时,也可以在输入的过程中使用二进制优化
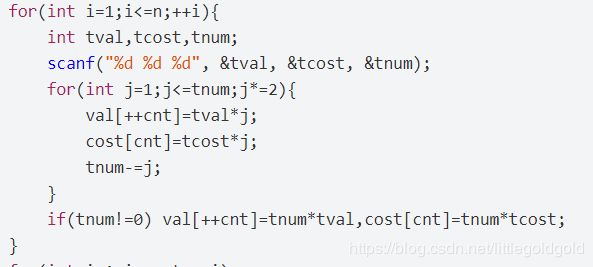
1.HDU2844 Coins(二进制优化)
#include这里面的主题转移函数,也可以这样下写:
memset(dp,-0x7f,sizeof(dp));
dp[0]=0;
转移方程:
dp[j]=max(dp[j],dp[j-k*a[i]]+k);
2.POJ1276 二进制优化
#include完全背包问题
每个物品可以取无限次,有一定的空间限制,取最优
(同样也可以转化为0/1背包问题,使用二进制优化)
模板:

1.CF543A Writing Code
完全背包问题,转化为有多种物品,每个物品各有重量,可以放无限次,要求刚好放入n件物品,且重量小于m 的方案数
理解了dp[i][j]这个题目就好做了,表示已经写了i行代码产生j个bug数的方案数量
#include2.CF189A Cut Ribbon
将一根长度为n的绳子分成只由a.b.c长度组成的子绳子。
完全背包问题 考虑到必须要能够正好由a.b.c拼凑出n
在完全背包中加入条件
if(dp[j-w[i]]!=0||j-w[i]==0)
dp[j]=max(dp[j],1+dp[j-w[i]]);
#include3.HDU1114 Piggy-Bank
刚好完全背包问题
#include01背包问题
模板:
三种写法:
一维数组:
for(int i=0;i<n;i++)
{
for(int j=m;j>=thing[i].first;j--)
{
dp[j]=max(dp[j],dp[j-thing[i].first]+thing[i].second);
}
}
二维数组:
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(j>=thing[i].first)
dp[i][j]=max(dp[i][j],dp[i-1][j-thing[i].first]+thing[i].second);
else
dp[i][j]=dp[i-1][j];
}
}
递归+记忆化:
int package(int index,int w)
{
if(index==0||w<=0)
return 0;
if(dp[index][w]!=0)
return dp[index][w];
//不放第index件物品
int res=package(index-1,w);
//放第index件物品
if(w>=thing[index].first)
res=max(res,package(index-1,w-thing[index].first)+thing[index].second);
dp[index][w]=res;
return res;
}
关于初始化的细节问题:
①要求恰好装满背包,那么在初始化时除了 F[0] 为 0,其它 F[1…V ] 均设为 −∞,这样就可以保证最终得到的 F[V ] 是一种恰好装满背包的最优解。
②如果并没有要求必须把背包装满,而是只希望价格尽量大,初始化时应该将 F[0…V ] 全部设为 0。
1.POJ3624 http://poj.org/problem?id=3624
一维DP数组
#include二维DP数组:这种会超内存,就当个参考
#include=thing[i].first;j--)
{
dp[j]=max(dp[j],dp[j-thing[i].first]+thing[i].second);
}
}
int ans=0;
for(int j=m;j>=0;j--)
ans=max(ans,dp[j]);*/
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(j>=thing[i].first)
dp[i][j]=max(dp[i][j],dp[i-1][j-thing[i].first]+thing[i].second);
else
dp[i][j]=dp[i-1][j];
}
}
int ans=0;
for(int j=1;j<=m;j++)
{
ans=max(dp[n][j],ans);
}
cout<<ans<<endl;
return 0;
}