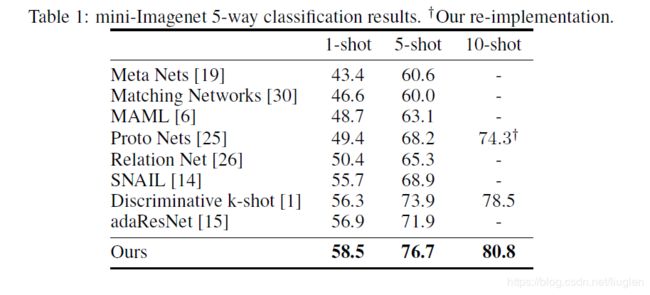
TADAM:Task dependent adaptive metric for improved few-shot learning
本文基于度量学习,发现简单的度量尺度会完全改变少样本学习参数更新的本质,同时提出了一个简单且有效的任务依赖的度量空间学习方法,可以根据不同的任务进行特征提取。通过度量缩放的方式,作者将余弦相似度与欧拉距离在少样本学习上的差距缩小了10%,也就是说度量的选择没有那么重要。另外,还提出了辅助任务协同训练,使得具有任务依赖性的特征提取更容易训练,并且具有很好的泛化能力
背景
考虑episodic形式的K-shot,C-way的分类问题
- sample(support) set S = { ( x i , y i ) } i = 1 K C \mathcal{S}=\{(x_i,y_i)\}_{i=1}^{KC} S={(xi,yi)}i=1KC,样本集,C类每类K个样本
- query set Q = ( x i , y i ) i = 1 q \mathcal{Q}={(x_i,y_i)}_{i=1}^q Q=(xi,yi)i=1q,待分类样本
- 相似度度量d: R 2 D z → R \mathbb{R}^{2D_z} \rightarrow\mathbb{R} R2Dz→R,d不需要满足一般度量的性质(非负,对称,可加性),Dz表示特征提取后的维度, f ϕ : R D x → r D z f_{\phi}:\mathbb{R}^{D_x}\rightarrow\mathbb{r}^{D_z} fϕ:RDx→rDz
- 为属于 S k \mathcal{S_k} Sk每一个类别k中的所有样本找到一个唯一的特征表示 c k c_k ck, c k = 1 K ∑ x i ∈ S k f ϕ ( x i ) c_k=\frac{1}{K}\sum_{x_i\in S_k}f_{\phi}(x_i) ck=K1∑xi∈Skfϕ(xi)
- 损失函数:最小化 − log p ϕ ( y = k ∣ x ) -\log p_{\phi}(y=k|x) −logpϕ(y=k∣x), p ϕ ( y = k ∣ x ) = s o f t m a x ( − d ( f ϕ , c k ) ) p_{\phi}(y=k|x)=softmax(-d(f_{\phi},c_k)) pϕ(y=k∣x)=softmax(−d(fϕ,ck))
模型
1.度量尺度
作者发现使用欧式距离分类表现更好的原因主要是度量的尺度不同,而且,输出的维度对输出具有直接的影响。假设 z ∼ N ( 0 , I ) , E z [ ∣ ∣ z ∣ ∣ 2 2 ] = D f z\sim\mathcal{N}(0,I),\mathbb{E}_z[||z||^2_2]=D_f z∼N(0,I),Ez[∣∣z∣∣22]=Df,如果 D f D_f Df很大,网络就必须在优化策略之外工作以便于缩小特征表示的范围,因此提出了可学习的参数 α \alpha α, p ϕ , α ( y = k ∣ x ) = s o f t m a x ( − α d ( z , c k ) ) p_{\phi,\alpha}(y=k|x)=softmax(-\alpha d(z,c_k)) pϕ,α(y=k∣x)=softmax(−αd(z,ck)),使得模型对不同的度量都可以有好的表现。对每种类别的交叉熵损失函数如下:
J k ( ϕ , α ) = ∑ x i ∈ Q k [ α d ( f ϕ ( x i ) , c k ) + log ∑ j e x p ( − α d ( f ϕ ( x i ) , c j ) ) ] {J}_k(\phi,\alpha)=\sum_{x_i\in\mathcal{Q}_k}[\alpha d(f_\phi(x_i),c_k)+\log{\sum_j}exp(-\alpha d(f_\phi(x_i),c_j))] Jk(ϕ,α)=xi∈Qk∑[αd(fϕ(xi),ck)+logj∑exp(−αd(fϕ(xi),cj))]
Q k = { ( x i , y i ) ∈ Q : y i = k } \mathcal{Q}_k=\{(x_i,y_i)\in\mathcal{Q}:y_i=k\} Qk={(xi,yi)∈Q:yi=k}是类别k的query set,对参数 ϕ \phi ϕ求梯度:
∂ ∂ ϕ J k ( ϕ , α ) = α ∑ x i ∈ Q k [ ∂ ∂ ϕ d ( f ϕ ( x i ) , c k ) − ∑ j e x p ( − α d ( f ϕ ( x i ) , c j ) ) ∂ ∂ ϕ d ( f ϕ ( x i ) , c k ) ∑ j e x p ( − α d ( f ϕ ( x i ) , c j ) ) ] \frac{\partial}{\partial\phi}J_k(\phi,\alpha)=\alpha\sum_{x_i\in \mathcal{Q}_k}[\frac{\partial}{\partial\phi}d(f_\phi(x_i),c_k)-\frac{{\sum_j}exp(-\alpha d(f_\phi(x_i),c_j))\frac{\partial}{\partial\phi}d(f_\phi(x_i),c_k)}{{\sum_j}exp(-\alpha d(f_\phi(x_i),c_j))}] ∂ϕ∂Jk(ϕ,α)=αxi∈Qk∑[∂ϕ∂d(fϕ(xi),ck)−∑jexp(−αd(fϕ(xi),cj))∑jexp(−αd(fϕ(xi),cj))∂ϕ∂d(fϕ(xi),ck)]
考虑 α \alpha α的极限情况对梯度的影响
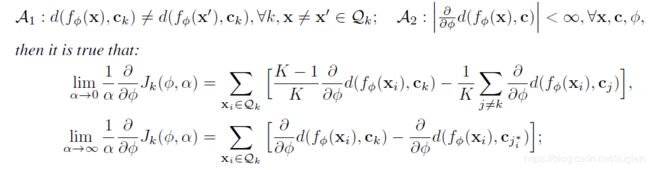
j i ∗ = a r g m i n j d ( f ϕ ( x i ) , c j ) j_i^* = argmin_jd(f_\phi(x_i),c_j) ji∗=argminjd(fϕ(xi),cj)
可以发现,
- α \alpha α较小时,第一项最小化了query的样本和他们对应的原型之间的特征距离,第二项最大化了query的样本和他们不属于的类别原型之间的特征距离
- α \alpha α较大时,第一项和上面的作用相同,第二项最大化了样本被错误分配的距离最近原型的距离
- 如果 j ∗ = k j^*=k j∗=k,意味着没有错误, x i x_i xi对于参数更新贡献为0,等价于只从导致分配错误的最明显的样本学习
- 这两种 α \alpha α的取值策略要么最小化样本分布的重叠,要么根据样本修正簇间分配;所以较大的取值可以更直接解决少样本的分类错误,但是随着优化的进行,可能有很多样本求出的梯度为0,优化进行的就会很慢,不过又通过实验证明了针对每个数据集和度量是存在一个最优的 α \alpha α
2.任务依赖

定义动态的特征提取器 f ϕ ( x , Γ ) f_\phi(x,\Gamma) fϕ(x,Γ), Γ \Gamma Γ是从任务表示中学习的学习的参数集合,所以特征提取器通过task的sample set S进行优化。
形式上, h l + 1 = γ ⊙ h l + β h_{l+1}=\gamma\odot h_l+\beta hl+1=γ⊙hl+β, γ , β \gamma,\beta γ,β 分别是作用于l层的缩放和偏移向量;具体地,使用类原型的均值作为任务表示, c ˉ = 1 c ∑ k c k \bar{c} = \frac{1}{c}\sum_k c_k cˉ=c1∑kck,即©中的TEN的输入,针对每个卷积层中得到不同的 γ , β \gamma,\beta γ,β。
TEN使用两个分开的全连接残差网络生成这两个向量,增加了 L 2 L_2 L2范数的惩罚项 γ 0 , β 0 \gamma_0,\beta_0 γ0,β0,可以限制 γ , β \gamma,\beta γ,β的效果,作者说有个原则是向量中的每一个元素应该是同时趋近于0的,除非任务条件作用对这层提供了明显的信息增益。
β = β 0 g θ ( c ˉ ) , γ = γ 0 h ϕ ( c ˉ ) + 1 \beta = \beta_0 g_\theta(\bar{c}),\gamma=\gamma_0h_\phi(\bar{c})+1 β=β0gθ(cˉ),γ=γ0hϕ(cˉ)+1
并且,TEN对于特征提取器中的每层的影响应该是不均匀的,靠近度量的层受到的条件限制应该比靠近图像的层大,因为浅层网络提取的像素级别的特征不具有任务特异性
3.总体结构
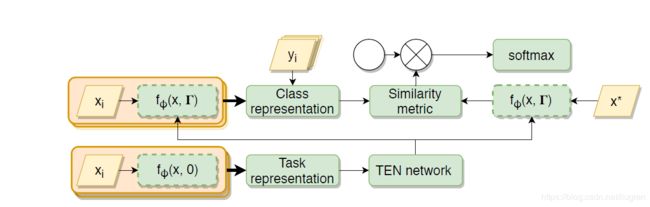
使用ResNet-12作为特征提取网络。训练分为两步,第一步遍历sample set,TEN针对每一个卷积层预测 α , β \alpha,\beta α,β的值,之后使用刚刚生成的 α , β \alpha,\beta α,β对sample set和query set进行特征提取。选择相似度度量找到每个query的实例对应的原型类别,最后将度量的输出使用 α \alpha α进行缩放并输入softmax层
4.辅助任务共训练
由于TEN网络的加入,同时学习TEN的有用特征和主要特征器是很困难的,会陷入局部最优解,使得使用任务条件的效果可能不如不使用。所以,使用mini-ImageNet上的64分类作为辅助任务(从训练集中随机均匀的抽取固定batch的64个图片样本),抽样概率随着episode指数衰减。
通过实验证明,使用辅助任务比预训练特征提取器更有效,作者把这个归功于辅助任务和主要任务在反向传播过程中梯度的共同影响。
辅助任务相当于是不适用任务条件之前的特征提取任务,所以相对来讲更简单,可以帮助学习器通过掌握最低的技能水平进而解决更困难的少样本分类问题。