Java 有向图的遍历，寻找所有从起点到终点的路径

最近遇到一个绘图的需求，是对地图的二次开发，在上面绘制覆盖物，所以这里涉及了对有向无环图的遍历问题。

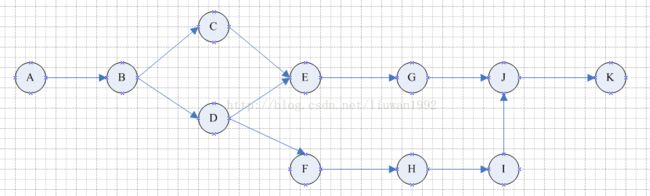
如下图是一个有向无环图：

正常的深度优先遍历算法得到的结果会是：A、B、C、E、G、J、K、D、F、H、I 。

但是我们需要的结果是：A、B、C、E、G、J、K ，A、B、D、E、G、J、K ，A、B、D、F、H、I、J、K 一共三条路径。

所以需要对普遍的深度优先遍历算法做一定修改，下面是完整代码：

public class Graph {
	// 邻接矩阵
	private double[][] matrix;
	// 顶点数组
	private T[] vertex;
	// 顶点的数目
	private int vertexNum;
	// 当前结点是否还有下一个结点，判断递归是否结束的标志
	private boolean noNext = false;
	// 所有路径的结果集
	private List> result = new ArrayList<>();

	public Graph(double[][] matrix, T[] vertex) {
		if (matrix.length != matrix[0].length) {
			throw new IllegalArgumentException("该邻接矩阵不是方阵");
		}
		if (matrix.length != vertex.length) {
			throw new IllegalArgumentException("结点数量和邻接矩阵大小不一致");
		}
		this.matrix = matrix;
		this.vertex = vertex;
		vertexNum = matrix.length;
	}

	/**
	 * 深度遍历的递归
	 */
	private void DFS(int begin, List path) {
		// 将当前结点加入记录队列
		path.add(vertex[begin]);
		// 标记回滚位置
		int rollBackNum = -1;
		// 遍历相邻的结点
		for (int i = 0; i < vertexNum; i++) {
			if ((matrix[begin][i] > 0)) {
				// 临时加入相邻结点，试探新的路径是否已遍历过
				path.add(vertex[i]);
				if (containBranch(result, path)) {
					// 路径已存在，将相邻结点再移出记录队伍
					path.remove(vertex[i]);
					// 记录相邻点位置，用于循环结束发现仅有当前一个相邻结点时回滚事件
					rollBackNum = i;
					// 寻找下一相邻结点
					continue;
				} else {
					// 路径为新路径，准备进入递归，将相邻结点移出记录队伍，递归中会再加入，防止重复添加
					path.remove(vertex[i]);
					// 递归
					DFS(i, path);
				}
			}
			// 终止递归
			if (noNext) {
				return;
			}
		}
		if (rollBackNum > -1) {
			// 循环结束仅有一个相邻结点，从这个相邻结点往下递归
			DFS(rollBackNum, path);
		} else {
			// 当前结点没有相邻结点，设置flag以结束递归
			noNext = true;
		}
	}

	/**
	 * 开始深度优先遍历
	 */
	public List> startSearch() {
		for (int i = 0; i < countPathNumber(); i++) {
			// 用于存储遍历过的点
			List path = new LinkedList<>();
			noNext = false;
			// 开始遍历
			DFS(0, path);
			// 保存结果
			result.add(path);
		}
		return result;
	}

	/**
	 * 计算路径的分支数量
	 */
	private int countPathNumber() {
		int[] numberArray = new int[vertexNum];
		for (int i = 0; i < vertexNum; i++) {
			for (int j = 0; j < vertexNum; j++) {
				if (matrix[j][i] > 0) {
					numberArray[j]++;
				}
			}
		}
		int number = 1;
		for (int k = 0; k < vertexNum; k++) {
			if (numberArray[k] > 1) {
				number++;
			}
		}
		return number;
	}

	/**
	 * 判断当前路径是否被已有路径的结果集合所包含
	 */
	private boolean containBranch(List> nodeLists, List edges) {
		for (int i = 0; i < nodeLists.size(); i++) {
			List list = nodeLists.get(i);
			if (list.containsAll(edges)) {
				return true;
			}
		}
		return false;
	}

}

下面是一个测试类：

public class Test {
	
    public static void main(String[] args) {
    	String[] vertex = { "a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k" };
		double[][] matrix = { 
				{ 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
				{ 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0 },
				{ 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0 },
				{ 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0 },
				{ 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0 },
				{ 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0 },
				{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0 },
				{ 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0 },
				{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0 },
				{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1 },
				{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 } };
		
        Graph graph = new Graph<>(matrix, vertex);
        System.out.println(graph.startSearch());
    }
    
}

运行结果如下图：

从上图可以看出达到了我们想要的结果，如果有什么不对的请指正。后期还可以对方法进行修改，可以将 1 改为路径长度，计算一

定长度的路径，也可以计算点到点的路径。