sklearn.preprocessing数据预处理分析（正则化标准化归一化）

sklearn.preprocessing用于对数据进行预处理，具体有缩放、转换和归一

1. 数据说明

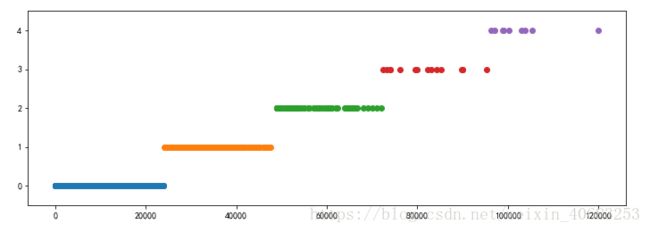
每一行表示一个样本，每一列表示一个特征

import numpy as np
from sklearn.preprocessing import *
X = np.array([[1., -1., 2.],
              [2., 0., 0.],
              [0., 1., -1.]])

测试效果的数据如图，左边为原始数据（横轴为收入纵轴为家庭数），右边为经过处理的数据，该数据含有少量不超过边界的离群值（异常值）

2. 标准化Standardization

2.1 MinMaxScaler 最大最小值缩放

作用：
将特征值缩放到给定的最大最小值之间

目的：

1. 实现特征极小方差的鲁棒性
2. 在稀疏矩阵中保留零元素

代码：

X = np.array([[1., -1., 2.],
              [2., 0., 0.],
              [0., 1., -1.]])
print(MinMaxScaler().fit_transform(X))  # 最大最小值缩放
"""
[[0.5        0.         1.        ]
 [1.         0.5        0.33333333]
 [0.         1.         0.        ]]
"""

公式：
$$scale=\frac{max-min}{\text{X.}\max -\text{X.}\min }$$
$scale$为缩放比例，其中$max$和$min$为给定的最大最小值，X.max和X.min为数据的最大最小值

$$\text{X}scaled=scale\cdot \left(\text{X}-\text{X.}\min \right)$$
$\text{X}scale$为缩放后的结果

data = [[-1, 2],
        [-0.5, 6],
        [0, 10],
        [1, 18]]
scaler = MinMaxScaler()  # 给定的max为1，min为0
scaler.fit(data)
print(scaler.data_max_)  # [ 1. 18.]
print(scaler.data_min_)  # [-1.  2.]
print(scaler.scale_)  # [0.5 0.0625] 等价于1/[2. 16.]
print(scaler.transform(data))
"""
[[0.   0.  ]
 [0.25 0.25]
 [0.5  0.5 ]
 [1.   1.  ]]
"""

$$scale=\frac{max-min}{\text{X.}\max -\text{X.}\min }=\frac{1-0}{\left(\begin{array}{cc}1.& 18.\end{array}\right)-\left(\begin{array}{cc}-1.& 2.\end{array}\right)}=\frac{1}{\left(\begin{array}{cc}2.& 16.\end{array}\right)}=\left(\begin{array}{cc}0.5& 0.0625\end{array}\right)$$
代入$$\left(\begin{array}{cc}-0.5& 6.\end{array}\right)$$
得
$$\text{X}scaled=scale\cdot \left(\text{X}-\text{X.}\min \right)=\left(\begin{array}{cc}0.5& 0.0625\end{array}\right)\cdot \left(\left(\begin{array}{cc}-0.5& 6.\end{array}\right)-\left(\begin{array}{cc}-1.& 2.\end{array}\right)\right)=\left(\begin{array}{cc}0.25& 0.25\end{array}\right)$$

效果
作为标准化缩放器，MinMaxScaler对异常值（离群值）非常敏感

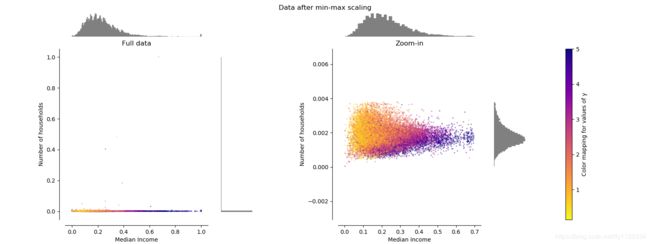
2.2 MaxAbsScaler 最大绝对值缩放

作用
将特征值缩放到给定的最大值矩形区域之间，如[-1, 1]

目的
与MaxAbsScaler类似，且训练数据应是已经零中心化或者是稀疏数据

代码

X = np.array([[1., -1., 2.],
              [2., 0., 0.],
              [0., 1., -1.]])
print(MaxAbsScaler().fit_transform(X))  # 最大绝对值缩放
"""
[[ 0.5 -1.   1. ]
 [ 1.   0.   0. ]
 [ 0.   1.  -0.5]]
"""

公式
与MaxAbsScaler类似
效果
作用在绝对值数据上的效果和MinMaxScaler一样，同样对异常值敏感

2.3 RobustScaler 鲁棒缩放

作用
当数据有许多异常值可用来替代MinMaxScaler和MaxAbsScaler
代码

print(RobustScaler().fit_transform(X))  # 鲁棒缩放
"""
[[ 0.         -1.          1.33333333]
 [ 1.          0.          0.        ]
 [-1.          1.         -0.66666667]]
"""

X = [[ 1., -2.,  2.],
     [ -2.,  1.,  3.],
     [ 4.,  1., -2.]]
transformer = RobustScaler().fit(X)
print(transformer.transform(X))
"""
[[ 0.  -2.   0. ]
 [-1.   0.   0.4]
 [ 1.   0.  -1.6]]
"""

效果
不像MinMaxScaler和MaxAbsScaler，该缩放器基于百分比，因此不会受少量严重离群值的干扰。同时，得到的特征结果范围会比上述两个缩放器大，而且数据更趋向于相似。
注意，离群值仍然会被进行转换。对单独的离群点裁剪，则需要进行非线性转换。

3. 非线性转换

3.1 QuantileTransformer 均匀分布转换

作用
将数据无参数地映射到0到1的均匀分布上
代码

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
quantile_transformer = QuantileTransformer(random_state=0)
X_train_trans = quantile_transformer.fit_transform(X_train)
X_test_trans = quantile_transformer.transform(X_test)
print(np.percentile(X_train[:, 0], [0, 25, 50, 75, 100]))  # 获取第0%、第25%等等的值 [4.3 5.1 5.8 6.5 7.9]
print(np.percentile(X_train_trans[:, 0], [0, 25, 50, 75, 100]))  # [0. 0.23... 0.50... 0.74... 1. ]

效果
将特征值映射到均匀分布上，此为[0, 1]
无法区分异常值，不同于RobustScaler，QuantileTransformer通过将异常值设为规定的范围值来达到消除异常值的目的。

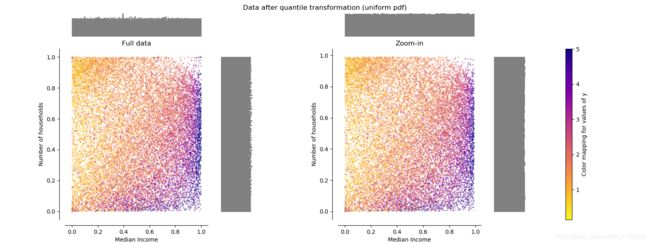
3.2 PowerTransformer 高斯分布转换

作用
将数据从任何分布映射到尽可能接近高斯分布
幂变换是一类参数化的单调变换，通过幂变换实现。
目的

1. 稳定方差
2. 最小化偏度

公式
该方法提供了两种幂变换Yeo-Johnson transform和Box-Cox transform

Yeo-Johnson transform公式如下：

Box-Cox transform公式如下，且数据必须为正：

这两种幂变换都是参数化的，该参数由极大似然估计确定

pt = PowerTransformer(method='box-cox', standardize=False)
X_lognormal = np.random.RandomState(616).lognormal(size=(3, 3))  # 对数正态分布
print(X_lognormal)
print(pt.fit_transform(X_lognormal))  # 映射为正态分布
"""
[[1.28... 1.18... 0.84...]
 [0.94... 1.60... 0.38...]
 [1.35... 0.21... 1.09...]]
[[ 0.49...  0.17... -0.15...]
 [-0.05...  0.58... -0.57...]
 [ 0.69... -0.84...  0.10...]]
"""

默认情况下，standardize=True，即会应用零均值化和单位方差归一化

效果
下面是将不同概率分布分别应用幂转换达到映射到高斯分布的效果。有些非常像高斯分布，有些则不然，因此做数据可视化是很有必要的。

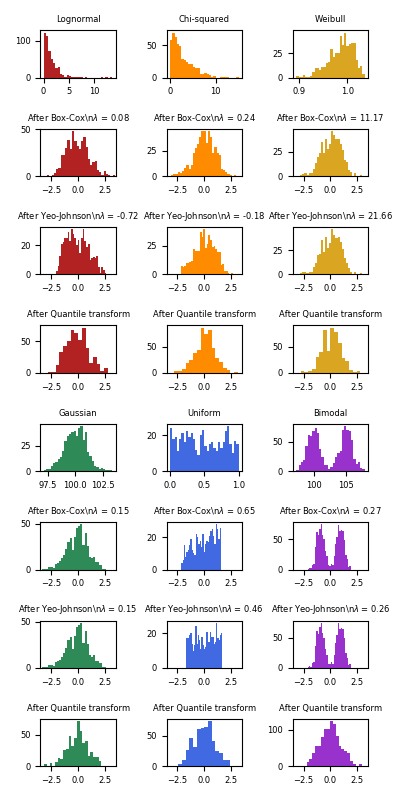
Yeo-Johnson transform

Box-Cox

4. 归一化Normalization

4.1 normalize 归一化

作用
将特征值缩放以具有单位范数

目的
经常在文本分类和内容聚类中使用

代码
l1范式

X = np.array([[1., -1., 2.],
              [2., 0., 0.],
              [0., 1., -1.]])
print(normalize(X, norm='l1')) # l1范式归一化
"""
[[ 0.25 -0.25  0.5 ]
 [ 1.    0.    0.  ]
 [ 0.    0.5  -0.5 ]]
"""              

l2范式

X = np.array([[1., -1., 2.],
              [2., 0., 0.],
              [0., 1., -1.]])
print(normalize(X, norm='l2')) # l2范式归一化
"""
[[ 0.40... -0.40...  0.81...]
 [ 1.       0.       0.     ]
 [ 0.       0.70... -0.70...]]
"""              

公式
效果
所有样本被映射到单位圆中

5. 编码类别

5.1 OrdinalEncoder 哑编码

作用
有时候特征不是连续值而是间断值，例如一个人的性别的值域为["male", "female"]，国籍的值域为["from Europe", "from US", "from Asia"]，常用浏览器的值域为["uses Firefox", "uses Chrome", "uses Safari", "uses Internet Explorer"]。
则['male', 'from US', 'uses Safari']和['female', 'from Europe', 'uses Firefox']这两个人用[0, 1, 2]和[1, 0, 0]表示。

代码

enc = OrdinalEncoder()
X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
enc.fit(X)
print(enc.transform([['female', 'from US', 'uses Safari']]))  # [[0. 1. 1.]]

5.2 OneHotEncoder 独热编码

作用
将每一个类可能取值的特征变换为二进制特征向量，每一类的特征向量只有一个地方是1，其余位置都是0

代码

1. 自动推断类别

enc = OneHotEncoder()
X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
enc.fit(X)
print(enc.categories_)
"""[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object), array(['uses Firefox', 'uses Safari'], dtype=object)]"""
print(enc.get_feature_names())
"""['x0_female' 'x0_male' 'x1_from Europe' 'x1_from US' 'x2_uses Firefox' 'x2_uses Safari']"""
print(enc.transform([['female', 'from US', 'uses Safari'],
                     ['male', 'from Europe', 'uses Safari']]).toarray())
"""
[[1. 0. 0. 1. 0. 1.]
 [0. 1. 1. 0. 0. 1.]]
"""

可以看出性别、国籍、常用浏览器均有两个值可选，那么每两个值为一类。例如[1. 0. 0. 1. 0. 1.]，前两个值[1. 0.]为female，中两个值[0. 1.]为from US，后两个值[0. 1.]为uses Safari

2. 手动设置类别

genders = ['female', 'male']
locations = ['from Africa', 'from Asia', 'from Europe', 'from US']
browsers = ['uses Chrome', 'uses Firefox', 'uses IE', 'uses Safari']
enc = OneHotEncoder(categories=[genders, locations, browsers])
X = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox']]
enc.fit(X)
print(enc.get_feature_names())
"""['x0_female' 'x0_male' 'x1_from Africa' 'x1_from Asia' 'x1_from Europe' 'x1_from US' 'x2_uses Chrome' 'x2_uses Firefox' 'x2_uses IE' 'x2_uses Safari']"""
print(enc.transform([['female', 'from Asia', 'uses Chrome']]).toarray())
"""[[1. 0. 0. 1. 0. 0. 1. 0. 0. 0.]]"""

新建OneHotEncoder对象时设置handle_unknown='ignore'可以忽略未知的特征值而不会抛出任何错误

6. 离散化Discretization

6.1 KBinsDiscretizer K-bins等宽离散化

作用
将连续特征值划分为离散特征值，等宽分为K个区间，并把值对应放置在不同区间上，输出经过独热编码

代码

X = np.array([[ -3., 5., 15 ],
              [  0., 6., 14 ],
              [  6., 3., 11 ]])
est = KBinsDiscretizer(n_bins=[3, 2, 2], encode='ordinal').fit(X)
print(est.transform(X))
"""
[[0. 1. 1.]
 [1. 1. 1.]
 [2. 0. 0.]]
"""

特征1：$\left[-\infty ,-1\right),\left[-1,2\right),\left[2,\infty \right)$
特征2：$\left[-\infty ,5\right),\left[5,\infty \right)$
特征3：$\left[-\infty ,14\right),\left[14,\infty \right)$

效果

6.2 Binarizer 二值化

作用
将特征值用阈值过滤得到布尔值

代码

X = np.array([[1., -1., 2.],
              [2., 0., 0.],
              [0., 1., -1.]])
print(Binarizer().fit_transform(X))  # 二值化，默认阈值为0
"""
[[1. 0. 1.]
 [1. 0. 0.]
 [0. 1. 0.]]
"""

X = np.array([[1., -1., 2.],
              [2., 0., 0.],
              [0., 1., -1.]])
print(Binarizer(threshold=1.1).fit_transform(X))  # 二值化，设阈值为1.1
"""
[[0. 0. 1.]
 [1. 0. 0.]
 [0. 0. 0.]]
"""

7. 生成多项式特征

7.1 PolynomialFeatures 生成多项式特征

作用
将特征与特征相乘，生成多项式特征

目的
增加模型复杂度

代码

import numpy as np
X = np.arange(6).reshape(3, 2)
print(X)
"""
[[0 1]
 [2 3]
 [4 5]]
"""
poly = PolynomialFeatures(2)
print(poly.fit_transform(X))
"""
[[ 1.  0.  1.  0.  0.  1.]
 [ 1.  2.  3.  4.  6.  9.]
 [ 1.  4.  5. 16. 20. 25.]]
"""

$X$的特征从$\left(X_1,X_2\right)$转换为$\left(1,X_1,X_2,X_1^2,X_1{X}_2,X_2^2\right)$

设置interaction_only=True表示只需要特征间的交互项

import numpy as np
X = np.arange(9).reshape(3, 3)
print(X)
"""
[[0 1 2]
 [3 4 5]
 [6 7 8]]
"""
poly = PolynomialFeatures(degree=3, interaction_only=True)
print(poly.fit_transform(X))
"""
[[  1.   0.   1.   2.   0.   0.   2.   0.]
 [  1.   3.   4.   5.  12.  15.  20.  60.]
 [  1.   6.   7.   8.  42.  48.  56. 336.]]
"""

$X$的特征从$\left(X_1,X_2,X_3\right)$转换为$\left(1,X_1,X_2,X_3,X_1{X}_2,X_1{X}_3,X_2{X}_3,X_1{X}_2{X}_3\right)$

API查阅

__all__ = [
    'Binarizer', # 二值化
    'FunctionTransformer',
    'Imputer',
    'KBinsDiscretizer', # 等宽离散化
    'KernelCenterer',
    'LabelBinarizer',
    'LabelEncoder',
    'MultiLabelBinarizer',
    'MinMaxScaler', # 最大最小值缩放
    'MaxAbsScaler', # 最大绝对值缩放
    'QuantileTransformer', # 均匀分布转换
    'Normalizer', # 归一化
    'OneHotEncoder', # 独热编码
    'OrdinalEncoder', # 哑编码
    'PowerTransformer', # 高斯分布转换
    'RobustScaler', # 鲁棒缩放
    'StandardScaler',
    'add_dummy_feature',
    'PolynomialFeatures', # 生成多项式特征
    'binarize', # 二值化
    'normalize', # 归一化
    'scale',
    'robust_scale', # 鲁棒缩放
    'maxabs_scale', # 最大绝对值缩放
    'minmax_scale', # 最大最小值缩放
    'label_binarize',
    'quantile_transform', # 均匀分布转换
    'power_transform', # 高斯分布转换
]

参考文献

1. sklearn.preprocessing官方文档
2. sklearn.preprocessing中文文档
3. 不同方法在一个包含边缘离群值的数据集中的表现
4. 使用sklearn做单机特征工程
5. 预处理数据的方法总结（使用sklearn-preprocessing）
6. 数据离散化 - 等宽&等频&聚类离散

作用
目的
代码
公式
效果