快速傅立叶变换FFT与快速数论变换NTT
FFT与NTT
在详细讲解FFT的内容之前,我们先主要回顾一下关于多项式和原根的相关内容:
多项式
系数表达式:若一个n次多项式 A ( x ) = a 0 + a 1 x + … + a n x n A(x)=a_0+a_1x+\ldots+a_nx^n A(x)=a0+a1x+…+anxn是由其系数 ( a 0 , a 1 , … , a n ) (a_0,a_1,\ldots,a_n) (a0,a1,…,an)唯一确定,则这种方式被称为多项式的系数表达形式。有时也被写为如下形式:
A ( x ) = ∑ i = 0 n a i x i A(x)=\sum_{i=0}^n a_ix^i A(x)=i=0∑naixi
点值表达式:若将多项式定义域内的任意一个值 x 0 x_0 x0代入上面的系数表达式,则可以得到多项式的值 y 0 y_0 y0。根据多项式插值的思想,一个多项式能够被至少n+1个不同的点 ( x i , y i ) , i ∈ { 0 , n } (x_i,y_i),i\in \{0,n\} (xi,yi),i∈{0,n}所唯一确定,这种方式被称为多项式的点值表达式。
单位根与原根
单位根
若想将多项式的系数表达式转化为点值表达式,我们需要取n+1个不同的点来进行计算,由于复平面上的1的原根具有很好的性质,且可以满足我们的要求,故将其作为介绍目标。形式化定义为: w n = 1 w^n=1 wn=1,记为 w n w_n wn。对于任意一个正整数n,有n个n次单位根恰好均匀分布在复平面单位圆上。
有欧拉恒等式可得 e π i + 1 = 0 e^{\pi i}+1=0 eπi+1=0,即 e π i = − 1 e^{\pi i}=-1 eπi=−1。则我们可以得到 e 2 π i = 1 e^{2\pi i}=1 e2πi=1。故我们令
w n k = e 2 k π i n = ( e 2 π i n ) k w_{n}^{k}=e^{\frac{2k\pi i}{n}}=(e^{\frac{2\pi i}{n}})^k wnk=en2kπi=(en2πi)k
具体例子如下图:
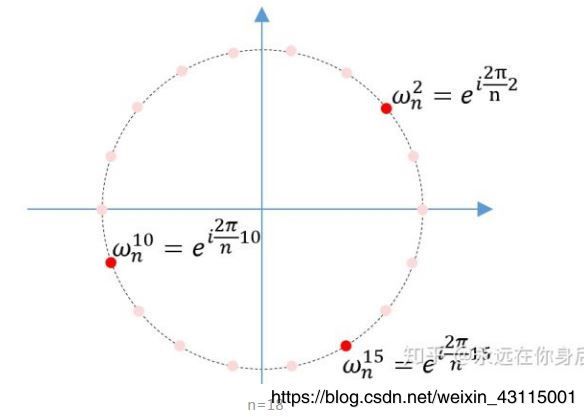
且关于单位根有下面三个重要的定理:
[1] w n k + n 2 = e 2 π i n ( k + n 2 ) = e 2 π i n k e π i = − e 2 π i n k = − w n k w_n^{k+\frac{n}{2}}=e^{\frac{2\pi i}{n}(k+\frac{n}{2})}=e^{\frac{2\pi i}{n}k}e^{\pi i}=-e^{\frac{2\pi i}{n}k}=-w_n^{k} wnk+2n=en2πi(k+2n)=en2πikeπi=−en2πik=−wnk
[2] w 2 n 2 k = w n k w_{2n}^{2k}=w_{n}^{k} w2n2k=wnk
[3] w n − k = 1 e 2 π i n ( − k ) = e 2 π i e 2 π i n ( − k ) = e 2 π i n ( n − k ) = w n n − k w_n^{-k}=1e^{\frac{2\pi i}{n}(-k)}=e^{2\pi i}e^{\frac{2\pi i}{n}(-k)}=e^{\frac{2\pi i}{n}(n-k)}=w_n^{n-k} wn−k=1en2πi(−k)=e2πien2πi(−k)=en2πi(n−k)=wnn−k
原根
【阶】若 r , n r,n r,n是互素的整数,且 r ≠ 0 , n > 0 r \neq0,n>0 r=0,n>0,使得等式 r x ≡ 1 ( m o d n ) r^x\equiv 1(mod~n) rx≡1(mod n)成立的最小正整数 x x x称为 r r r模 n n n的阶,通常记为 O r d n ( r ) Ord_n(r) Ordn(r)。
【欧拉函数】假设 n n n是一个正整数,则它的欧拉函数就是小于 n n n且与 n n n互素正整数的个数,记为 ϕ ( n ) \phi(n) ϕ(n)。
【原根】若 r , n r,n r,n是互素的整数,且 r ≠ 0 , n > 0 r \neq0,n>0 r=0,n>0和 O r d n ( r ) = ϕ ( n ) Ord_n(r)=\phi(n) Ordn(r)=ϕ(n),则称 r r r是模 n n n的原根。
FFT
为了方便理解,假设我们的计算目标是C(x)=A(x)B(x),且多项式A(x)和B(x)分别是a,b。令n=a+b。
核心思想:利用拉格朗日插值的思想,实现多项式的系数表达式和点值表达式之间的转换。
主要工具:
离散傅立叶变换:(DFT)
X k = ∑ j = 0 n − 1 x j e 2 π i n k j X_k=\sum_{j=0}^{n-1}x_je^{\frac{2\pi i}{n}kj} Xk=j=0∑n−1xjen2πikj
离散傅立叶逆变换:(IDFT)
x j = 1 n ∑ k = 0 n − 1 X k e − 2 π i n j k x_j=\frac{1}{n}\sum_{k=0}^{n-1}X_ke^{-\frac{2\pi i}{n}jk} xj=n1k=0∑n−1Xke−n2πijk
具体步骤:
[1]:取n个单位根: w n 0 w_n^0 wn0, w n 1 w_n^1 wn1,…, w n n − 1 w_n^{n-1} wnn−1
[2]:将n个不同的单位根代入多项式 A ( x ) A(x) A(x)和 B ( x ) B(x) B(x),即计算 A ( w n k ) A(w_n^k) A(wnk)和 B ( w n k ) B(w_n^k) B(wnk)
[3]:计算 C ( w n k ) = A ( w n k ) B ( w n k ) C(w_n^k)=A(w_n^k)B(w_n^k) C(wnk)=A(wnk)B(wnk)
[4]:令 D ( x ) = C 0 + C 1 x 1 + … + C n − 1 x n − 1 D(x)=C_0+C_1x^1+\ldots+C_{n-1}x^{n-1} D(x)=C0+C1x1+…+Cn−1xn−1,并计算 D ( w n k ) D(w_n^k) D(wnk)
[5]:计算多项式 C ( x ) C(x) C(x)的系数 c j = 1 n D ( w n n − j ) c_j=\frac{1}{n}D(w_n^{n-j}) cj=n1D(wnn−j)
详细过程:由于第[1]、[3]步比较简单,我们直接跳过。
【2】计算 A ( w n k ) A(w_n^k) A(wnk)、 B ( w n k ) B(w_n^k) B(wnk)
最直接将n个单位根代入多项式,但是这样的时间复杂度比较高。故这里我们采用分治的思想来进行加速。举个例子:
假设有一个多项式 H ( x ) = h 0 + h 1 x 1 + h 2 x 2 + h 3 x 3 H(x)=h_0+h_1x^1+h_2x^2+h_3x^3 H(x)=h0+h1x1+h2x2+h3x3,将该多项式写成按奇偶项拆分成两个子多项式的和,则有:
H ( x ) = ( h 0 + h 2 x 2 ) + ( h 1 x 1 + h 3 x 3 ) = ( h 0 + h 2 x 2 ) + x ( h 1 + h 3 x 2 ) H(x)=(h_0+h_2x^2)+(h_1x^1+h_3x^3)=(h_0+h_2x^2)+x(h_1+h_3x^2) H(x)=(h0+h2x2)+(h1x1+h3x3)=(h0+h2x2)+x(h1+h3x2)
H ( x ) = H 1 ( x 2 ) + x H 2 ( x 2 ) H(x)=H_1(x^2)+xH_2(x^2) H(x)=H1(x2)+xH2(x2)
若将这种思想用在计算 A ( w n k ) A(w_n^k) A(wnk)、 B ( w n k ) B(w_n^k) B(wnk)上,我们以计算 A ( w n k ) A(w_n^k) A(wnk)为例, 0 ≤ k < n 2 0\leq k <\frac{n}{2} 0≤k<2n,有:
当单位值在复平面单位圆的上部分时:
A ( w n k ) = A 1 ( w n 2 k ) + w n k A 2 ( w n 2 k ) = A 1 ( w n 2 k ) + w n k A 2 ( w n 2 k ) A(w_n^k)=A_1(w_n^{2k})+w_n^{k}A_2(w_n^{2k})=A_1(w_{\frac{n}{2}}^{k})+w_n^{k}A_2(w_{\frac{n}{2}}^{k}) A(wnk)=A1(wn2k)+wnkA2(wn2k)=A1(w2nk)+wnkA2(w2nk)
当单位值在复平面单位圆的下部分时:
A ( w n k + n 2 ) = A 1 ( w n 2 k + n ) + w n k + n 2 A 2 ( w n 2 k + n ) = A 1 ( w n 2 k ) − w n k A 2 ( w n 2 k ) = = A 1 ( w n 2 k ) − w n k A 2 ( w n 2 k ) A(w_n^{k+\frac{n}{2}})=A_1(w_n^{2k+n})+w_n^{k+\frac{n}{2}}A_2(w_n^{2k+n})=A_1(w_{n}^{2k})-w_n^{k}A_2(w_{n}^{2k})==A_1(w_{\frac{n}{2}}^{k})-w_n^{k}A_2(w_{\frac{n}{2}}^{k}) A(wnk+2n)=A1(wn2k+n)+wnk+2nA2(wn2k+n)=A1(wn2k)−wnkA2(wn2k)==A1(w2nk)−wnkA2(w2nk)
由此可见, k k k只需取一半范围的值就可以得到整个范围的计算结果。事实上,多项式 A 1 A_1 A1和 A 2 A_2 A2的计算可以利用分治的思想,这里明白即可,不再赘述。
【4】在计算 C ( w n k ) = A ( w n k ) B ( w n k ) C(w_n^k)=A(w_n^k)B(w_n^k) C(wnk)=A(wnk)B(wnk)之后,后面的主要工作是利用IDFT将 ( w n k , C ( w n k ) ) (w_n^k,C(w_n^k)) (wnk,C(wnk))转化为系数表达式,即求 c j c_j cj。为了方便描述和形式化表达,我们这里引入一个n-1次多项式 D ( x ) = C 0 + C 1 x 1 + … + C n − 1 x n − 1 = ∑ k = 0 n − 1 C k x k D(x)=C_0+C_1x^1+\ldots+C_{n-1}x^{n-1}= \sum_{k=0}^{n-1}C_kx^k D(x)=C0+C1x1+…+Cn−1xn−1=∑k=0n−1Ckxk,且 C k = C ( w n k ) C_k=C(w_n^k) Ck=C(wnk)已经在【3】步中计算完毕。
【5】由IDFT可得:
c j = 1 n ∑ k = 0 n − 1 C k e − 2 π i n j k = 1 n ∑ k = 0 n − 1 C k ( w n − j ) k = 1 n ∑ k = 0 n − 1 C k ( w n n − j ) k = 1 n D ( w n n − j ) c_j=\frac{1}{n}\sum_{k=0}^{n-1}C_ke^{-\frac{2\pi i}{n}jk}=\frac{1}{n}\sum_{k=0}^{n-1}C_k(w_n^{-j})^k=\frac{1}{n}\sum_{k=0}^{n-1}C_k(w_n^{n-j})^k=\frac{1}{n}D(w_n^{n-j}) cj=n1k=0∑n−1Cke−n2πijk=n1k=0∑n−1Ck(wn−j)k=n1k=0∑n−1Ck(wnn−j)k=n1D(wnn−j)
若将上述的过程中的 D ( x ) D(x) D(x)看作一个系数已知的多项式,其求 c j c_j cj的过程也可以使用分治的思想进行加速。
注意:关于DFT和IDFT的证明可以直接在网上搜索,比较简单,不进行叙述。
NTT
由于在密码学中,多项式的卷积并不是像FFT中的一样,它们往往是循环多项式的卷积,即在多项式的卷积后要模上一个大素数。故我们需要对FFT进行相应的改造,即NTT。
需要说明的是,在FFT中我们选取的是复平面的单位根,而在NTT中我们使用的是相应的原根。这是因为假设当 p p p是一个奇素数, g g g是模 n n n的原根,当 0 < i , j < p 0
给定模数 M = c ∗ 2 k + 1 M=c*2^k+1 M=c∗2k+1(这是满足密码学中多项式循环卷积的模数形式的)及其原根 g g g以及正整数 n = 2 l n=2^l n=2l(通常是多项式的次数),且 l ≤ k l\leq k l≤k,则有:
M − 1 = c ∗ 2 k M-1=c*2^k M−1=c∗2k
M − 1 n = c ∗ 2 k 2 l = c ∗ 2 k − l \frac{M-1}{n}=\frac{c*2^k}{2^l}=c*2^{k-l} nM−1=2lc∗2k=c∗2k−l
若令 a = g M − 1 n a=g^{\frac{M-1}{n}} a=gnM−1,则刚好能够构造出 n n n个 m o d M mod~M mod M不同值,满足 a i ≡ ( g M − 1 n ) i ≡ ( g M − 1 ) i n ≡ 1 ( m o d M ) a^i\equiv (g^{\frac{M-1}{n}})^i \equiv (g^{M-1})^{\frac{i}{n}}\equiv 1(mod~M) ai≡(gnM−1)i≡(gM−1)ni≡1(mod M)。
下面是原根满足的两个性质:
[1]: a n ≡ 1 ( m o d M ) a^n\equiv 1(mod~M) an≡1(mod M)
[2]: a n 2 ≡ − 1 ( m o d M ) a^{\frac{n}{2}}\equiv -1(mod~M) a2n≡−1(mod M)
主要工具:对于次数为 N = 2 l N=2^l N=2l(不足2的整数次幂的可以通过补0来扩张)且系数元素均小于 M M M的多项式系数序列 x ( n ) x(n) x(n), n n n表示第n个系数,有相应的快速数论变换:
快速数论变换:(NTT)
X ( m ) ≡ ∑ n = 0 N − 1 x ( n ) a m n m o d M X(m)\equiv \sum_{n=0}^{N-1}x(n)a^{mn} ~~~~~mod~M X(m)≡n=0∑N−1x(n)amn mod M
快速数论逆变换:(INTT)
x ( n ) = 1 N ∑ m = 0 N − 1 X ( m ) a − m n m o d M x(n)=\frac{1}{N}\sum_{m=0}^{N-1}X(m)a^{-mn} ~~~~~mod~M x(n)=N1m=0∑N−1X(m)a−mn mod M
蝶形操作:在FFT中,将多项式的系数表达式转化为点值表达式的过程中,我们主要采取分治的思想进行加速。而在NTT中,我们采用的是迭代算法——碟形操作。我们采用数学归纳法来进行说明,具体过程如下:
(1)当 N = 2 2 N=2^2 N=22时,则多项式系数为 x ( 0 ) , x ( 1 ) , x ( 2 ) , x ( 3 ) x(0),x(1),x(2),x(3) x(0),x(1),x(2),x(3),同时 m = 0 , 1 , 2 , 3 m=0,1,2,3 m=0,1,2,3。NTT可以写为下面的形式:
X ( m ) ≡ ∑ n = 0 3 x ( n ) a m n m o d M , m = 0 , 1 , 2 , 3 X(m)\equiv \sum_{n=0}^{3}x(n)a^{mn} ~~~~~mod~M~~~,~m=0,1,2,3 X(m)≡n=0∑3x(n)amn mod M , m=0,1,2,3
而将 m , n m,n m,n写成二进制表达式为:
m = 2 m 1 + m 0 = ( m 1 , m 0 ) 2 m=2m_1+m_0=(m_1,m_0)_2 m=2m1+m0=(m1,m0)2
n = 2 n 1 + n 0 = ( n 1 , n 0 ) 2 n=2n_1+n_0=(n_1,n_0)_2 n=2n1+n0=(n1,n0)2
所以NTT又可改写如下:
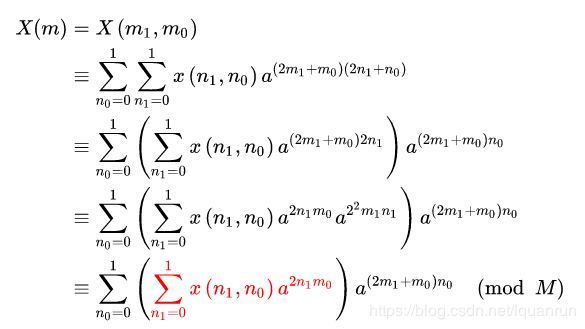
上式成立,因为 a N ≡ 1 ( m o d M ) a^N\equiv 1(mod~M) aN≡1(mod M),且 N = 2 2 N=2^2 N=22,则
a 2 2 m 1 n 1 ≡ 1 ( m o d M ) a^{2^2m_1n_1}\equiv 1(mod~M) a22m1n1≡1(mod M)
然后,令 x ( n 1 , n 0 ) = x 0 ( n 1 , n 0 ) x(n_1,n_0)=x_0(n_1,n_0) x(n1,n0)=x0(n1,n0),且
x 1 ( m 0 , n 0 ) = ∑ n 1 = 0 1 x 0 ( n 1 , n 0 ) a 2 n 1 m 0 = x 0 ( 0 , n 0 ) + x 0 ( 1 , n 0 ) a 2 m 0 ( m o d M ) x_1(m_0,n_0)=\sum_{n_1=0}^{1}x_0(n_1,n_0)a^{2n_1m_0}=x_0(0,n_0)+x_0(1,n_0)a^{2m_0}~~~~(mod ~M) x1(m0,n0)=n1=0∑1x0(n1,n0)a2n1m0=x0(0,n0)+x0(1,n0)a2m0 (mod M)
则,遍历所有 m 0 , n 0 m_0,n_0 m0,n0的值,我们可得到:
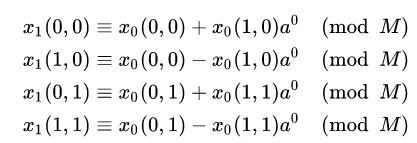
相应的蝶形操作如为:
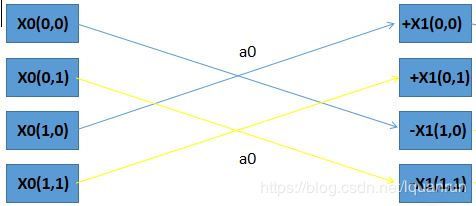
将 x 1 ( m 0 , n 0 ) x_1(m_0,n_0) x1(m0,n0)代入到原式中有:
x 2 ( m 0 , m 1 ) = ∑ n 0 = 0 1 x 1 ( m 0 , n 0 ) a ( 2 m 1 + m 0 ) n 0 = x 1 ( m 0 , 0 ) + x 1 ( m 0 , 1 ) a 2 m 1 + m 0 ( m o d M ) x_2(m_0,m_1)=\sum_{n_0=0}^{1}x_1(m_0,n_0)a^{(2m_1+m_0)n_0}=x_1(m_0,0)+x_1(m_0,1)a^{2m_1+m_0}~~~~(mod ~M) x2(m0,m1)=n0=0∑1x1(m0,n0)a(2m1+m0)n0=x1(m0,0)+x1(m0,1)a2m1+m0 (mod M)
进一步有:
X ( m 1 , m 0 ) = x 2 ( m 0 , m 1 ) ( m o d M ) X(m_1,m_0)=x_2(m_0,m_1)~~~~(mod ~M) X(m1,m0)=x2(m0,m1) (mod M)
相应的蝶形操作如下图:
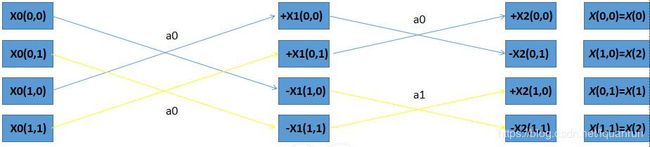
(2)当 N = 2 3 N=2^3 N=23时,同理可得:
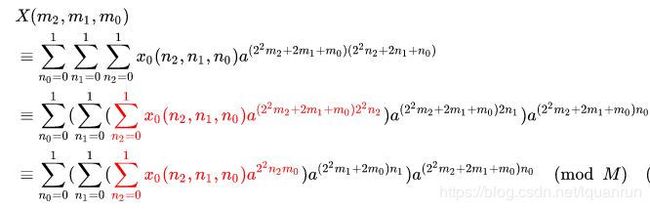
将红色部分提取出来有:
x 1 ( m 0 , n 1 , n 0 ) = x 0 ( 0 , n 1 , n 0 ) + x 0 ( 1 , n 1 , n 0 ) a 4 m 0 ( m o d M ) x_1(m_0,n_1,n_0)=x_0(0,n_1,n_0)+x_0(1,n_1,n_0)a^{4m_0}~~~~(mod ~M) x1(m0,n1,n0)=x0(0,n1,n0)+x0(1,n1,n0)a4m0 (mod M)
遍历 m 0 , n 1 , n 0 m_0,n_1,n_0 m0,n1,n0的值,我们可以得到下图的蝶形操作图:
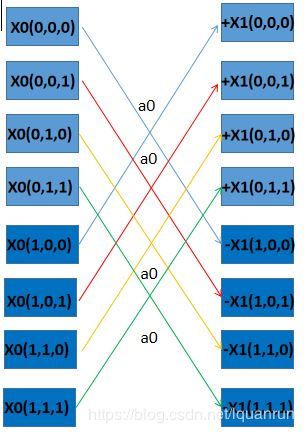
将 x 1 ( m 0 , n 1 , n 0 ) x_1(m_0,n_1,n_0) x1(m0,n1,n0)代入到原式可得:
X ( m 2 , m 1 , m 0 ) = ∑ n 0 = 0 1 ( ∑ n 1 = 0 1 x 1 ( m 0 , n 1 , n 0 ) a ( 2 2 m 1 + m 0 ) n 1 ) a ( 2 2 m 2 + 2 m 1 + m 0 ) n 0 ( m o d M ) X(m_2,m_1,m_0)=\sum_{n_0=0}^{1}(\sum_{n_1=0}^{1}x_1(m_0,n_1,n_0)a^{(2^2m_1+m_0)n_1})a^{(2^2m_2+2m_1+m_0)n_0}~~~~(mod ~M) X(m2,m1,m0)=n0=0∑1(n1=0∑1x1(m0,n1,n0)a(22m1+m0)n1)a(22m2+2m1+m0)n0 (mod M)
将括号内的式子提取出来,并令:
x 2 ( m 0 , m 1 , n 0 ) = ∑ n 1 = 0 1 x 1 ( m 0 , n 1 , n 0 ) a ( 2 2 m 1 + m 0 ) n 1 = x 1 ( m 0 , 0 , n 0 ) + x 1 ( m 0 , 1 , n 0 ) a 4 m 1 + 2 m 0 ( m o d M ) x_2(m_0,m_1,n_0)=\sum_{n_1=0}^{1}x_1(m_0,n_1,n_0)a^{(2^2m_1+m_0)n_1}=x_1(m_0,0,n_0)+x_1(m_0,1,n_0)a^{4m_1+2m_0}~~~~(mod ~M) x2(m0,m1,n0)=n1=0∑1x1(m0,n1,n0)a(22m1+m0)n1=x1(m0,0,n0)+x1(m0,1,n0)a4m1+2m0 (mod M)
遍历 m 0 , m 1 , n 0 m_0,m_1,n_0 m0,m1,n0的值,我们可以得到下图的蝶形操作图:
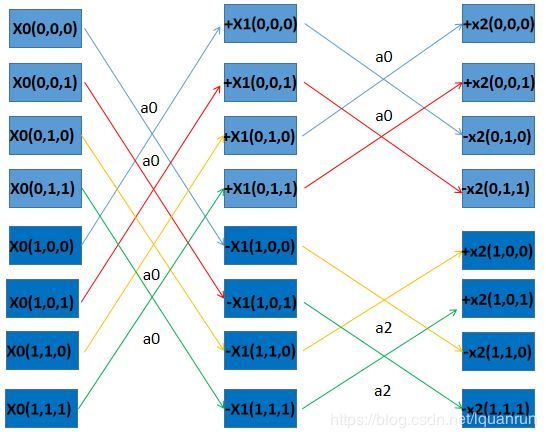
再将 x 2 ( m 0 , m 1 , n 0 ) x_2(m_0,m_1,n_0) x2(m0,m1,n0)代回到原式,我们可以得到:
x 3 ( m 0 , m 1 , m 2 ) = ∑ n 0 = 0 1 x 2 ( m 0 , m 1 , n 0 ) a ( 2 2 m 2 + 2 m 1 + m 0 ) n 0 = x 2 ( m 0 , m 1 , 0 ) + x 2 ( m 0 , m 1 , 1 ) a 4 m 2 + 2 m 1 + m 0 ( m o d M ) x_3(m_0,m_1,m_2)=\sum_{n_0=0}^{1}x_2(m_0,m_1,n_0)a^{(2^2m_2+2m_1+m_0)n_0}=x_2(m_0,m_1,0)+x_2(m_0,m_1,1)a^{4m_2+2m_1+m_0}~~~~(mod ~M) x3(m0,m1,m2)=n0=0∑1x2(m0,m1,n0)a(22m2+2m1+m0)n0=x2(m0,m1,0)+x2(m0,m1,1)a4m2+2m1+m0 (mod M)
同样遍历 m 0 , m 1 , m 2 m_0,m_1,m_2 m0,m1,m2的值,我们可以得到下图的蝶形操作图:
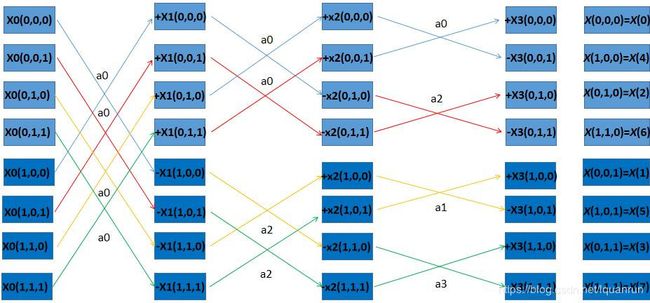
(3)根据数学归纳法,我们可以得到 N = 2 l N=2^l N=2l的情况:
NTT中的正整数序列 m , n m,n m,n可以写为二进制形式:
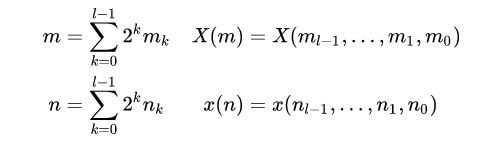

则 a m n a^{mn} amn可以计算为:

进而NTT可以写为下面的形式:
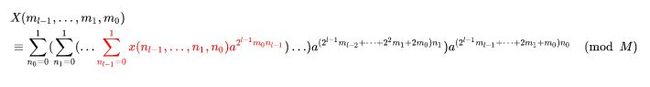
利用(1)、(2)中的思想,将红色内容提取出来有:
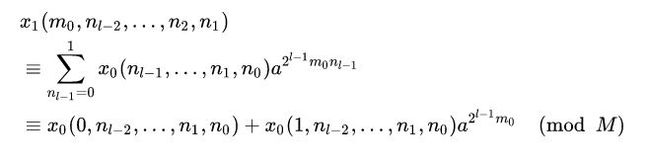
根据数学归纳法,我们可以得到 x r ( m 0 , … , m r − 1 , n l − r − 1 , … , n 0 ) x_r(m_0,\ldots ,m_{r-1},n_{l-r-1},\ldots,n_0) xr(m0,…,mr−1,nl−r−1,…,n0)的一般递推式:
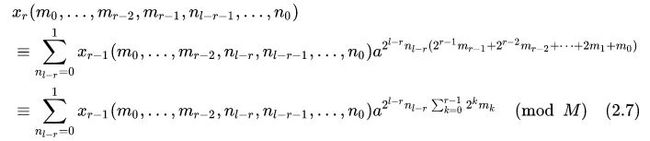
最后,就可以得到:
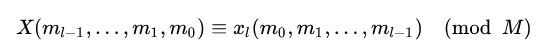
上面内容就是NTT的一般化流程,而每一次红色部分内容的提出本质上就是蝶形操作的一轮。下面就以 r r r轮为例,详细说明蝶形操作的具体流程,即上面的公式(2.7)。在上面的公式中,我们可以容易地发现 x r x_r xr和 x r − 1 x_{r-1} xr−1中除了 n l − r n_{l-r} nl−r不同外,其他部分都一样,故为了方面描述,我们可以简写为:

公式(2.7)可以写为:
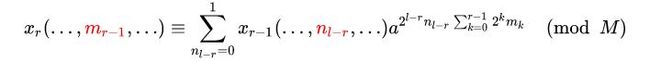
因为 m r − 1 m_{r-1} mr−1和 n l − r n_{l-r} nl−r的取值为0和1,故对应的蝶形操作为:
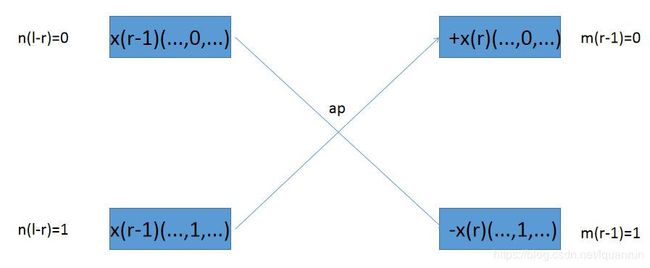
其中,关于 p p p有下面的结论:

证明过程如下,已知 a 2 l − 1 = − a 0 a^{2^{l-1}}=-a^0 a2l−1=−a0:
[1]当 r = 1 r=1 r=1时
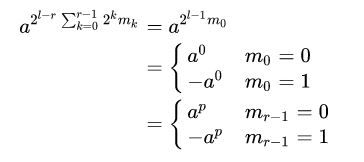
[2]当 r > 1 r>1 r>1时
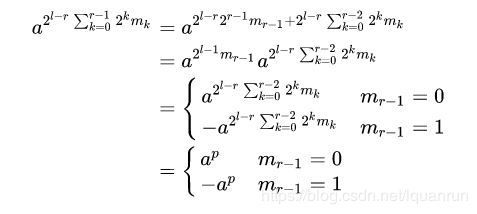
注意:以上部分就是NTT具体数学推导流程,而INTT的思想与NTT完全一致,除了需要在最后的结果上乘上 1 N = 1 2 l \frac{1}{N}=\frac{1}{2^{l}} N1=2l1。而关于NTT在实现方面是有许多改进和注意的地方,这是后续的工作内容,这里就先不叙述了。