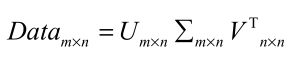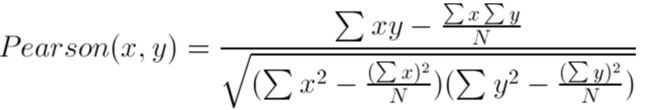机器学习实战-13-利用SVD简化数据

一、SVD介绍

在实际生活中，采集到的数据大部分信息都是无用的噪声和冗余信息，为了剔除掉这些噪声和无用的信息，只保留包含绝大部分重要信息的数据特征，除了上次降到的PCA方法，还有另外一种方法，即SVD（Singular Value Decomposition）。

SVD可以用于简化数据，提取出数据的重要特征，而剔除掉数据中的噪声和冗余信息，能够用小得多的数据集来表示原始数据集。

SVD在现实中可以应用于隐性语义索引（LSI/LSA）、推荐系统用于提升性能，也可以用于图像压缩，节省内存等。

二、SVD原理-矩阵分解

矩阵分解将原始的数据集矩阵data(m*n)分解成三个矩阵U 、 Σ 和 V^T ，他们分别是m行m列、m行n列和n行n列。

对于Sigma矩阵Σ:

• 该矩阵只用对角元素，其他元素均为零
• 对角元素从大到小排列。这些对角元素称为奇异值，它们对应了原始数据集矩阵的奇异值
• 这里的奇异值就是矩阵data特征值的平方根。
• 在某个奇异值的数目（ 1个 ）之后，其他的奇异值都置为0。这就意味着数据集中仅有r个重要特征，而其余特征则都是噪声或冗余特征。

三、利用python实现SVD

全文代码：

from numpy import *
from numpy import linalg as la
import time


def load_ex_data():
    """
    Function:
        创建简单数据集
    Parameters:
        无
    Returns:
        数据集
    Modify:
        2019-1-12
    """
    return [[1, 1, 1, 0, 0],
            [2, 2, 2, 0, 0],
            [1, 1, 1, 0, 0],
            [5, 5, 5, 0, 0],
            [1, 1, 0, 2, 2],
            [0, 0, 0, 3, 3],
            [0, 0, 0, 1, 1]]


def euclids_sim(in_a, in_b):
    """
    Function:
        欧式距离相似度计算
    Parameters:
        in_a - 列向量
        in_b - 列向量
    Returns:
        相似度
    Modify:
        2019-1-12
    """
    return 1.0 / (1.0 + la.norm((in_a - in_b)))


def pears_sim(in_a, in_b):
    """
    Function:
        皮尔逊相关系数相似度计算
    Parameters:
        in_a - 列向量
        in_b - 列向量
    Returns:
        相似度
    Modify:
        2019-1-12
    """
    if len(in_a) < 3:
        return 1.0
    return 0.5 + 0.5 * corrcoef(in_a, in_b, rowvar=0)[0][1]


def cos_sim(in_a, in_b):
    """
    Function:
        余弦距离相似度计算
    Parameters:
        in_a - 列向量
        in_b - 列向量
    Returns:
        相似度
    Modify:
        2019-1-12
    """
    num = float(in_a.T * in_b)
    denom = la.norm(in_a) * la.norm(in_b)
    return 0.5 + 0.5 * (num / denom)


def stand_est(data_mat, user, sim_meas, item):
    """
    Function:
        用户对物品的估计评分值
    Parameters:
        data_mat - 数据矩阵
        user - 用户编号
        sim_meas - 相似度计算方法
        item - 物品编号
    Returns:
        估计评分值
    Modify:
        2019-1-13
    """
    n = shape(data_mat)[1]
    sim_total = 0.0
    rat_sim_total = 0.0
    # 遍历行中的每个物品（对用户评过分的物品进行遍历，并将它与其他物品进行比较）
    for i in range(n):
        user_rating = data_mat[user, i]
        # 如果某个物品的评分值为0，则跳过这个物品
        if user_rating == 0:
            continue
        # 寻找两个用户都评级的物品，获得相比较的两列同时都不为0的数据行号over_lap = [1 2]
        over_lap = nonzero(logical_and(data_mat[:, item].A > 0, data_mat[:, i].A))[0]
        # 如果相似度为0，没有两列同时都不为0的数据行，终止本次循环
        if len(over_lap) == 0:
            similarity = 0
        # 如果存在重合的物品，则基于这些重合物重新计算相似度。
        else:
            similarity = sim_meas(data_mat[over_lap, item], data_mat[over_lap, i])
        # print('the %d and %d similarity is : %f' % (item, i, similarity))
        # 计算总的相似度
        sim_total += similarity
        # 不仅仅使用相似度，而是将评分当权值*相似度 = 贡献度
        rat_sim_total += similarity * user_rating
    # 若该推荐物品与所有列都未比较则评分为0
    if sim_total == 0:
        return 0
    else:
        # 进行归一化，使得最后的评分值在0到5之间
        return rat_sim_total / sim_total


def recommend(data_mat, user, N=3, sim_meas=cos_sim, est_method=stand_est):
    """
    Function:
         推荐引擎，产生评分最高的N个推荐结果
    Parameters:
        data_mat - 数据矩阵
        user - 用户编号
         N - 推荐结果数目，默认3
        sim_meas - 相似度计算方法
        est_method - 估计方法
    Returns:
        推荐N个结果
    Modify:
        2019-1-13
    """
    # 寻找未评级的物品，对给定的用户建立一个未评分的物品列表
    unrated_items = nonzero(data_mat[user, :].A == 0)[1]
    if len(unrated_items) == 0:
        return 'you rated everything'
    items_scores = []
    # 在未评分物品上进行循环
    for item in unrated_items:
        estimated_score = est_method(data_mat, user, sim_meas, item)
        items_scores.append((item, estimated_score))
    return sorted(items_scores, key=lambda jj: jj[1], reverse=True)[:N]


def load_ex_data_2():
    return [[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 5],
            [0, 0, 0, 3, 0, 4, 0, 0, 0, 0, 3],
            [0, 0, 0, 0, 4, 0, 0, 1, 0, 4, 0],
            [3, 3, 4, 0, 0, 0, 0, 2, 2, 0, 0],
            [5, 4, 5, 0, 0, 0, 0, 5, 5, 0, 0],
            [0, 0, 0, 0, 5, 0, 1, 0, 0, 5, 0],
            [4, 3, 4, 0, 0, 0, 0, 5, 5, 0, 1],
            [0, 0, 0, 4, 0, 4, 0, 0, 0, 0, 4],
            [0, 0, 0, 2, 0, 2, 5, 0, 0, 1, 2],
            [0, 0, 0, 0, 5, 0, 0, 0, 0, 4, 0],
            [1, 0, 0, 0, 0, 0, 0, 1, 2, 0, 0]]


def svd_est(data_mat, user, sim_meas, item):
    """
    Function:
        用户对物品的估计评分值
    Parameters:
        data_mat - 数据矩阵
        user - 用户编号
        sim_meas - 相似度计算方法
        item - 物品编号
    Returns:
        估计评分值
    Modify:
        2019-1-14
    """
    n = shape(data_mat)[1]
    sim_total = 0.0
    rat_sim_total = 0.0
    U, Sigma, VT = la.svd(data_mat)
    Sig4 = mat(eye(4) * Sigma[:4])
    xformed_items = data_mat.T * U[:, :4] * Sig4.I
    # 遍历行中的每个物品（对用户评过分的物品进行遍历，并将它与其他物品进行比较）
    for i in range(n):
        user_rating = data_mat[user, i]
        # 如果某个物品的评分值为0，则跳过这个物品
        if user_rating == 0 or i == item:
            continue
        similarity = sim_meas(xformed_items[item, :].T, xformed_items[i, :].T)
        # print('the %d and %d similarity is : %f' % (item, i, similarity))
        # 计算总的相似度
        sim_total += similarity
        # 不仅仅使用相似度，而是将评分当权值*相似度 = 贡献度
        rat_sim_total += similarity * user_rating
    # 若该推荐物品与所有列都未比较则评分为0
    if sim_total == 0:
        return 0
    else:
        # 进行归一化，使得最后的评分值在0到5之间
        return rat_sim_total / sim_total


def print_mat(in_mat, thresh=0.8):
    """
    Function:
        打印矩阵
    Parameters:
        in_mat - 数据矩阵
        thresh - 阈值
    Returns:
        无
    Modify:
        2019-1-19
    """
    for i in range(32):
        for k in range(32):
            if float(in_mat[i, k]) > thresh:
                print(1, end='')
            else:
                print(0, end='')
        print('')


def img_compress(num_sv=3, thresh=0.8):
    """
    Function:
        压缩图像，基于任意给定的奇异值数目重构图像
    Parameters:
        num_sv - 奇异值数目
        thresh - 阈值
    Returns:
        无
    Modify:
        2019-1-19
    """
    myl = []
    # 打开文本文件，以数值方式读入字符
    for line in open('./machinelearninginaction/Ch14/0_5.txt').readlines():
        new_row = []
        for i in range(32):
            new_row.append(int(line[i]))
        myl.append(new_row)
    my_mat = mat(myl)
    print('****original matrix****')
    print_mat(my_mat, thresh)
    # 对原始图像进行SVD分解
    U, Sigma, VT = la.svd(my_mat)
    # 初始化新对角矩阵
    sig_recon = mat(zeros((num_sv, num_sv)))
    # 构造对角矩阵，将特征值填充到对角线
    for k in range(num_sv):
        sig_recon[k, k] = Sigma[k]
    # 通过截断的U和VT矩阵，用sig_recon得到重构后的矩阵
    recon_mat = U[:, :num_sv] * sig_recon * VT[:num_sv, :]
    print('****reconstructed matrix using %d singular values******' % (num_sv))
    print_mat(recon_mat, thresh)


if __name__ == '__main__':
    # U, Sigma, VT = linalg.svd([[1, 1], [7, 7]])
    # print('U:', U)
    # print('Sigma:', Sigma)
    # print('VT:', VT)
    #
    # data = load_ex_data()
    # print('data', data)
    # U, Sigma, VT = linalg.svd(data)
    # print(Sigma)
    #
    # Sig3 = mat([[Sigma[0], 0, 0],
    #     [0, Sigma[1], 0],
    #     [0, 0, Sigma[2]]])
    #
    # restructure_data = U[:, :3] * Sig3 * VT[:3, :]
    # print('origin_mat:', restructure_data)
    #
    # my_data = mat(load_ex_data())
    # euclids = euclids_sim(my_data[:, 0], my_data[:, 4])
    # pears = pears_sim(my_data[:, 0], my_data[:, 4])
    # cos = cos_sim(my_data[:, 0], my_data[:, 4])
    # print('euclids:', euclids)
    # print('pears:', pears)
    # print('cos:', cos)
    #
    # my_data = mat(
    # [[4, 4, 0, 2, 2],
    # [4, 0, 0, 3, 3],
    # [4, 0, 0, 1, 1],
    # [1, 1, 1, 2, 0],
    # [2, 2, 2, 0, 0],
    # [5, 5, 5, 0, 0],
    # [1, 1, 1, 0, 0]]
    # )
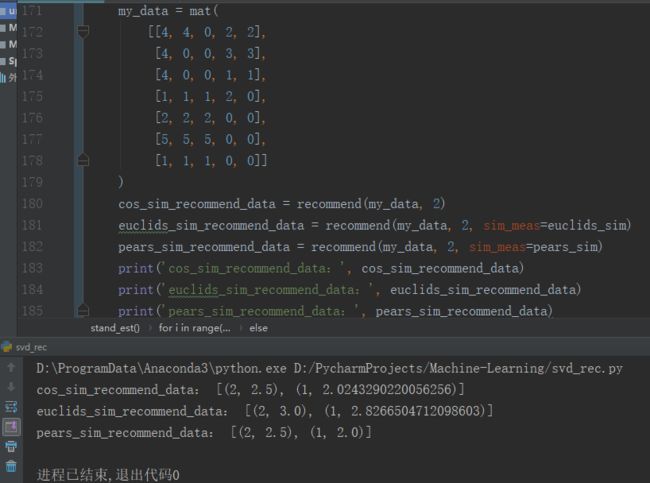
    # cos_sim_recommend_data = recommend(my_data, 2)
    # euclids_sim_recommend_data = recommend(my_data, 2, sim_meas=euclids_sim)
    # pears_sim_recommend_data = recommend(my_data, 2, sim_meas=pears_sim)
    # print('cos_sim_recommend_data：', cos_sim_recommend_data)
    # print('euclids_sim_recommend_data：', euclids_sim_recommend_data)
    # print('pears_sim_recommend_data：', pears_sim_recommend_data)
    #
    # my_data = mat(load_ex_data_2())
    # U, Sigma, VT = linalg.svd(my_data)
    # print('Sigma:', Sigma)
    # Sig2 = Sigma ** 2
    # print('sum(Sig2):', sum(Sig2))
    # print('sum(Sig2) * 0.9:', sum(Sig2) * 0.9)
    # print('sum(Sig2[:2]):', sum(Sig2[:2]))
    # print('sum(Sig2[:3]):', sum(Sig2[:3]))
    #
    # svd_start_time = time.time()
    # svd_my_data = mat(load_ex_data_2())
    # svd_recommond = recommend(svd_my_data, 1, est_method=svd_est)
    # svd_end_time = time.time()
    # print('svd_recommond', svd_recommond)
    # print('svd_recommond共花费时间', svd_end_time - svd_start_time)
    #
    # start_time = time.time()
    # my_data = mat(load_ex_data_2())
    # recommond = recommend(my_data, 1, est_method=stand_est)
    # end_time = time.time()
    # print('svd_recommond', recommond)
    # print('recommond共花费时间', end_time - start_time)

    img_compress(2)

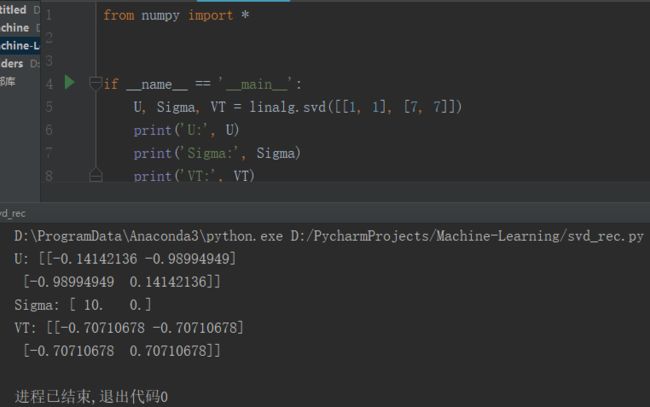
Numpy中称为linalg的线性代数工具箱：la.svd()

注意到矩阵 Sigma 以行向量 array([ 10., 0.]) 返回，而非如下矩阵：

由于矩阵除了对角元素其他均为 0 ，因此这种仅返回对角元素的方式能够节省空间，这就是由 NumPy 的内部机制产生的，一旦看到 Sigma 就要知道它是一个矩阵。

由上图可以看到，Sigma是以数组的形式呈现的，此外，前三个数值比其他值大很多个数量级。于是以将最后两个值去掉，只保留下前三个值，这样，SVD公式就变成这样：Dm×n=Um×3 Σ3×3和VT3×n。也是只用矩阵U的前三列和VT的前三行进行计算从而将原始数据转化到低维度的空间。

确定要保留的奇异值的数目r有很多启发式的策略，其中一个典型的做法就是保留矩阵中 90% 的能量信息。为了计算总能量信息，将所有的奇异值求其平方和。于是可以将奇异值的平方和累加到总值的 90% 为止。另一个启发式策略就是，当矩阵上有上万的奇异值时，那么就保留前面的 2000 或 3000 个。

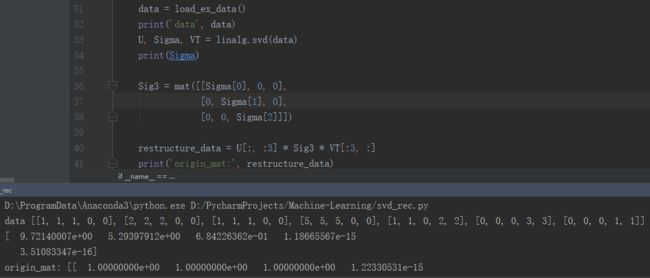
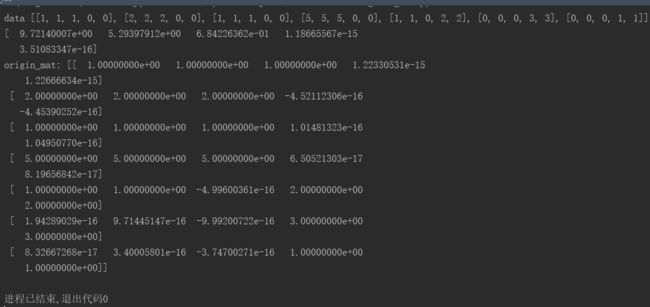
现在根据以上试图重构原始矩阵。

四、基于协同过滤的推荐引擎

推荐引擎是机器学习的一个重要应用，比如Amazon会根据顾客的购买历史向他们推荐物品，Netflix会像其用户推荐电影，新闻网站会对用户推荐新闻报道等等。当然，有很多方法可以实现推荐功能，比如基于内容的推荐，是通过机器学习的方法，比如决策树，神经网络等从用户对于物品的评价的内容特征描述中得到用户感兴趣的资料，而不需要其他用户的数据。而基于协同过滤的推荐方法则是通过将用户与其他用户的数据进行比对，依据相似度的大小实现推荐。

在进行协同过滤之前，我们需要将数据转化为合理的形式，即将数据转化为矩阵的形式，这样，便于我们处理和计算相似度。当我们计算出了用户或者物品之间的相似度，我们就可以利用已有的数据来预测未知的用户喜好。比如，我们试图对某个用户喜欢的电影进行预测，推荐引擎会发现有一部电影该用户没有看过。然后，就会计算该电影和用户看过电影之间的相似度，如果相似度很高，推荐算法就会认为用户喜欢这部电影。

4.1 相似度计算

• 1. 欧式距离（0~1）：
     相似度 = 1/ (1 + 距离)
• 2. 皮尔逊相关系数(Pearson correlation):

该方法相对于欧氏距离的一个优势在于，它对用户评级的量级并不敏感。比如某个狂躁者对所有物品的评分都是5分 ，而另一个忧郁者对所有物品的评分都是1分，皮尔逊相关系数会认为这两个向量是相等的。

皮尔逊相关系数的计算是由Numpy中的corrcoef()函数，他的取值范围在：(-1~1)，皮尔逊相关系数的取值范围从-1到+1，我们通过0.5 + 0 . 5 * corrcoef()把其取值范围归一化到0到 1之间。

• 3. 余弦相似度（cosine similarity）

其中，在Numpy中计算范数的公式：linalg.norm()

上面的相似度计算都是假设数据采用了列向量方式进行表示。如果利用上述函数来计算两个行向量的相似度就会遇到问题（我们很容易对上述函数进行修改以计算行向量之间的相似度)。这里采用列向量的表示方法，暗示着我们将利用基于物品的相似度计算方法。

4.2 基于物品的相似度还是基于用户的相似度？

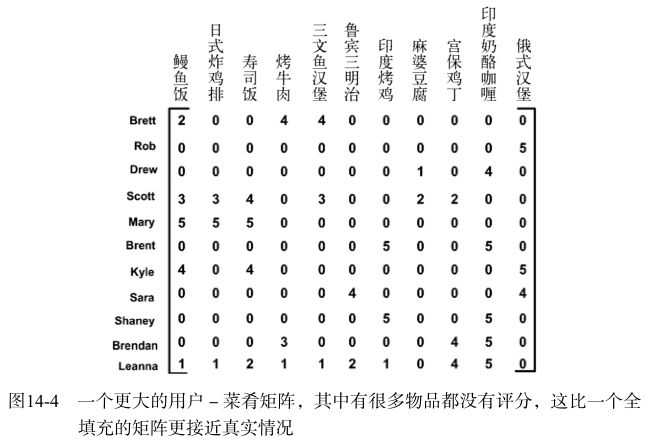
4.1计算了两个餐馆菜肴之间的距离，这称为基于物品（item-based）的相似度。另一种计算用户距离的方法则称为基于用户（user-based）的相似度。上图 ，行与行之间比较的是基于用户的相似度，列与列之间比较的则是基于物品的相似度。

到底使用哪一种相似度呢？这取决于用户或物品的数目。基于物品相似度计算的时间会随物品数量的增加而增加，基于用户的相似度计算的时间则会随用户数量的增加而增加。对于大部分产品导向的推荐引擎而言，用户的数量往往大于物品的数量，即购买商品的用户数会多于出售的商品种类。

4.3 推荐引擎的评价

采用交叉测试的方法。具体的做法就是，我们将某些已知的评分值去掉，然后对它们进行预测，最后计算预测值和真实值之间的差异。

评价的指标是称为最小均方根误差（ RootMeanSquaredError, RMSE ) 的指标。它首先计算均方误差的平均值然后取其平方根。如果评级在1星到5星这个范围内，而我们得到的为1.0,那么就意味着我们的预测值和用户给出的真实评价相差了一个星级。

五、示例：餐馆菜肴推荐引擎

构建一个基本的推荐引擎，它能够寻找用户没有尝过的菜肴。然后，通过 SVD 来减少特征空间并提高推荐的效果。这之后，将程序打包并通过用户可读的人机界面提供给人们使用。

5.1推荐未尝过的菜肴

(1) 寻找用户没有评级的菜肴，即在用户－物品矩阵中的 0 值；
(2) 在用户没有评级的所有物品中，对每个物品预计一个可能的评级分数。也就是我们认为用户可能会对物品的打分（这就是相似度计算的初衷）；
(3) 对这些物品的评分从高到低进行排序，返回前N个物品。

基于物品3种相似度计算推荐结果

5.2 利用SVD提高推荐的效果

实际的数据集会比我们用于展示 recommend() 函数功能的 myMat 矩阵稀疏得多。图14-4就给出了一个更真实的矩阵的例子。

利用上述数据集计算该矩阵的SVD了解其到底需要多少维特征。

首先，对Sigma中的值求平方，再计算总能量和总能量的90%。 然后计算前两个元素所包含的能量，该值低于总能量的 90% ，于是计算前三个元素所包含的能量，该值高于总能量的 90% ，这就可以确定需要3维特征。于是，可以将一个11维的矩阵转换成一个3维的矩阵。

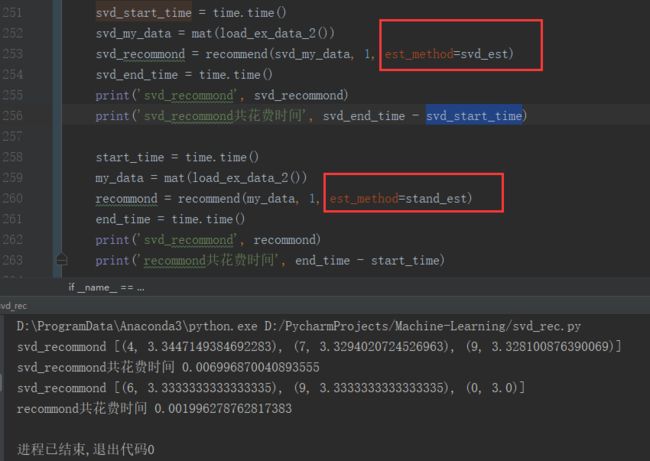
下面对转换后的三维空间构造出一个相似度计算函数。利用SVD将所有的菜肴映射到一个低维空间中去。在低维空间下，可以利用前面相同的相似度计算方法来进行推荐。

从上图花费时间上看，做了SVD分解的推荐计算效率稍稍慢一点。

5.3 构建推荐引擎面临的挑战

• 我们不必在每次评分是都做SVD分解，大规模数据上可能降低效率，可以在程序调用时运行一次，在大型系统中每天运行一次或频率不高，还要离线运行；
• 矩阵中有很多0，实际系统中0更多，可以通过只存储非0元素来节省空间和计算开销；
• 计算资源浪费来自于相似度的计算，每次一个推荐时都需要计算多个物品评分（即相似度），在需要时此记录可以被用户重复使用。实际中，一个普遍的做法是离线计算并保存相似度得分。
• 推荐引擎面临的另一个问题就是如何在缺乏数据时给出好的推荐。

5.4 基于SVD的图像压缩

手写识别数字的图像在第KNN那篇使用过，原始的图像大小是 32×32=1024 像素，我们能基于SVD的图像压缩使用更少的像素来表示这张图，这样就可以节省空间或带宽开销了。

可知，只需两个奇异值就能相当精确地对图像实现重构。U和VT都是32x2的矩阵，加上两个奇异值。因此，需要总数字数目是64+64+2=130个0-1的数字来就可以重构图像了。和原数目1024相比，获得了几乎10倍的压缩比。

SVD两个最重要的计算步骤这：
数据集降维：这里的Sigma为对角矩阵（需要利用原来svd返的Sigma向量构建矩阵，构建需要使用count这个值）。U为svd返回的左奇异矩阵，count为我们指定的多少个奇异值，这也是Sigma矩阵的维数。

重构数据集：这里的Sigma同样为对角矩阵（需要利用原来svd返回的Sigma向量构建矩阵，构建需要使用count这个值），VT为svd返回的右奇异矩阵，count为我们指定的多少个奇异值（可以按能量90%规则选取）。

六、小结

SVD是一种强大的降维工具，可以利用SVD来逼近矩阵并从中提取重要特征。通过保留80%-90%的能量，就可以得到重要的特征并去掉噪声。

推荐引擎将物品推荐给用户，协同过滤是一种基于用户喜好或行为数据的推荐的实现方法。协同过滤的核心是相似度计算方法，有很多相似度计算方法都可以用于计算物品或用户之间的相似度。通过在低维空间下计算相似度，SVD提高了推荐引擎的效果。

在大规模数据集上，SVD的计算和推荐可能是一个很困难的工程问题。通过离线方式来进行SVD分解和相似度计算，是一种减少冗余计算和推荐所需时间的方法。