最小生成树之Prim和Kruskal代码详解

Prim

原理：选一个顶点加入U找出这个顶点权值最小边，得到新顶点加入U，然后继续找出U中的顶点 连接其他顶点的最小边，直到全部顶点进入U中

适用稠密结构

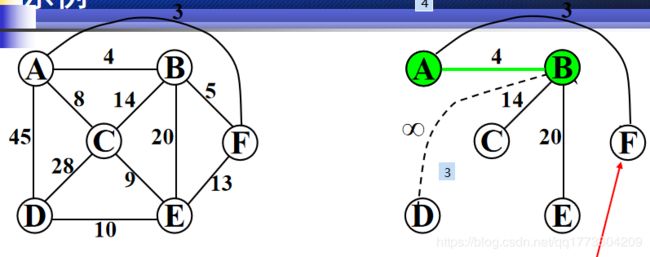
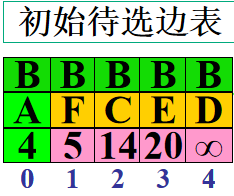
思路：
1. 选择初始顶点，设置到U中（lowcost[v] = 0;）
2. 找出当前U中权值最小边的下标，并把当前顶点添加到U中 U{A}
3. 修改数组lowcost和closest，当第二步的新入顶点到相邻顶点比U中其他的顶点更小 如上图A->F比B->F权值更小，直接替换
4. 重复2，3步

#include 
#include 
#include 
using namespace std;

typedef char VertexType;             //顶点类型应由用户定义
typedef int EdgeType;              //边上的权值类型应由用户定义

#define MAXVEX  10             //最大顶点数，应由用户定义
#define MaxSize 20             //最大边数，应由用户定义
#define INF 32767		//INF表示∞

struct MatMatGraph {
    VertexType vexs[MAXVEX];            //顶点表
    EdgeType   edges[MAXVEX][MAXVEX];   //邻接矩阵，可看作边
    int numVertexes, numEdges;      //图中当前的顶点数和边数
};

//定位
int locates(MatMatGraph* g, char ch) {
    int i = 0;
    for (i = 0; i < g->numVertexes; i++) {
        if (g->vexs[i] == ch) {
            break;
        }
    }
    if (i >= g->numVertexes) {
        return -1;
    }
    return i;
}
//建立一个无向网图的邻接矩阵表示
void CreateMatGraph(MatMatGraph* g) {
    int i, j, k, w;
    cout << "输入顶点数和边数:" << endl;
    cin >> g->numVertexes >> g->numEdges;

    cout << "请输入顶点名称，每个顶点用单个字母或单个数字表示，并以回车键结束：" << endl;
    for (i = 0; i < g->numVertexes; i++) {
        g->vexs[i] = getchar();
        while (g->vexs[i] == '\n') {
            g->vexs[i] = getchar();
        }
    }
    cout << "你输入的顶点是：";
    for (i = 0; i < g->numVertexes; i++) {
        cout << g->vexs[i];
    }
    cout << endl;
    for (i = 0; i < g->numEdges; i++) {
        for (j = 0; j < g->numEdges; j++) {
            g->edges[i][j] = 0; //邻接矩阵初始化为每个单元为零
        }
    }
    cout << "输入边(vi,vj)上的顶点i名称，顶点j名称和权值,每个项点输入后以回键结束" << endl;
    for (k = 0; k < g->numEdges; k++) {
        char p, q;
        cin >> p >> q;
        cin >> w;
        int m = -1;
        int n = -1;
        // 获取顶点下标
        m = locates(g, p);
        n = locates(g, q);
        if (m == -1 || n == -1) {
            cout << "there is no vertex." << endl; //显示输入有错信息, 顶点不存在
            return;
        }
        g->edges[m][n] = w;
        g->edges[n][m] = w;  //因为是无向图，矩阵对称
    }
}
//打印图
void printMatGraph(MatMatGraph g) {
    int i, j;
    cout << "这个邻接矩阵为：" << endl;
    for (i = 0; i < g.numVertexes; i++) {
        for (j = 0; j < g.numVertexes; j++) {
            cout << setw(10) << g.edges[i][j];
        }
        cout << endl;
    }
}

/*Prim*/
/*
    思路：
    1. 选择初始顶点，设置到U中（lowcost[v] = 0;）
    2. 找出当前U中权值最小边的下标，并把当前顶点添加到U中   U{A}
    3. 修改数组lowcost和closest，当第二步的新入顶点到相邻顶点比U中其他的顶点更小，则替换出来  U{A,C} 如果lowcost数组中 A->B:权值20 替换为 C->B:权值10
    4. 重复2，3步
*/
void Prim(MatMatGraph g, int v)
{
    int lowcost[MAXVEX]; //存放当前顶点所连接的边
    int min;
    int closest[MAXVEX], i, j, k;
    for (i = 0; i < g.numVertexes; i++)	//给lowcost[]和closest[]置初值
    {
        if (i != v)
        {
            if (g.edges[v][i] == 0)
                lowcost[i] = INF;
            else
                lowcost[i] = g.edges[v][i]; // 第一个顶点中每条边的权重
        }
        else
            lowcost[i] = 0;     //标记k已经加入U
        closest[i] = v;
    }
    k = 0;
    for (i = 1; i < g.numVertexes; i++)	  	//输出(n-1)条边
    {
        min = INF;
        for (j = 0; j < g.numVertexes; j++) 	//在(V-U)中找出离U最近的顶点k
            if (lowcost[j] != 0 && lowcost[j] < min)
            {
                min = lowcost[j];
                k = j;			//k记录最近顶点编号
            }
        printf(" 边(%d，%d)权为:%d\n", closest[k], k, min);
        lowcost[k] = 0;		//标记k已经加入U
        for (j = 0; j < g.numVertexes; j++)  //修改数组lowcost和closest 当前k顶点所连接边中 权值小的 替换 当前表中 权值大的边
            if (lowcost[j] !=0 && g.edges[k][j] < lowcost[j] && g.edges[k][j] !=0)
            {
                lowcost[j] = g.edges[k][j];
                closest[j] = k;
            }
    }
}


int main()
{
    MatMatGraph g;
    CreateMatGraph(&g); //邻接矩阵创建图
    printMatGraph(g); //打印邻接矩阵
    Prim(g, 0);

    getchar();
    getchar();
	return 0;
}

Kruskal

原理：找出所有最小边拼出一个最小生成树
适用稀疏结构

思路：

1. 构造边结构体
   typedef struct
   {
   int u; //边的起始顶点
   int v; //边的终止顶点
   int w; //边的权值
   } Edge;
2. 按照权值排序
3. 依次取出结构体数组中的边
4. 通过辅助数组进行编号，防止回路

#include 
#include 
#include 
using namespace std;

typedef char VertexType;             //顶点类型应由用户定义
typedef int EdgeType;              //边上的权值类型应由用户定义

#define MAXVEX  10             //最大顶点数，应由用户定义
#define MaxSize 20             //最大边数，应由用户定义
#define INF 32767		//INF表示∞

struct MatMatGraph {
    VertexType vexs[MAXVEX];            //顶点表
    EdgeType   edges[MAXVEX][MAXVEX];   //邻接矩阵，可看作边
    int numVertexes, numEdges;      //图中当前的顶点数和边数
};

typedef struct
{
    int u;     	//边的起始顶点
    int v;     	//边的终止顶点
    int w;   	//边的权值
} Edge;

//定位
int locates(MatMatGraph* g, char ch) {
    int i = 0;
    for (i = 0; i < g->numVertexes; i++) {
        if (g->vexs[i] == ch) {
            break;
        }
    }
    if (i >= g->numVertexes) {
        return -1;
    }
    return i;
}
//建立一个无向网图的邻接矩阵表示
void CreateMatGraph(MatMatGraph* g) {
    int i, j, k, w;
    cout << "输入顶点数和边数:" << endl;
    cin >> g->numVertexes >> g->numEdges;

    cout << "请输入顶点名称，每个顶点用单个字母或单个数字表示，并以回车键结束：" << endl;
    for (i = 0; i < g->numVertexes; i++) {
        g->vexs[i] = getchar();
        while (g->vexs[i] == '\n') {
            g->vexs[i] = getchar();
        }
    }
    cout << "你输入的顶点是：";
    for (i = 0; i < g->numVertexes; i++) {
        cout << g->vexs[i];
    }
    cout << endl;
    for (i = 0; i < g->numEdges; i++) {
        for (j = 0; j < g->numEdges; j++) {
            g->edges[i][j] = 0; //邻接矩阵初始化为每个单元为零
        }
    }
    cout << "输入边(vi,vj)上的顶点i名称，顶点j名称和权值,每个项点输入后以回键结束" << endl;
    for (k = 0; k < g->numEdges; k++) {
        char p, q;
        cin >> p >> q;
        cin >> w;
        int m = -1;
        int n = -1;
        // 获取顶点下标
        m = locates(g, p);
        n = locates(g, q);
        if (m == -1 || n == -1) {
            cout << "there is no vertex." << endl; //显示输入有错信息, 顶点不存在
            return;
        }
        g->edges[m][n] = w;
        g->edges[n][m] = w;  //因为是无向图，矩阵对称
    }
}
//打印图
void printMatGraph(MatMatGraph g) {
    int i, j;
    cout << "这个邻接矩阵为：" << endl;
    for (i = 0; i < g.numVertexes; i++) {
        for (j = 0; j < g.numVertexes; j++) {
            cout << setw(10) << g.edges[i][j];
        }
        cout << endl;
    }
}

void InsertSort(Edge* arr, int len)//插入排序
{
    Edge  temp;
    int j;
    for (int i = 1; i < len; ++i)//从arr[1]开始一个个插入到前面的内容
    {
        //要插入的元素是arr[i]
        temp = arr[i];
        for (j = i - 1; j >= 0; --j)
        {
            if (arr[j].w < temp.w) break;
            arr[j + 1] = arr[j];//不然把这个元素放到后面的位置(往后移动)
        }
        arr[j + 1] = temp;//插入这个元素
    }
}

void Kruskal(MatMatGraph g)
{
    int i, j, u1, v1, sn1, sn2, k;
    int vset[MAXVEX];
    Edge E[MaxSize];		//存放所有边
    k = 0;				//E数组的下标从0开始计
    for (i = 0; i < g.numVertexes; i++)	//由g产生的边集E
        for (j = 0; j < g.numVertexes; j++)
            if (g.edges[i][j] != 0 && g.edges[i][j] != INF)
            {
                E[k].u = i;  E[k].v = j;  E[k].w = g.edges[i][j];
                k++;
            }

    InsertSort(E, g.numEdges * 2);		//用直接插入排序对E数组按权值递增排序

    for (i = 0; i < g.numVertexes; i++) 	//初始化辅助数组
        vset[i] = i;

    k = 1;				//k表示当前构造生成树的第几条边
    j = 0;				//E中边的下标，初值为0
    while (k < g.numVertexes)		//生成的边数小于numVertexes时循环
    {
        u1 = E[j].u; v1 = E[j].v;	//取一条边的头尾顶点
        sn1 = vset[u1];
        sn2 = vset[v1];		//分别得到两个顶点所属的集合编号
        if (sn1 != sn2)  		//两顶点属于不同的集合
        {
            printf("  (%d，%d):%d\n", u1, v1, E[j].w);
            k++;		   	//生成边数增1
            for (i = 0; i < g.numVertexes; i++)  	//两个集合统一编号，防止出现回路
                if (vset[i] == sn2) 	//集合编号为sn2的改为sn1
                    vset[i] = sn1;
        }
        j++;			//扫描下一条边
    }
}

int main()
{
    MatMatGraph g;
    CreateMatGraph(&g); //邻接矩阵创建图
    printMatGraph(g); //打印邻接矩阵
    Kruskal(g);

    getchar();
    getchar();
    return 0;
}