线段树总结（萌新必看）

线段树

走进线段树

线段树是什么？
顾名思义，就是把一颗树拆成若干个点段，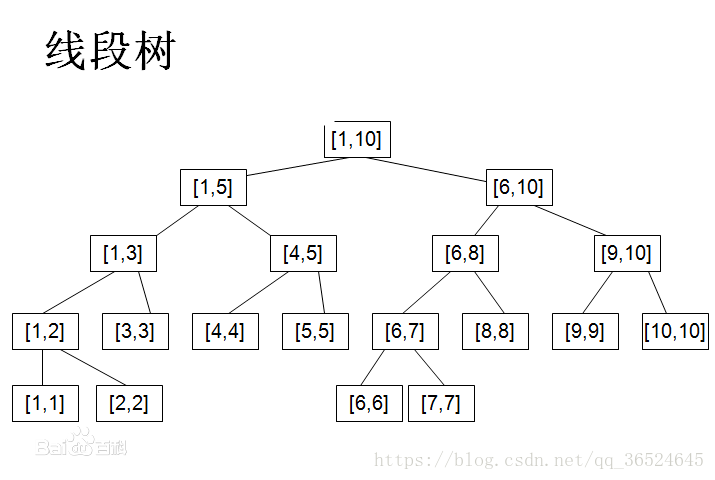
每一个父结点可以包含其子节点的信息（看你要表示什么了），例如该父结点的全部子节点的值之和，该父节点范围内子节点的最大值，那么就可以采取一些例如区间查询，区间修改，单点查询，单点修改的操作了，显然是用空间来换时间的算法（有了父节点就不用一直追溯到字节点，时间效率会提升很多，但是由于开了很多没必要的父节点，空间上比一般算法会多一些），那么既然大致理解了线段树的含义，那么就看一下基本操作了～

算法之前

线段树的根节点由图（挺丑的，看得懂就好..）可以看出是编号为1的节点，这并不是随机，单纯的为了好操作，每一个父节点的左右子树的编号分别为：rt<<1, rt << 1 | 1,其中rt表示的是父节点在结构体里面的编号，要是还不理解的话，这样用动态的思路考虑一下，首先根节点的编号是1，父节点需要向下建树推子节点，两个子节点分别是2（1 << 1），3(1 << 1 | 1)，依次推下去，2的子节点是4（2 << 1），5(2 << 1 | 1)，3的子节点是6(3 << 1)，7(3 << 1 | 1),说白了这一方面是为了建一颗完全二叉树,一方面也是好写（好写吗..）。
来一个建树代码来看一看：

void build(long long rt,long long l,long long r){
	if(l == r){
		tree[rt] = a[l];//到了单个节点，也可以说叶子节点，直接赋值
		return;
	}
	long long mid = (l + r) >> 1;//取中点
	build(rt << 1, l, mid);//递归左子树
	build(rt << 1 | 1, mid + 1, r);//递归右子树
	tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];//这个是区间求和，要是求区间最大值就换成max就好了
}

一般没必要开long long，我纯属闲的（反正不开白不开）。
到了这里大家应该理解了线段树大致是个什么东西了吧，个人认为挺好理解的。

区间修改&区间查询

这里就不单独写单点修改了单点查询了，毕竟没啥用，而且会了区间修改查询之后把l和r换成一样的不就好了吗（偷懒）。
区间修改相信初学者一开始不好理解，我先放代码再解释

区间加法

void update(long long rt, long long l, long long r, long long w){//修改操作
	tree[rt] += (r-l+1)*w;//区间加和，其父亲节点加的一定是其区间内左右子树的加和的总和，即区间的大小乘单个节点要加的值
	lazy[rt] += w;//为了其子节点做准备
}

void pushdown(long long rt,long long l, long long r){//下推lazy标志并修改左右子树的值
	long long mid = (l + r) >> 1;
	update(rt << 1, l, mid, lazy[rt]);//修改左子树
	update(rt << 1 | 1, mid + 1, r, lazy[rt]);//修改右子树
	lazy[rt] = 0;//清空lazy标志
}

void modify(long long rt,long long l,long long r,long long s,long long t,long long w){//s和t是两个变量，用来记录当前到了那个区间，而s和t用来记录要查询的区间
	if(s <= l && t >= r){
		update(rt,l,r,w);//要查找的内容包括了本区间
		return;
	}
	pushdown(rt, l, r);
	long long mid = (l + r) >>1;
	if(s <= mid) modify(rt << 1, l, mid, s, t, w);//mid在左端点的右面且l小于左端点
	if(t > mid) modify(rt << 1 | 1, mid + 1, r, s, t, w);//mid在右端点左面且大于r右端点
	tree[rt] = tree[rt << 1] + tree[rt << 1 | 1];//区间求和
}

那么lazy标记到底是什么呢？要知道一点，线段树修改时并不会直接修改到叶子节点，那样时间效率并不高，也失去了父亲节点存在的意义，当父亲节点的区间在要询问的区间内部的时候，只会修改父节点的值而不会更新子节点的值，也就是说，当子节点需要更新的时候才会采取操作，那么lazy标志就是记录的父节点欠子节点的值，这里可能不太好理解，可以自己模拟一下过程，按照代码模拟一下就懂了（懒了），别人再怎么解释不懂还是不懂，自己实际去模拟一下，多品，细品，就会恍然大悟（雾）。这里具体还是看代码和模拟为主。

区间查询

区间查询相对于区间修改就好理解的多，解释看备注吧，和上面的modify函数一模一样～～

long long query(long long rt, long long l, long long r, long long s, long long t){
	if(s <= l && t >= r){
		return tree[rt];//在要查询的区间里直接返回值
	}
	long long mid = (l + r) >> 1;
	pushdown(rt, l, r);//把lazy标志下推，否则查询出来的信息是错的（毕竟不是所有的数都在一整个区间里，可能跨区间）
	if(t <= mid){
		return query(rt << 1, l, mid, s, t);
	}else if(s > mid){
		return query(rt << 1 | 1, mid + 1, r, s, t);
	}//同区间修改
	else return query(rt << 1, l, mid, s, t) + query(rt << 1 | 1, mid + 1, r, s, t);//此处是区间求和，求区间最大值只要改成max就好了
}

区间乘法

这是个人认为线段树里最恶心的一种操作，即让一个区间全都乘上一个数，一开始想不过如此的操作，看起来和加法没什么区别，但是仔细一想不要忘了一个细节：线段树并不会更新到叶子节点,那么就要考虑一下算法的顺序了，要是加法标记没有推下去而直接算乘法，显然是错解。
这样想，好像并不好操作，那简化一下，运用乘法分配率即\((a+lazy[b])*lazy_[c]=a*lazy_[c]+lazy[b]*lazy_[c]\)，说白了就是先乘后加，再向下推lazy标记的时候就不会出现如上的错解。
上代码：

#include
const int maxn = 1e5+5;

long long tree[maxn << 2],lazy[maxn << 2], lazy_[maxn << 2],x[maxn];//线段树不要忘记要左移两位，数组别开小了
int n,m,order,add,mod;
using namespace std;

void build(int rt, int l, int r){
	lazy_[rt] = 1;
	if(l == r){
		tree[rt] = x[l] % mod;
		return;
	}
	int mid = (l + r) >> 1;
	build(rt << 1, l, mid);
	build(rt << 1 | 1, mid + 1, r);
	tree[rt] = (tree[rt << 1] + tree[rt << 1 | 1])%mod;
}

void update(int rt, int l, int r, long long w, long long cheng){
	lazy_[rt] =(lazy_[rt]*cheng)%mod;
	lazy[rt] = (lazy[rt]*cheng) %mod;//先乘
	lazy[rt] = (lazy[rt]+ w)%mod;//后加
	tree[rt] =( tree[rt] * cheng + (r - l + 1)*w )%mod;
}

void pushdown(int rt, int l, int r){
	int mid = (l + r) >> 1;
	update(rt << 1, l, mid, lazy[rt],lazy_[rt]);
	update(rt << 1 | 1, mid + 1, r, lazy[rt], lazy_[rt]);
	lazy[rt] = 0;
	lazy_[rt] = 1;
}

void modify(int rt, int l, int r, int s, int t, long long w, long long cheng){//通俗易懂，w就是加，cheng就是cheng，此函数就是区间修改
	if(l >= s && r <= t){
		update(rt, l, r, w, cheng);//直接修改
		return;
	}
	pushdown(rt,l,r);//lazy标记下推
	int mid = (l + r) >> 1;
	if(mid >= s) modify(rt << 1, l, mid, s, t, w, cheng);
	if(mid < t) modify(rt << 1 | 1, mid + 1, r, s, t, w, cheng);
	tree[rt] = (tree[rt << 1] + tree[rt << 1 | 1])%mod;
}

long long query(int rt, int l, int r, int s, int t){//区间查询和
	if(l >= s && r <= t){
		return tree[rt]%mod;
	}
	int mid = (l + r) >> 1;
	pushdown(rt, l, r);
	long long ans = 0;
	if(mid >= s) ans = (ans+query(rt << 1, l, mid, s, t)) % mod;
	if(mid < t) ans = (ans + query(rt << 1 | 1, mid + 1, r, s, t)) % mod;
	return ans%mod;
}

void solve(){
	int a,b,add;
	scanf("%d%d%d", &n, &m, &mod);
	for(int i = 1; i <= n; i++) scanf("%lld",&x[i]);
	build(1,1,n);
	for(int i = 1; i <= m; i++){
		scanf("%d",&order);
		if(order == 2){
			scanf("%d%d%d",&a, &b, &add);
			modify(1, 1, n, a, b, add,1);
		}else if(order == 1){
			scanf("%d%d%d", &a, &b, &add);
			modify(1, 1, n, a, b, 0, add);
		}
		else{
			scanf("%d%d", &a, &b);
			printf("%lld\n",query(1,1,n,a,b)%mod);
		}
	}
}
int main(){
	solve();
	return 0;
}

线段树的总结就先写这么多了，以后发现好题还会继续更新～