高数, 大物和概统的梦幻联动? 浅谈Gauss积分和Maxwell-Blotzmann分布的相关计算
0. 事出有因
身为卑微苦逼工科学生, 这个学期要同时学习多元微积分, 概率统计和物理的热力学部分. 然后就遇上了三者的联动: 物理课上出现了身为概率密度函数的Maxwell速率分布函数, 顺便再算一手速率的数学期望以及其平方的数学期望(本质上不是要平方的数学期望, 而是要求所谓的方均根速率, 也就是 v 2 ˉ \displaystyle\sqrt{\bar{v^2}} v2ˉ). 于是乎, 就要算广义积分, 还是没有原函数的那种. 然而, 也因为是卑微的工科学生, 老师并不讲这些东西计算的过程, 而是直接给个公式, 背就完事了. 但是, 我还是想要知其所以然~~, 况且这个不是很困难对吧~~, 于是就有了这篇文章.
0.5 如果你只是想要抄个结果的话
- Gauss积分及其变形
- ∫ − ∞ + ∞ e − α x 2 d x = 2 ∫ 0 + ∞ e − α x 2 d x = π α \displaystyle\int_{-\infty}^{+\infty}e^{-\alpha x^2}\mathop{}\!\mathrm{d}x=2\int_{0}^{+\infty}e^{-\alpha x^2}\mathop{}\!\mathrm{d}x=\sqrt{\frac{\pi}{\alpha}} ∫−∞+∞e−αx2dx=2∫0+∞e−αx2dx=απ
- ∫ − ∞ + ∞ e − a x 2 + b x + c d x = π a e b 2 4 a + c \displaystyle\int_{-\infty}^{+\infty}e^{-ax^2+bx+c}\mathop{}\!\mathrm{d}x=\sqrt{\frac{\pi}{a}}e^{\frac{b^2}{4a}+c} ∫−∞+∞e−ax2+bx+cdx=aπe4ab2+c
- ∫ 0 + ∞ x 2 n + 1 e − α x 2 d x = n ! 2 α n + 1 \displaystyle\int_{0}^{+\infty}x^{2n+1}e^{-\alpha x^2}\mathop{}\!\mathrm{d}x=\frac{n!}{2\alpha^{n+1}} ∫0+∞x2n+1e−αx2dx=2αn+1n!
- ∫ 0 + ∞ x 2 n e − α x 2 d x = ( 2 n − 1 ) ! ! 2 n + 1 α n π α \displaystyle\int_{0}^{+\infty}x^{2n}e^{-\alpha x^2}\mathop{}\!\mathrm{d}x=\frac{(2n-1)!!}{2^{n+1}\alpha^n}\sqrt{\frac{\pi}{\alpha}} ∫0+∞x2ne−αx2dx=2n+1αn(2n−1)!!απ
- Maxwell-Boltzmann分布的常见统计量
- 平均速率 v ˉ = 2 2 k B T π m \displaystyle\bar{v}=2\sqrt{\frac{2k_BT}{\pi m}} vˉ=2πm2kBT
- 方均根速率 v 2 ˉ = 3 k B T m \displaystyle\sqrt{\bar{v^2}}=\sqrt{\frac{3k_BT}{m}} v2ˉ=m3kBT
- 最概然速率 v p = 2 k B T m \displaystyle v_p=\sqrt{\frac{2k_BT}{m}} vp=m2kBT
1. 简单介绍一下
1.1 Gauss积分
我们先来讲讲Gauss(高斯)积分. 狭义的Gauss积分就是Gauss函数 e − x 2 e^{-x^2} e−x2在整个实数域上的广义积分(正态分布内味有了), 即:
∫ − ∞ + ∞ e − x 2 d x \displaystyle\int_{-\infty}^{+\infty}e^{-x^2}\mathop{}\!\mathrm{d}x ∫−∞+∞e−x2dx
顺便一提, 它的结果是 π \sqrt{\pi} π. 而比较广义的Gauss积分则是形如这样的广义积分:
∫ − ∞ + ∞ x n e − a x 2 + b x + c d x \displaystyle\int_{-\infty}^{+\infty}x^ne^{-ax^2+bx+c}\mathop{}\!\mathrm{d}x ∫−∞+∞xne−ax2+bx+cdx
一般而言, n n n为非负整数, a a a是正数, b b b和 c c c都是实数. 不过, 要是懂得多一点点, 就会在其中看到更多的可能, 包括但不限于多维和泛函, 因为我是真的不会了, 所以不在此赘述.
1.2 Maxwell-Blotzmann分布
然后是Maxwell(麦克斯韦)速率分布函数, 这个分布又称Maxwell-Boltzmann(玻尔兹曼)分布. 一言以蔽之, 它就是一个描述一定温度下微观粒子运动速度的概率分布函数. 它是个关于速率 v v v的概率密度函数(Probability Distribution Function), 也就是说, 这个函数 f ( v ) f(v) f(v)满足:
∫ − ∞ + ∞ f ( v ) d v = 1 \displaystyle\int_{-\infty}^{+\infty}f(v)\mathop{}\!\mathrm{d}v=1 ∫−∞+∞f(v)dv=1
而分布函数本体是长这个样子的:
f ( v ) = { 2 π ( m k B T ) 3 v 2 e − m v 2 2 k B T , v > 0 0 , v ≤ 0 \displaystyle f(v)=\begin{cases} \displaystyle\sqrt{\frac{2}{\pi}\left(\frac{m}{k_BT}\right)^3}v^2e^{-\frac{mv^2}{2k_BT}},\,&v>0\\ 0,\,&v\leq0\\\end{cases} f(v)=⎩⎪⎨⎪⎧π2(kBTm)3v2e−2kBTmv2,0,v>0v≤0
其中, m m m是每个分子的质量, T T T是绝对温度, v v v当然就是速率, 所以在 v < 0 v<0 v<0的时候概率密度都是 0 0 0, 而 k B k_B kB是Boltzmann常数, 或者, 就是 R N A \displaystyle\frac{R}{N_A} NAR, 分子上是我们熟知的理想气体常数, 分母上则是Avogadro(阿伏伽德罗)常数.
顺便一提, 在这个函数中, v = 0 v=0 v=0的情况被分在了下面, 就是直接是 0 0 0. 不过, 这完全不重要, 因为把 0 0 0代进上面的式子里面, 计算得到也是 0 0 0. 并且, 速率为 0 0 0的气体分子在非绝对零度的时候是不存在的.
如果我们需要计算平均速率的话, 我们就需要计算 E ( v ) E(v) E(v), 也就是 v v v的数学期望. 计算公式如下:
E ( v ) = ∫ − ∞ + ∞ f ( v ) v d v = ∫ 0 + ∞ 2 π ( m k B T ) 3 v 3 e − m v 2 2 k B T d v \begin{aligned}E(v)&=\int_{-\infty}^{+\infty}f(v)v\mathop{}\!\mathrm{d}v\\ &=\int_0^{+\infty}\sqrt{\frac{2}{\pi}\left(\frac{m}{k_BT}\right)^3}v^3e^{-\frac{mv^2}{2k_BT}}\mathop{}\!\mathrm{d}v\end{aligned} E(v)=∫−∞+∞f(v)vdv=∫0+∞π2(kBTm)3v3e−2kBTmv2dv
注意到, v 2 v^2 v2变成了 v 3 v^3 v3.
或者, 如果我们要计算方均根速率 v 2 ˉ \sqrt{\bar{v^2}} v2ˉ, 那么我们就需要先计算 E ( v 2 ) E(v^2) E(v2), 然后开根, 计算公式也是基本一致:
E ( v 2 ) = ∫ 0 + ∞ 2 π ( m k B T ) 3 v 4 e − m v 2 2 k B T d v \displaystyle E(v^2)=\int_0^{+\infty}\sqrt{\frac{2}{\pi}\left(\frac{m}{k_BT}\right)^3}v^4e^{-\frac{mv^2}{2k_BT}}\mathop{}\!\mathrm{d}v E(v2)=∫0+∞π2(kBTm)3v4e−2kBTmv2dv
可以看到, 这些广义积分都与Gauss积分有着很相似的形式, 其实也明示了只要我们知道Gauss积分怎么计算, 计算这些也就易如反掌.
2. 让我们开始吧
2.1 从最简单的Gauss积分开始
高楼平地起, 我们先从最最简单的形式, 计算 ∫ 0 + ∞ e − x 2 d x \displaystyle\int_{0}^{+\infty}e^{-x^2}\mathop{}\!\mathrm{d}x ∫0+∞e−x2dx开始. 注意到, 我们把下限换成了 0 0 0, 但是一点问题都没有, 因为Gauss函数显然是个偶函数, 要算全实数域上的积分只要乘以 2 2 2就行了, 并且实际上我们之后也主要是计算非负实数域上的积分, 这样反而更加便于之后的计算.
我们知道, 不是所有的函数都有初等原函数, 就比如我们的主角: e − x 2 e^{-x^2} e−x2. 但是, 我们也不是一定要有原函数才能计算积分值, 我们的主角又是个典型的例子. 不过, 为了算它, 我们会看到魔法一般的操作.
首先, 我们令这个积分的值为 I I I, 然后把这个积分平方, 变成:
I 2 = ∫ 0 + ∞ e − x 2 d x × ∫ 0 + ∞ e − x 2 d x \displaystyle I^2=\int_{0}^{+\infty}e^{-x^2}\mathop{}\!\mathrm{d}x\times\int_{0}^{+\infty}e^{-x^2}\mathop{}\!\mathrm{d}x I2=∫0+∞e−x2dx×∫0+∞e−x2dx
其次, 我们把后面那个积分中的 x x x全都换成 y y y, 这一步显然也没有问题.
⇒ I 2 = ∫ 0 + ∞ e − x 2 d x × ∫ 0 + ∞ e − y 2 d y \displaystyle\Rightarrow I^2=\int_{0}^{+\infty}e^{-x^2}\mathop{}\!\mathrm{d}x\times\int_{0}^{+\infty}e^{-y^2}\mathop{}\!\mathrm{d}y ⇒I2=∫0+∞e−x2dx×∫0+∞e−y2dy
然后, 根据Fubini-Tonelli(富比尼-托内利)定理, 我们可以把这个积分化为在 x O y xOy xOy平面上的对第一象限及其边界的重积分:
⇒ I 2 = ∫ 0 + ∞ ∫ 0 + ∞ e − ( x 2 + y 2 ) d x d y \displaystyle\Rightarrow I^2=\int_{0}^{+\infty}\int_{0}^{+\infty}e^{-\left(x^2+y^2\right)}\mathop{}\!\mathrm{d}x\mathop{}\!\mathrm{d}y ⇒I2=∫0+∞∫0+∞e−(x2+y2)dxdy
这里可能需要一点点的解释: 这个定理保证了上述两个积分的积可以转化为重积分, 但是这些细节在高等数学甚至是一些数学分析的课程中被隐藏了. 这个定理的描述和证明对本文没有太大意义, 并且可能会使得本文篇幅翻倍~~, 我会跟你说是因为我根本不会嘛~~, 所以就不继续解释了.
最后, 魔法开始了: 我们进行变量代换, 或者说坐标转换, 把平面直角坐标系化为极坐标系, 便有了下面的操作:
⇒ I 2 = ∫ 0 π 2 ∫ 0 + ∞ e − r 2 r d r d θ \Rightarrow I^2=\int_{0}^{\frac{\pi}{2}}\int_{0}^{+\infty}e^{-r^2}r\mathop{}\!\mathrm{d}r\mathop{}\!\mathrm{d}\theta ⇒I2=∫02π∫0+∞e−r2rdrdθ
因为做了变量代换, 我们在积分中乘了一个系数 r r r, 也正是这个 r r r, 使得这个广义积分突然变成了有原函数的积分.
可能需要再说明一下的是, 无穷积分只是个形式积分, 是对定积分取极限的结果, 所以直接认为两个积分域一样是有问题的. 但是, 我们可以通过夹逼保证两者是一样的. 简而言之, 一个半径为 r r r的 1 4 \displaystyle\frac{1}{4} 41圆可以被一个边长为 r r r的正方形所完全包围, 并且可以完全包围一个边长为 r 2 \displaystyle\frac{r}{\sqrt{2}} 2r的正方形.
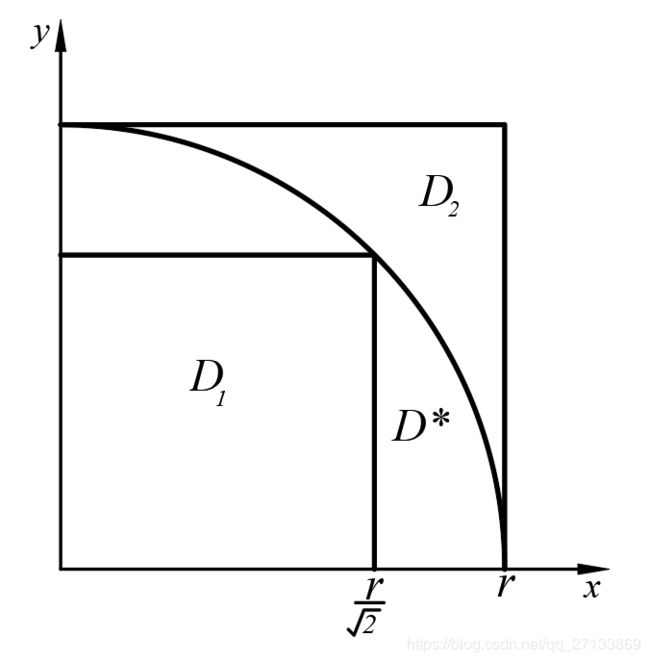
于是乎, 这个积分被秒了:
I 2 = 1 2 ∫ 0 π 2 d θ ∫ 0 + ∞ e − r 2 d r 2 = 1 2 × π 2 × 1 = π 4 , I = 1 2 π I^2=\frac{1}{2}\int_{0}^{\frac{\pi}{2}}\mathop{}\!\mathrm{d}\theta\int_{0}^{+\infty}e^{-r^2}\mathop{}\!\mathrm{d}r^2=\frac{1}{2}\times\frac{\pi}{2}\times1=\frac{\pi}{4},\,I=\frac{1}{2}\sqrt{\pi} I2=21∫02πdθ∫0+∞e−r2dr2=21×2π×1=4π,I=21π
顺便, 我们也有了:
∫ 0 + ∞ e − α x 2 d x = 1 2 π α \int_{0}^{+\infty}e^{-\alpha x^2}\mathop{}\!\mathrm{d}x=\frac{1}{2}\sqrt{\frac{\pi}{\alpha}} ∫0+∞e−αx2dx=21απ
这些操作看似都没什么, 但是合起来便是魔法, 所以也被作为经典的例子, 几乎每个多元微积分课上都会讲到. 这样, 是不是也对为什么标准正态分布的概率密度函数是 f ( x ) = 1 2 π e − x 2 2 \displaystyle f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} f(x)=2π1e−2x2感到恍然大雾悟了呢?
2.2 加大一点点力度——Gauss积分的广义形式
再回顾一下之前说的Gauss积分的广义形式:
∫ − ∞ + ∞ x n e − a x 2 + b x + c d x \displaystyle\int_{-\infty}^{+\infty}x^ne^{-ax^2+bx+c}\mathop{}\!\mathrm{d}x ∫−∞+∞xne−ax2+bx+cdx
它扩展的地方有二, 一个是加上了 x n x^n xn, 一个是 x 2 x^2 x2变成了普通的二次函数.
我们先来添个坑, 把只是把 x 2 x^2 x2换成普通的二次函数的情况来说说. 其实说起来也就一句话:
∫ − ∞ + ∞ e − a x 2 + b x + c d x = ∫ − ∞ + ∞ e − a ( x − b 2 a ) 2 + c + b 2 4 a d ( x − b 2 a ) = π a e b 2 4 a + c \displaystyle\int_{-\infty}^{+\infty}e^{-ax^2+bx+c}\mathop{}\!\mathrm{d}x=\int_{-\infty}^{+\infty}e^{-a(x-\frac{b}{2a})^2+c+\frac{b^2}{4a}}\mathop{}\!\mathrm{d}(x-\frac{b}{2a})=\sqrt{\frac{\pi}{a}}e^{\frac{b^2}{4a}+c} ∫−∞+∞e−ax2+bx+cdx=∫−∞+∞e−a(x−2ab)2+c+4ab2d(x−2ab)=aπe4ab2+c
啥? 你问如果积分域是非负实数的时候? 我不会, 对不起打扰告辞了.
接着, 我们向 ∫ 0 + ∞ x n e − α x 2 d x \displaystyle\int_{0}^{+\infty}x^ne^{-\alpha x^2}\mathop{}\!\mathrm{d}x ∫0+∞xne−αx2dx进发. 事先说一下, 我们只考虑 n n n是非负整数的时候. 要不是我菜, 我会不讲么.
当 n = 0 n=0 n=0的时候, 那就直接抄个上面的结果. 要是 n = 1 n=1 n=1的话, 就可以直接凑一手微分然后得到结果:
∫ 0 + ∞ x e − α x 2 d x = 1 2 ∫ 0 + ∞ e − α x 2 d ( x 2 ) = 1 2 α \int_{0}^{+\infty}xe^{-\alpha x^2}\mathop{}\!\mathrm{d}x=\frac{1}{2}\int_{0}^{+\infty}e^{-\alpha x^2}\mathop{}\!\mathrm{d}\left(x^2\right)=\frac{1}{2\alpha} ∫0+∞xe−αx2dx=21∫0+∞e−αx2d(x2)=2α1
要是 n ≥ 2 n\geq2 n≥2, 并且 n n n是个奇数的话, 假设 n = 2 m + 1 n=2m+1 n=2m+1, 就可以变量代换: t = x 2 t=x^2 t=x2, 然后分部积分:
∫ 0 + ∞ x n e − α x 2 d x = 1 2 ∫ 0 + ∞ x 2 m e − α x 2 d ( x 2 ) = 1 2 ∫ 0 + ∞ t m e − α t d t = − 1 2 α t m e − α t ∣ 0 + ∞ + m 2 α ∫ 0 + ∞ t m − 1 e − α t d t = 0 − 0 + m 2 α ∫ 0 + ∞ t m − 1 e − α t d t = ⋯ = m ! 2 α m + 1 \begin{aligned}\int_{0}^{+\infty}x^ne^{-\alpha x^2}\mathop{}\!\mathrm{d}x=&\frac{1}{2}\int_{0}^{+\infty}x^{2m}e^{-\alpha x^2}\mathop{}\!\mathrm{d}\left(x^2\right)=\frac{1}{2}\int_{0}^{+\infty}t^me^{-\alpha t}\mathop{}\!\mathrm{d}t\\ =&-\left.\frac{1}{2\alpha}t^me^{-\alpha t}\right|_0^{+\infty}+\frac{m}{2\alpha}\int_0^{+\infty}t^{m-1}e^{-\alpha t}\mathop{}\!\mathrm{d}t\\ =&0-0+\frac{m}{2\alpha}\int_0^{+\infty}t^{m-1}e^{-\alpha t}\mathop{}\!\mathrm{d}t=\cdots\\ =&\frac{m!}{2\alpha^{m+1}} \end{aligned} ∫0+∞xne−αx2dx====21∫0+∞x2me−αx2d(x2)=21∫0+∞tme−αtdt−2α1tme−αt∣∣∣∣0+∞+2αm∫0+∞tm−1e−αtdt0−0+2αm∫0+∞tm−1e−αtdt=⋯2αm+1m!
最麻烦的是当 n n n是正偶数的时候, 虽然我们已经把最复杂的部分做完了, 剩下的基本上就是朝死里分部积分. 首先, 我们令 I ( n ) = I ( 2 m ) = ∫ 0 + ∞ x 2 m e − α x 2 d x \displaystyle I(n)=I(2m)=\int_{0}^{+\infty}x^{2m}e^{-\alpha x^2}\mathop{}\!\mathrm{d}x I(n)=I(2m)=∫0+∞x2me−αx2dx, 然后还是老样子:
I ( n ) = I ( 2 m ) = ∫ 0 + ∞ x 2 m e − α x 2 d x = 1 2 ∫ 0 + ∞ x 2 m − 1 e − α x 2 d ( x 2 ) = − 1 2 α x 2 m − 1 e − α x 2 ∣ 0 + ∞ + 2 m − 1 2 α ∫ 0 + ∞ x 2 m − 2 e − α x 2 d x = 0 − 0 + 2 m − 1 2 α ∫ 0 + ∞ x 2 m − 2 e − α x 2 d x = 2 m − 1 2 α I ( 2 ( m − 1 ) ) = ⋯ = ( 2 m − 1 ) ! ! ( 2 α ) m ∫ 0 + ∞ e − x 2 d x = ( 2 m − 1 ) ! ! 2 m + 1 α m π α \begin{aligned}I(n)=I(2m)=&\int_{0}^{+\infty}x^{2m}e^{-\alpha x^2}\mathop{}\!\mathrm{d}x=\frac{1}{2}\int_{0}^{+\infty}x^{2m-1}e^{-\alpha x^2}\mathop{}\!\mathrm{d}\left(x^2\right)\\ =&\left.-\frac{1}{2\alpha}x^{2m-1}e^{-\alpha x^2}\right|_0^{+\infty}+\frac{2m-1}{2\alpha}\int_{0}^{+\infty}x^{2m-2}e^{-\alpha x^2}\mathop{}\!\mathrm{d}x\\ =&0-0+\frac{2m-1}{2\alpha}\int_{0}^{+\infty}x^{2m-2}e^{-\alpha x^2}\mathop{}\!\mathrm{d}x=\frac{2m-1}{2\alpha}I(2(m-1))=\cdots\\ =&\frac{(2m-1)!!}{(2\alpha)^m}\int_{0}^{+\infty}e^{-x^2}\mathop{}\!\mathrm{d}x=\frac{(2m-1)!!}{2^{m+1}\alpha^m}\sqrt{\frac{\pi}{\alpha}} \end{aligned} I(n)=I(2m)====∫0+∞x2me−αx2dx=21∫0+∞x2m−1e−αx2d(x2)−2α1x2m−1e−αx2∣∣∣∣0+∞+2α2m−1∫0+∞x2m−2e−αx2dx0−0+2α2m−1∫0+∞x2m−2e−αx2dx=2α2m−1I(2(m−1))=⋯(2α)m(2m−1)!!∫0+∞e−x2dx=2m+1αm(2m−1)!!απ
其中, ! ! !! !!表示双阶乘, 在正整数域上定义为:
n ! ! = { n × ( n − 2 ) × ⋯ × 2 , n ≡ 0 m o d 2 n × ( n − 2 ) × ⋯ × 1 , n ≡ 1 m o d 2 n!!=\begin{cases} n\times(n-2)\times\cdots\times2,\,&n\equiv0\mod2\\ n\times(n-2)\times\cdots\times1,\,&n\equiv1\mod2\\ \end{cases} n!!={n×(n−2)×⋯×2,n×(n−2)×⋯×1,n≡0mod2n≡1mod2
比如说 4 ! ! = 4 × 2 = 8 4!!=4\times2=8 4!!=4×2=8, 或者 5 ! ! = 5 × 3 × 1 = 15 5!!=5\times3\times1=15 5!!=5×3×1=15.
至此, 我们就把这些情况基本全部讨论了一遍, 至于最复杂的那种情况, 我好像真的不会, 就饶了我吧. 反正现在这些东西已经够我们算我们想要算的东西了对吧.
2.3 来做亿点习题吧——Maxwell-Boltzmann分布的平均速度
首先, 我们回到初心, 来康康Maxwell-Boltzmann分布的平均速度怎么算吧. 套, 都可以套(指公式)
v ˉ = E ( v ) = ∫ − ∞ + ∞ f ( v ) v d v = ∫ 0 + ∞ 2 π ( m k B T ) 3 v 3 e − m v 2 2 k B T d v = 2 π ( m k B T ) 3 × 1 2 ( 2 k B T m ) 2 = 2 2 k B T π m \begin{aligned}\bar{v}=E(v)=&\int_{-\infty}^{+\infty}f(v)v\mathop{}\!\mathrm{d}v=\int_0^{+\infty}\sqrt{\frac{2}{\pi}\left(\frac{m}{k_BT}\right)^3}v^3e^{-\frac{mv^2}{2k_BT}}\mathop{}\!\mathrm{d}v\\ =&\sqrt{\frac{2}{\pi}\left(\frac{m}{k_BT}\right)^3}\times\frac{1}{2}\left(\frac{2k_BT}{m}\right)^2=2\sqrt{\frac{2k_BT}{\pi m}} \end{aligned} vˉ=E(v)==∫−∞+∞f(v)vdv=∫0+∞π2(kBTm)3v3e−2kBTmv2dvπ2(kBTm)3×21(m2kBT)2=2πm2kBT
虽然自己推一遍公式很爽, 但是套自己推的公式还是更爽啊, 让我们再套一次: 这回算一手方均根速率 v 2 ˉ \displaystyle\sqrt{\bar{v^2}} v2ˉ:
v 2 ˉ = E ( v 2 ) = ∫ − ∞ + ∞ f ( v ) v 2 d v = ∫ 0 + ∞ 2 π ( m k B T ) 3 v 4 e − m v 2 2 k B T d v = 2 π ( m k B T ) 3 × ( 4 − 1 ) ) ! ! 2 2 + 1 ( 2 k B T m ) 2 π 2 k B T m = 3 k B T m \begin{aligned}\bar{v^2}=E\left(v^2\right)=&\int_{-\infty}^{+\infty}f(v)v^2\mathop{}\!\mathrm{d}v=\int_0^{+\infty}\sqrt{\frac{2}{\pi}\left(\frac{m}{k_BT}\right)^3}v^4e^{-\frac{mv^2}{2k_BT}}\mathop{}\!\mathrm{d}v\\ =&\sqrt{\frac{2}{\pi}\left(\frac{m}{k_BT}\right)^3}\times\frac{(4-1))!!}{2^{2+1}}\left(\frac{2k_BT}{m}\right)^2\sqrt{\frac{\pi2k_BT}{m}}=3\frac{k_BT}{m} \end{aligned} v2ˉ=E(v2)==∫−∞+∞f(v)v2dv=∫0+∞π2(kBTm)3v4e−2kBTmv2dvπ2(kBTm)3×22+1(4−1))!!(m2kBT)2mπ2kBT=3mkBT
于是方均根速率就是: v 2 ˉ = 3 k B T m \displaystyle\sqrt{\bar{v^2}}=\sqrt{\frac{3k_BT}{m}} v2ˉ=m3kBT.
然后我们梅开三度, 不如验证一下这个速率分布函数满足规范性?
∫ − ∞ + ∞ f ( v ) d v = ∫ 0 + ∞ 2 π ( m k B T ) 3 v 2 e − m v 2 2 k B T d v = 2 π ( m k B T ) 3 × ( 2 − 1 ) ) ! ! 2 1 + 1 2 k B T m π 2 k B T m = 1 \begin{aligned}\int_{-\infty}^{+\infty}f(v)\mathop{}\!\mathrm{d}v=&\int_0^{+\infty}\sqrt{\frac{2}{\pi}\left(\frac{m}{k_BT}\right)^3}v^2e^{-\frac{mv^2}{2k_BT}}\mathop{}\!\mathrm{d}v\\ =&\sqrt{\frac{2}{\pi}\left(\frac{m}{k_BT}\right)^3}\times\frac{(2-1))!!}{2^{1+1}}\frac{2k_BT}{m}\sqrt{\frac{\pi2k_BT}{m}}=1 \end{aligned} ∫−∞+∞f(v)dv==∫0+∞π2(kBTm)3v2e−2kBTmv2dvπ2(kBTm)3×21+1(2−1))!!m2kBTmπ2kBT=1
3. 亿点点拓展: Γ \Gamma Γ函数
其实, 对于积分 ∫ 0 + ∞ x n e − α x 2 d x \displaystyle\int_{0}^{+\infty}x^ne^{-\alpha x^2}\mathop{}\!\mathrm{d}x ∫0+∞xne−αx2dx, 上面写的那几种对不同的 n n n所得到的不同形式的结果, 是可以化成统一的形式的.
我们略去构造性证明是因为我不会, 直接给出结果, 然后再进行验证:
∫ 0 + ∞ x n e − α x 2 d x = Γ ( n + 1 2 ) 2 a n + 1 2 \int_{0}^{+\infty}x^ne^{-\alpha x^2}\mathop{}\!\mathrm{d}x=\frac{\Gamma(\frac{n+1}{2})}{2a^{\frac{n+1}{2}}} ∫0+∞xne−αx2dx=2a2n+1Γ(2n+1)
其中, Γ ( z ) = ∫ 0 + ∞ t z − 1 e − t d t , z ∈ C , ℜ ( z ) > 0 \displaystyle\Gamma(z)=\int_0^{+\infty}t^{z-1}e^{-t}\mathop{}\!\mathrm{d}t,\,z\in\mathbb{C},\,\Re(z)>0 Γ(z)=∫0+∞tz−1e−tdt,z∈C,ℜ(z)>0, 名为 Γ \Gamma Γ(Gamma)函数, 定义在除去零和负实数的复数域上.
我们通过反推, 可以发现对于任意正整数 n n n, 有 Γ ( n ) = ( n − 1 ) ! \Gamma(n)=(n-1)! Γ(n)=(n−1)!, 而对于任意 1 2 \displaystyle\frac{1}{2} 21的正奇数倍 m m m, Γ ( m ) = ( m − 1 ) × ( m − 2 ) × ⋯ × 1 2 × π \displaystyle\Gamma(m)=(m-1)\times(m-2)\times\cdots\times\frac{1}{2}\times\sqrt{\pi} Γ(m)=(m−1)×(m−2)×⋯×21×π. 那这两个还能接着统一嘛? 当然是可以的. 通过观察发现, 对于任意 1 2 \displaystyle\frac{1}{2} 21的正整数倍 n n n, 有 Γ ( n + 1 ) = n Γ ( n ) \Gamma(n+1)=n\Gamma(n) Γ(n+1)=nΓ(n).
所以, 我们来快速地证明一下这些东西:
Γ ( z + 1 ) = ∫ 0 + ∞ t z e − t d t = − t z e − t ∣ 0 + ∞ + z ∫ 0 + ∞ t z − 1 e − t d t = 0 − 0 + z ∫ 0 + ∞ t z − 1 e − t d t = z Γ ( z ) \begin{aligned}\Gamma(z+1)=&\int_0^{+\infty}t^ze^{-t}\mathop{}\!\mathrm{d}t=\left.-t^ze^{-t}\right|_{0}^{+\infty}+z\int_{0}^{+\infty}t^{z-1}e^{-t}\mathop{}\!\mathrm{d}t\\ =&0-0+z\int_{0}^{+\infty}t^{z-1}e^{-t}\mathop{}\!\mathrm{d}t=z\Gamma(z)\\ \end{aligned} Γ(z+1)==∫0+∞tze−tdt=−tze−t∣∣0+∞+z∫0+∞tz−1e−tdt0−0+z∫0+∞tz−1e−tdt=zΓ(z)
然后, 我们只要算一下 Γ ( 1 ) \Gamma(1) Γ(1)和 Γ ( 1 2 ) \displaystyle\Gamma(\frac{1}{2}) Γ(21)就可以了:
Γ ( 1 ) = ∫ 0 + ∞ t 0 e − t d t = − e t ∣ 0 ∞ = 1 Γ ( 1 2 ) = ∫ 0 + ∞ t − 0.5 e − t d t = 2 ∫ 0 + ∞ e − t 2 1 2 t d t = 2 ∫ 0 + ∞ e − t 2 d t = π \begin{aligned} \Gamma(1)=&\int_0^{+\infty}t^0e^{-t}\mathop{}\!\mathrm{d}t=\left.-e^t\right|_0^{\infty}=1\\ \Gamma(\frac{1}{2})=&\int_0^{+\infty}t^{-0.5}e^{-t}\mathop{}\!\mathrm{d}t=2\int_0^{+\infty}e^{-\sqrt{t}^2}\frac{1}{2\sqrt{t}}\mathop{}\!\mathrm{d}t=2\int_0^{+\infty}e^{-\sqrt{t}^2}\mathop{}\!\mathrm{d}\sqrt{t}=\sqrt{\pi} \end{aligned} Γ(1)=Γ(21)=∫0+∞t0e−tdt=−et∣∣0∞=1∫0+∞t−0.5e−tdt=2∫0+∞e−t22t1dt=2∫0+∞e−t2dt=π
其中在算 Γ ( 1 2 ) \displaystyle\Gamma(\frac{1}{2}) Γ(21)的时候, 我们又用了一次最开始算过的Gauss积分.
至此, 证明完毕.
4. 结语
本文以大学物理中会遇到的Maxwell速率分布函数为切入点, 求它的方均根速率其实就是涉及到了概率统计中的数学期望, 而算这个数学期望就要用到高等数学中的Gauss积分.
所以本文先介绍了Gauss积分的狭义形式和广义形式的概念及其计算, 然后我们用Gauss积分来计算方均根速率, 最后我们又拓展介绍了一下 Γ \Gamma Γ函数.
虽然全文的内容对高数和大物, 当然还有概统, 都没有什么实质性的帮助, 但是在文章的最开始也说了: 这仅仅是想知其所以然罢了. 知道其中的所以然, 从非功利的角度来说, 希望这篇博客能对大家有一定的启发.