opencv 分水岭算法

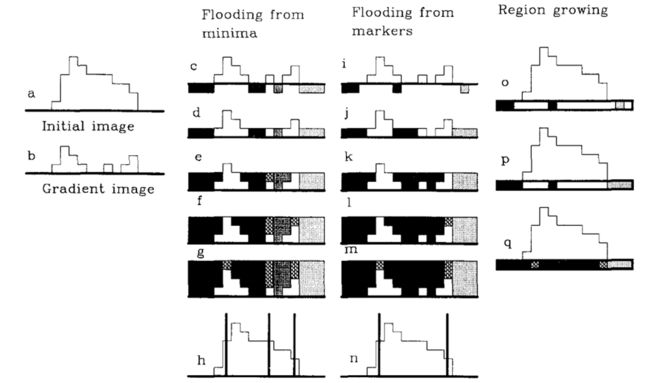
分水岭在地理学上就是指一个山脊，水通常会沿着山脊的两边流向不同的“汇水盆”。分水岭算法是一种用于图像分割的经典算法，是基于拓扑理论的数学形态学的分割方法。如果图像中的目标物体是连在一起的，则分割起来会更困难，分水岭算法经常用于处理这类问题，通常会取得比较好的效果。
那我们先来看一下opencv当中，分水岭算法watershed的实现。
opencv的watershed是在Meyer, F.Color Image Segmentation, ICIP92,1992的基础上实现的。

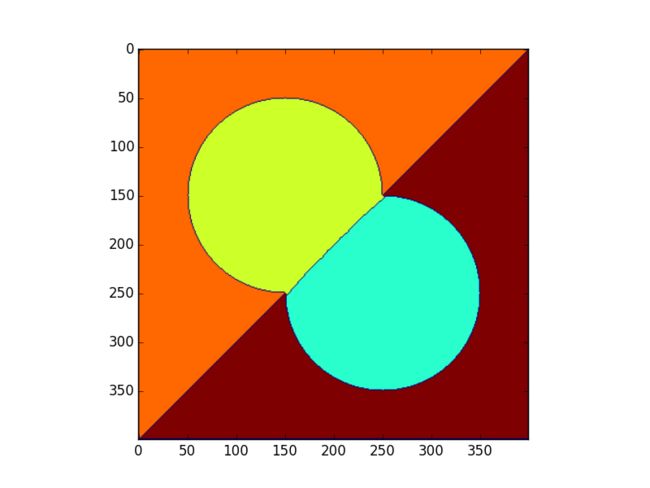
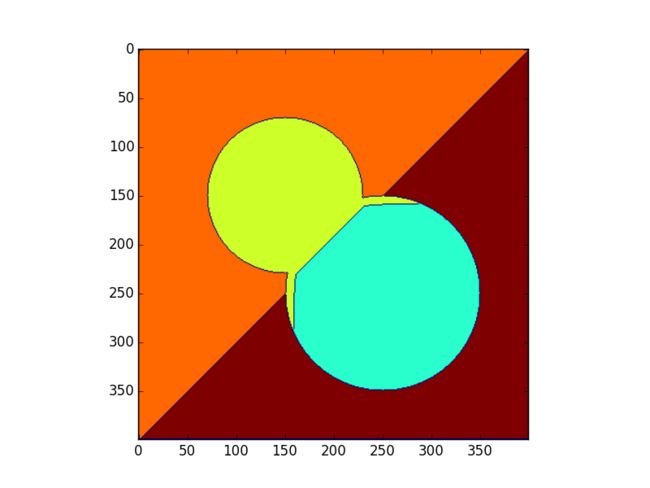
注意，我们这里传入了两个参数，一个是原始图片(a)，一个是种子点的坐标。
原始图片的梯度图(b)实际上是在这个函数内部生成的，上图中给出了信息：当我们选取n个种子点，整个图像会被分割成n + 1块。

算法流程：

1. 首先得到mark标记图，全部标记为0，然后依次将种子点的值标记到mark图上分别为1，2…L，再标记分水岭区域为-1（图像边界预先标记为分水岭，一些我们不希望做出分割的部位）

这里的图像边界请格外注意：我们会把图像第一行和最后一行置为分水岭(shed = -1)，我们还会把图像最后一列和第一咧置为分水岭(shed = -1)，这意味着如果我们在这些边界点的marker上写上我们的分分类标签，这跟没写一样，因为函数内部还是会覆盖这些标签数据

1. 将种子点的四邻域加入到优先级队列（小根堆），取决于当前种子点与四邻域之间的灰度值的差的绝对值，（如果这是一张彩色图像，我们就把三个通道分别的差的绝对值的最大值作为判断标准）

while(!queue.empty())
   cur = queue.front();
   if(4邻域某个域等于０)
   ｛
       以cur的种子值标记4邻域某个域
       queue.push(当前域)
　　｝
   else if(4邻域某个域不等于０　且　不等于cur的种子值)
       那么画地为界，该像素充当分水岭，标记为-1

算法应用：

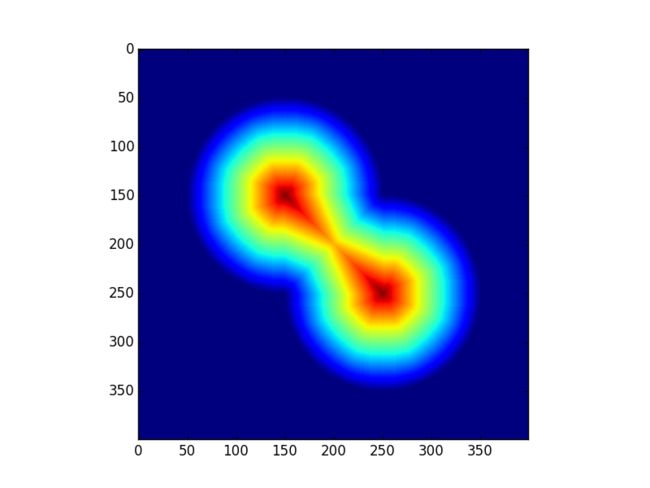
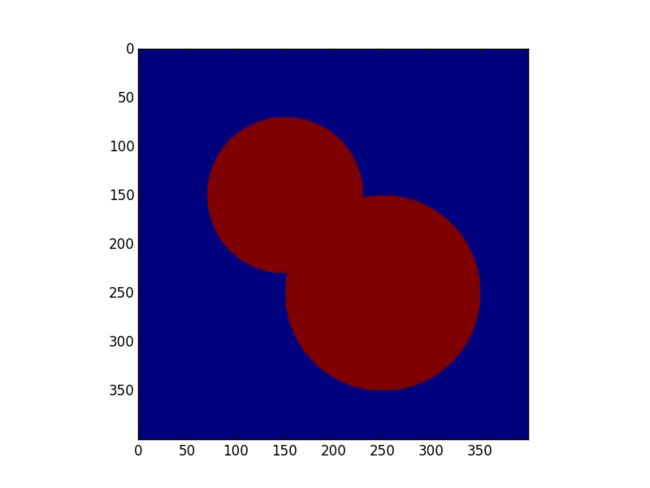
分水岭算法可以和距离变换结合，寻找“汇水盆地”和“分水岭界限”，从而对图像进行分割。二值图像的距离变换就是每一个像素点到最近非零值像素点的距离。

在下面的例子中，需要将两个重叠的圆分开。

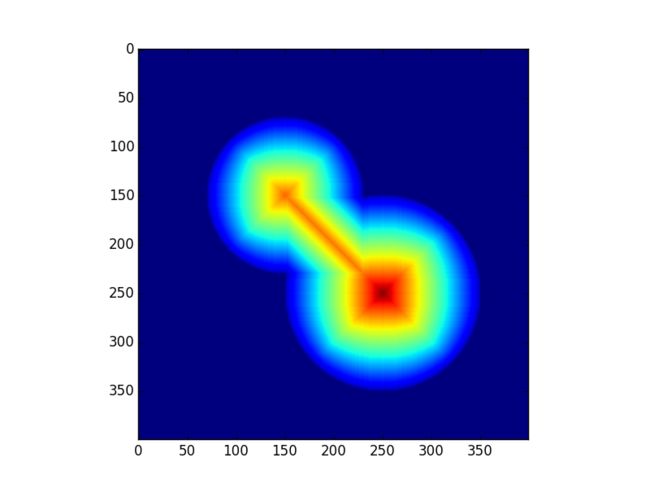
我们先计算圆上的这些白色像素点到黑色背景像素点的距离变换。

mask_size:CV_DIST_MASK_PRECISE

mask_size:CV_DIST_MASK_3

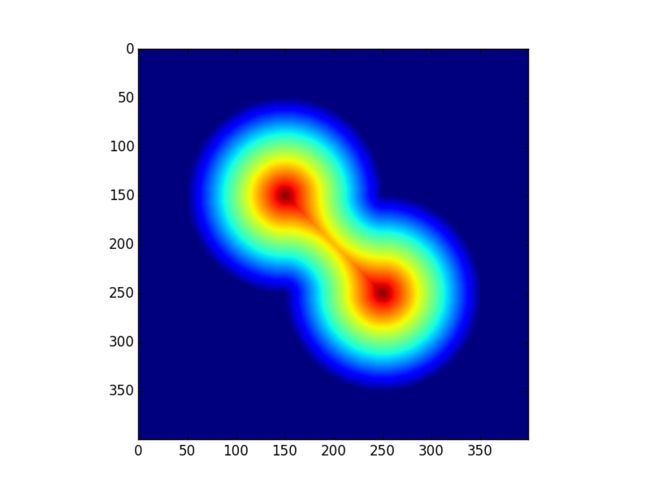
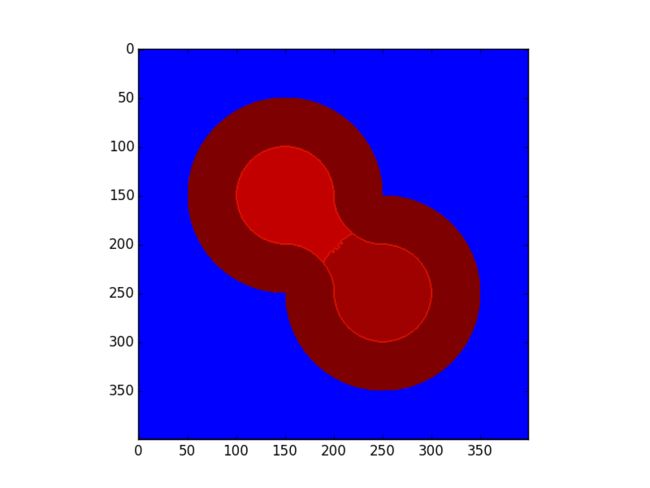
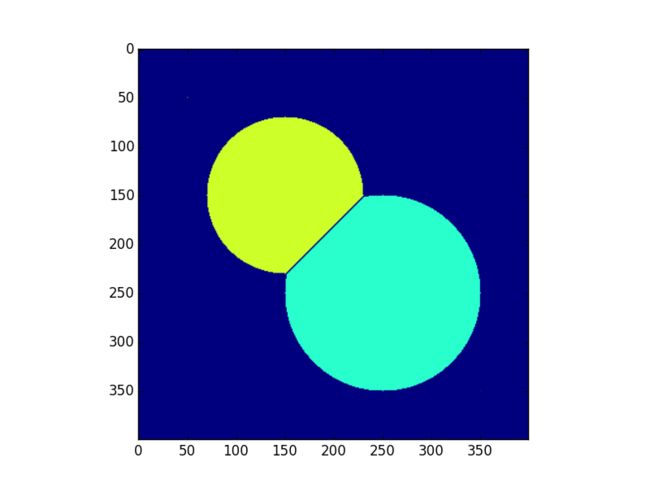
选出距离变换中的最大值作为初始标记点，从这些标记点开始的两个汇水盆越集越大，最后相交于分山岭。从分山岭处断开，我们就得到了两个分离的圆。

mask_size:CV_DIST_MASK_PRECISE

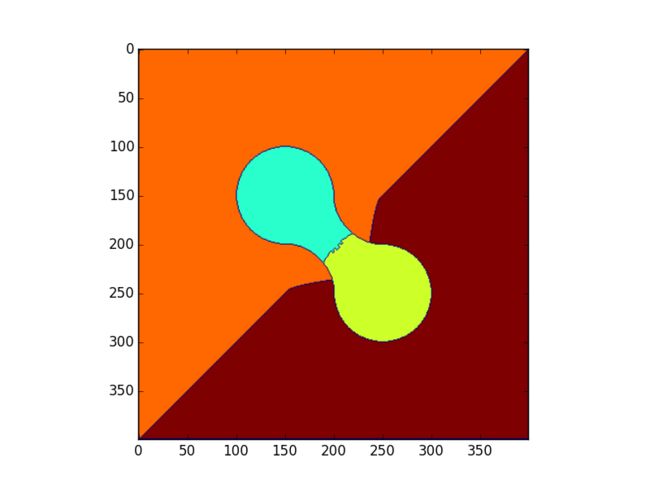
mask_size:CV_DIST_MASK_3

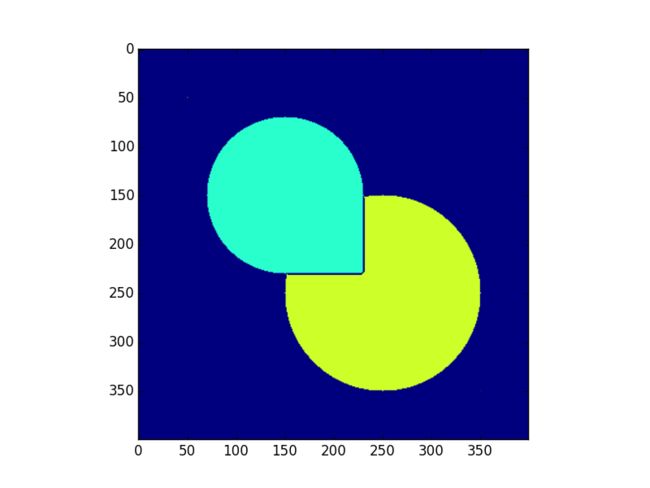
诶，非常奇怪，怎嘛会这样？
让我们先来看一下代码：

这里先插入一下opencv的distance type：
CV_DIST_USER =-1, /* User defined distance */
CV_DIST_L1 =1, /* distance = |x1-x2| + |y1-y2| */
CV_DIST_L2 =2, /* the simple euclidean distance */
CV_DIST_C =3, /* distance = max(|x1-x2|,|y1-y2|) */
CV_DIST_L12 =4, /* L1-L2 metric: distance = 2(sqrt(1+x*x/2) - 1)) */
CV_DIST_FAIR =5, /* distance = c^2(|x|/c-log(1+|x|/c)), c = 1.3998 */
CV_DIST_WELSCH =6, /* distance = c^2/2(1-exp(-(x/c)^2)), c = 2.9846 */
CV_DIST_HUBER =7 /* distance = |x|

import cv2
import matplotlib.pyplot as plt
import numpy as np
from Queue import PriorityQueue

#我们在下面自行创建了原始图片
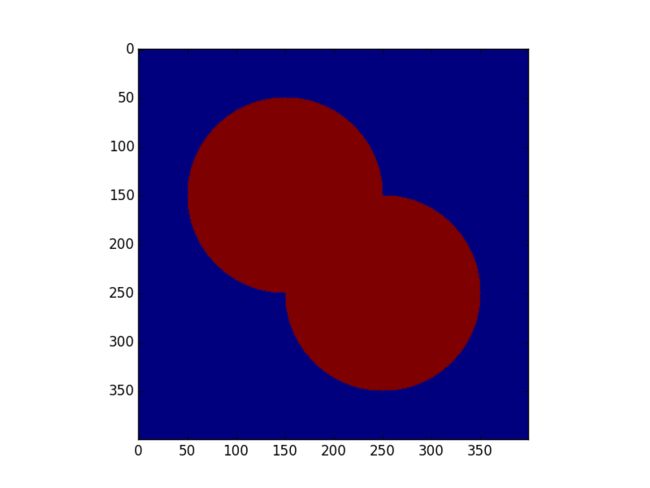
img = np.zeros((400, 400), np.uint8)
cv2.circle(img, (150, 150), 100, 255, -1)
cv2.circle(img, (250, 250), 100, 255, -1)

#进行了距离变换
dist = cv2.distanceTransform(img, cv2.cv.CV_DIST_L2, cv2.cv.CV_DIST_MASK_3)#euclidean distance

#单通道向三通道转换，watershed只接受三通道的图像
dist3 = np.zeros((dist.shape[0], dist.shape[1], 3), dtype = np.uint8)
dist3[:, :, 0] = dist
dist3[:, :, 1] = dist
dist3[:, :, 2] = dist

#创建分类的图层，包含种子点
markers = np.zeros(img.shape, np.int32)
cv2.circle(markers, (150, 150), 100, 0, -1)
cv2.circle(markers, (250, 250), 100, 0, -1)
markers[150,150] = 1 # seed for circle one
markers[250, 250] = 2 # seed for circle two
markers[50, 50] = 3 # seed for background
markers[350, 350] = 4 # seed for background

#执行分水岭算法
cv2.watershed(dist3, markers)
plt.imshow(markers)
plt.show()

但如果我们仔细看过上面的原理分析，就会发现分水岭内部是通过判断梯度来决定下一个种子点的选择的。
在那张距离变换的图上，背景部分的梯度永远都是0，所以背景部分会优先与山峰部分被标记，知道背景部分遇到了山峰的边缘部分，这个时候的梯度跟山顶部分的梯度相当，这时，山顶的种子才有可能后的向四临域泛洪的机会，所以两个种子的标签类最终会在山腰部分相遇，形成分水岭，这个山腰大概是１／２圆半径的位置。

解释到了这里，相信大家都知道发生了说明情况，分水岭是借助于原始图像的梯度来驱动的，这对自然生成的图片而言，能较有效的分割前景和背景，但对于这种靠距离变换生成的图形，其实有很大的问题。

那么我们要怎嘛解决呢？
其实解决方案可以很简单，遇到山脚的时候，山顶的才有机会执行，如果我们让山脚跟背景的高度差比较大，那么山脚下的种子点再之后将不会再获得执行的机会。

dist[dist > 0.0] += 5.0

分割的有点奇怪，这里的原因是因为实际上的关于欧几里得距离变换的计算是一种近似的计算，得到的并不是精确解，所以分割会出现毛刺的问题。

当然，如果我们采用能得到精确解的距离变换时，比如说cityBlock时

我们能够得到非常漂亮的分割，这也从侧面证明了之前的分割的毛刺问题是由于近似解引起的。

但更一般的图片会出现如下的情况：

这时候我们再应用上面的算法时，得到的精确的距离变换：

dist = cv2.distanceTransform(img, cv2.cv.CV_DIST_L1, cv2.cv.CV_DIST_MASK_3)

结果得到了这样的分割结果：

这样的结果肯定不是我们想要的，但结果从侧面告诉我们opencv的watershed采用的是基于梯度的应用。

所以对于这类图片的分割，我们需要利用基于深度的watershed

def watershed(dist, markers, markersList):#in order to change the way to choose gradient
    directR = [0, 1, 0, -1]
    directC = [-1, 0, 1, 0]
    pq = PriorityQueue()
    shed = -1
    height, width = dist.shape
    index = 0
    for seed in markersList:
        row = seed[0]
        col = seed[1]
        pq.put((dist[row][col], index, markers[row][col], row, col)) 
        print 'seed: ', dist[row][col]
    '''
    for row in xrange(height):
        for col in xrange(width):
            if markers[row][col] > 0:
                pq.put((dist[row][col], markers[row][col], row, col))#value, class, row, col
    '''
    mid = 0
    while not pq.empty():
        seed = pq.get()
        row = seed[3]
        col = seed[4]
        classType = seed[2]
        for curD in range(4):
            rowC = row + directR[curD]
            colC = col + directC[curD]
            if rowC < height and rowC >= 0 and colC < width and colC >= 0:#inreach
                if markers[rowC][colC] == 0:#unlabeled
                    markers[rowC][colC] = classType
                    index += 1
                    pq.put((dist[rowC][colC], index, markers[rowC][colC], rowC, colC))
                elif markers[rowC][colC] != shed and markers[rowC][colC] != classType:
                    markers[rowC][colC] = shed#boundery

这里需要特别注意的是：python的元组之间的比较规则，比较在第一个能够比较的元素开始

a = (1, [1, 2])
b = (1, [2, 2])
c = (2, [1, 2])
d = (1, [1, 1])

In [5]: a < b
Out[5]: True

In [6]: a > d
Out[6]: True

In [7]: c > a
Out[7]: True

之前我们放进优先队列的是深度，类别编号，行号，列号

pq.put((dist[row][col], markers[row][col], row, col)) 

所以当出现深度相同时，类别编号比较小的会优先出堆，这就造成了这样的一个情况：

markers[150,150] = 2 # seed for circle one
markers[250, 250] = 1 # seed for circle two

markers[150,150] = １ # seed for circle one
markers[250, 250] = ２ # seed for circle two

所以为了能够让相同深度的种子能够按照进入优先队列的顺序（两个山峰相同深度的种子交替出队），我们为放入优先队列的结节添加了进入队列的顺序编号。

pq.put((dist[row][col], index, markers[row][col], row, col))