Codeforces Round #410 (Div. 2)
https://codeforces.com/contest/798
https://codeforces.com/contest/798/problem/E
题意：
排列p，编码了一个序列a。对于每个i，找到第一个pj>pi并且未被标记的j，标记这个j并a[i]=j。给出a求一个可行的p，保证有解。n≤500000
思路:
仔细想了一个多小时，
思路是这样的，在原图中有两种关系。
第一种: 就是非常直接的
比如：
2 4 5 -1 -1
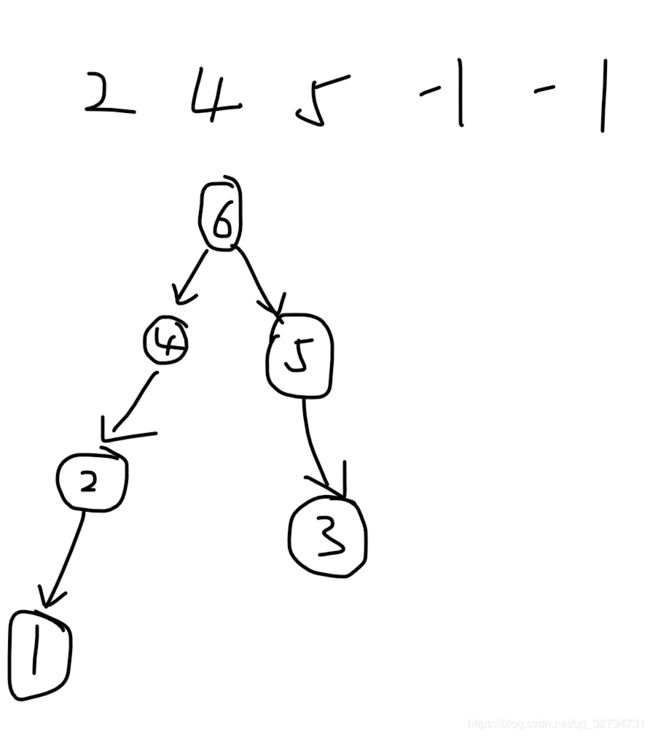首先画一个这种狗样子的图。这是他们的直接关系。
然后其实 -1没什么，-1只是说明 前面的n个位置，没有找到未被标记且比它大的数字了。所以比它大的数字肯定是n+1了。
然后在这个数组里面去寻找第二层关系。放到图里面
（2 ，4， 5， -1 ，-1 ）；
我们看 第一个位置 ，这个位置并看不出什么，所以 我们看第二个位置。
第二个位置是4 ，所以代表的事情是 ，前面三个数里面。第二个位置是最大的。(其余数未被标记时)
第三个数字，就是 前面四个数字里面。除了位置3本身，其余未被标记的，第三个数字最大。
这是个隐性关系。然后这个题就突然变水了。
为了清晰 ，把整个图补充完整。
第三个位置大于第一个位置
第二个位置大于第三个位置
第四个位置大于第五个位置
然后这个题目的答案就非常清晰了。
中间红线部分的关系怎么寻找是本题最需要的算法。
如果遍历寻找的话，直接就是n^2 ,虽然遍历图的复杂度是o(n)的。
所以今天又重新学了一遍拓扑排序
第二种关系。隐形关系的寻找。
可以直接这么概括。
如果a[x]==y 那么在y-1的位置中，未被标记的点种，x是最大的。
所以我们在寻找边的时候，直接寻找 y-1位置里面，未被标记的位置。
这点可以使用线段树去维护 ；
所以 这个题的题解是这个样子的。
快速寻找拓扑图的时候，是要去找，此前未被标记的点。 因为此前未被标记的点一定比这个点小。
然后 此前未被标记的点，一定会被当前点后面的标记的时候，这个点才确定不会在当前点之前标记。
8
2 -1 4 -1 6 -1 8 -1
1 8 2 7 3 6 4 5
比如样例，
其中 2 4 6 8 已经被标记
1 3 5 7 未被标记。
但是1 3 5 7 并没有被其余的任何点标记，
这时候，我们默认这几个点是被大于任何点的点标记的。
以此来维护
当 jp[j] &&k>i &&p[j]>p[i] 这种去寻找i之前未标记的点的状态。
#include
using namespace std;
const int maxn=5e5+5;
int a[maxn],b[maxn]; //使用b数组，去代表b[x] 被哪个数标记了。
int n;
pair tree[maxn*4];
#define mp make_pair
void update(int l,int r,int t,int v,int s)
{
if(l==r)
{
tree[t]=make_pair(s,l);
return ;
}
int mid=(l+r)/2;
if(v<=mid) update(l,mid,t*2 ,v,s );
else update(mid+1,r , t*2+1 ,v,s);
tree[t]=max(tree[t*2] , tree[ t*2+1 ] ) ;
}
pair query(int l,int r,int left,int right,int t)
{
if(left>right) return mp(0,0);
if( left<=l&&r<=right )
return tree[t];
int mid=(l+r)/2;
pair ae = query(l,mid, max(left,l) ,min(right,mid),t*2);
pair be = query( mid+1,r,max(mid+1,left),min(r, right) , t*2+1);
return max(ae,be);
}
int tag[maxn] ;
vector arr;
void dfs(int node)
{
if(tag[node]) return ;
update(1,n,1,node,0);
tag[node]=1;
if(b[node]!=n+1 )
dfs(b[node]);
while(1)
{
pair mx= query(1,n,1,a[node]-1,1 ); //去寻找a[node] 此前 未被标记过的点，也就是绝对小于a[node] 的点。
if(mx.first>node)
{
// cout<>n)
{
memset(b,0,sizeof(b));
for(int i=1;i<=n;i++)
{
cin>>a[i];
if(a[i]!=-1 ) b[a[i] ] =i; //b数组被哪个数字标记
else a[i]= n+1 ;//如果不标记任何数，则代表标记n+1
// cout<