哈夫曼树以及文件压缩的实现
一、HuffmanTree
哈夫曼树也称为最优二叉树,是加权路径长度最短的二叉树。在讲述哈夫曼树之前先给出几个概念:
路径:从一个结点到一个结点之间的分支构成这两个结点之间的路径
路径长度:路径上分支的数目称为路径长度
树的路径长度:从根节点到每一个结点的路径长度之和
结点的带权路径长度:从该节点到树根之间的路径长度与节点上权值的乘积
树的带权路径长度(WPL):树中所有叶子节点的带权路径长度之和
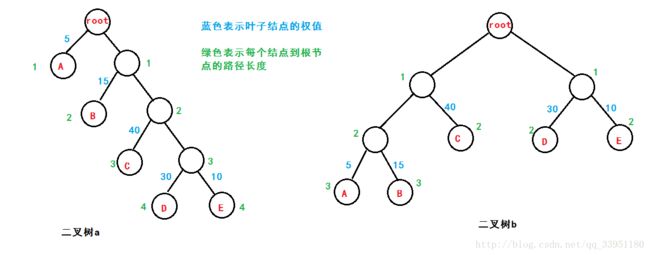
分析上图中的两棵树:
(a)树的路径长度 = 1+1+2+2+3+3+4+4 = 20
WPL = 5*1 + 15*2 + 40*3 + 30*4 + 10*4 = 315
(b)树的路径长度 = 1+1+2+2+2+2+3+3 = 16
WPL = 5*3 + 15*3 + 40*2 + 30*2 + 10*2 = 220
通过比较我们发现,二叉树a的路径长度和WPL值都大于二叉树b,而且上边也给出了哈夫曼树概念,因此在这里二叉树b其实就是一棵哈夫曼树。那么我们如何才能构造这样一棵树呢?!
二、哈夫曼树的构造
其实哈夫曼最早给出了构建树的算法,称为哈夫曼算法,这个算法大家在网上搜搜也就出来了,因此我在这里就不再写了。但是,我相信很多人看了这个都会很蒙圈,所以我就利用图+文字的形式来构建一棵哈夫曼树。
我们在构建这棵哈夫曼树时可利用"贪心算法"的思想来构建,也就是说,每次只考虑局部最优解
(1)先将所有的权值按照从小到大的顺序进行排序,例如为n1,n2,n3,n4,n5,......
(2)每次选出头两个最小权值的结点n1,n2来构建n1和n2的父亲节点N1,其做法是:n1与n2的权值相加作为N1的权值,并且n1和n2中权值较小的作为左孩子
(3)用得到的N1替换n1与n2,可得到N1,n3,n4,n5,.....,每次都要保持从小到大的顺序
(4)重复步骤(2)(3),当所有结点都在树中时,这棵树也就构建好了
需要说的一点是,当在进行步骤(2)(3)时,若遇到两个数的和正好是下一步的两个最小数的其中一个时,则这棵树就继续向上生长;若是两个数的和比较大不是下一步的两个最小数中的一个,就并列生长。
例如:我们利用{0,1,2,3,4,5,6,7,8,9}这组数来构建哈夫曼树
三、哈夫曼编码
哈夫曼研究这种最优二叉树的更大目的是为了解决当年远距离通信的数据传输的最优化问题,其实哈夫曼树最经典的一种应用就是哈夫曼编码,现在我们可以利用哈夫曼编码来进行文件压缩。
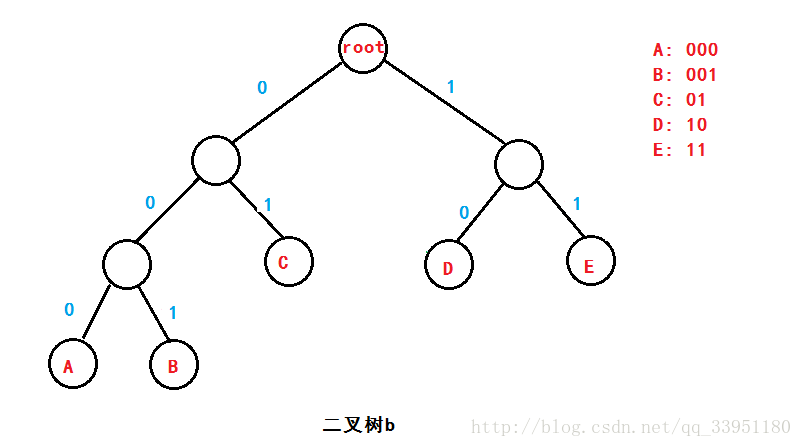
哈夫曼编码:假若我们规定给每个结点的左路标记'0',右路标记'1',那么我们就可以用0、1来表示每个字母。以第一幅图中的二叉树b为例
四、文件压缩
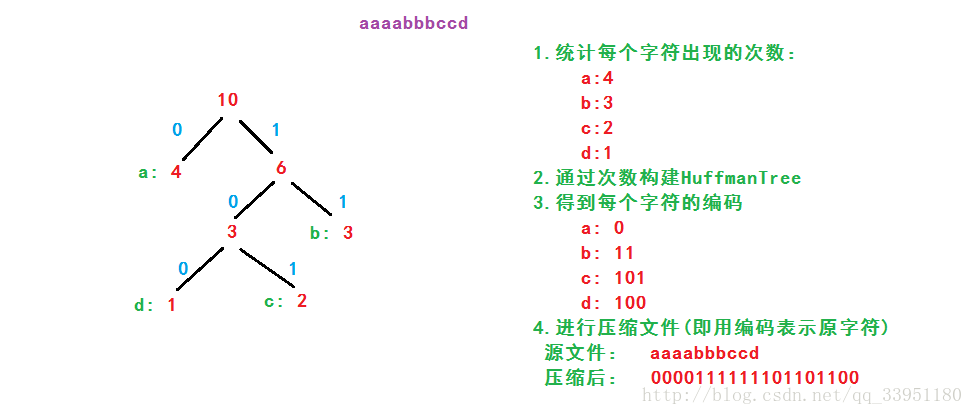
文件压缩的主要思想是利用哈夫曼编码来实现的,但是得到编码之前我们需要构建这棵树。那么利用什么来构建树呢?!这里,我们需要统计每个字符出现的次数,用次数来构建HuffmanTree。假设我们现在有一个.txt的小文件,内容是"aaaabbbccd"。字符存在计算机中时以字节为单位的,因此我们需要将这些字符压缩成0、1表示的编码,0和1表示字节中的“位”,这样能大大降低文件的大小。
上图中的文字就是文件压缩的4个步骤。
对第4步的结果进行对比可以看出,源文件需要的大小是10个字节,压缩后的文件是使用了19个比特位的空间,其实也就是3个字节的大小,剩下不够的5个比特位用0来补。这样其实也就时文件压缩后的效果!
五、文件解压
文件解压时就需要从根节点向叶子节点走了,读取压缩文件的编码,遇到'0'就向树的左边走,遇到'1'就向树的右边走。由于这些字符肯定都是存在与叶子结点上的,因此当遇到叶子节点以后就说明已经还原出一个字符,这时将还原的一个字符写入解压文件中;解压完一个字符后再次开始从根节点向下遍历。
解压文件时会遇到的问题:
上边说过,压缩以后的文件如果不够一个字节大小,会用0来代替空缺的比特位,这样带来的问题就是可能会多解压出字符。以上述的"aaaabbbccd"为例,压缩以后的编码为19比特位:00001111 11110110 100,计算机存储的最小单位为字节,因此这些编码会被存储为00001111 11110110 10000000,后边的五个0对我们来说就是多余的,如果不处理,就会多还原出5个a
解决:
给出一个charCount来统计所有字符串的个数,其实也就是根节点的值,每次还原出一个字符后,charCount就-1,直到charCount为0时说明所有字符都已经解压完成。
PS:以上所有代码我都上传至github,可以点这个链接查看源代码:
https://github.com/lybb/FileCompress
六、测试用例
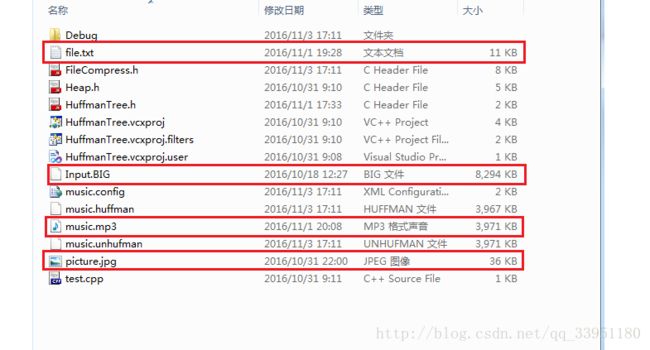
我分别测试了.txt文件、.mp3文件、.jpg文件,还有一个自己定义的.BIG的文件
以Input.BIG文件压缩为例,其进行压缩与解压后的结果如下:
我们不能仅用解压文件与源文件的大小来判断是否解压成功,可以借助BeyondCompared软件来比对,对比结果如下(页面中没有显示红色的字体就表示文件一样):