【总结】FWT算法

前言：

作为FFT又一个衍生算法，FWT相对（NTT）来说比较特殊，特殊在它的运算全部是逻辑运算（即与，或，异或等），这也导致FWT的代码看上去和FFT并不类似，但总的来说FWT是一个相对容易的算法（只不过需要背一些东西）。

---

算法介绍

FFT算法，是用于优化卷积，而FWT是用于优化逻辑运算卷积。形如下图：
$$C[x\oplus y]=\sum A[x]B[y]$$
它同样可以写作
$$C[y]=\sum A[x]B[x\oplus y]$$
而沃尔什变换与FFT最大的区别在于，它没有基于类似单位复根的优化方式，所有优化都是根据不同的运算而构造出来的，也就意味着：
对于与，或，异或，甚至其它的逻辑运算，都有不同的构造方式（所以只能靠背啊！）
另外，FWT同样也是基于分治的优化，但不同于FFT，它的拆分方式非常简单：将原串拆分为大小相等的前后两部分，这也决定了FWT算法仍然需要将数列长度补足到2的整次幂
下面简述一下异或的FWT算法：
GJY大佬ORZ
首先定义正变换：
$$FWT(A)=\{\begin{array}{l}FWT(A_0+A_1,A_0-A_1)\\ \\ A（|A|=1）\end{array}$$
这里的A是我们要进行正变换的数列，$A_0和A_1$分别指A的前半部分和后半部分。
方便起见，我们再定义
$A\oplus B=(\sum A_j{B}_{0\oplus j}，\sum A_j{B}_{1\oplus j}，\sum A_j{B}_{2\oplus j}\dots \dots \sum A_j{B}_{2^n\oplus j})(0\le j\le 2^n)$
现在我们只要证明$FWT(A\oplus B)=FWT(A)\ast FWT(B)$

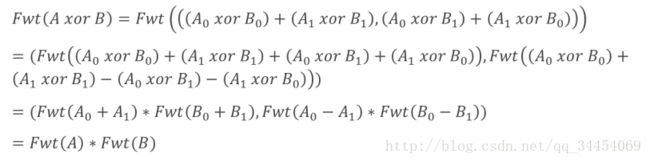
然后就可以进行逆变换，以得到我们需要的结果，对于FWT而言，通过正变换是很容易推出逆变换的：
正变换：$$FWT(A)=FWT(A_0+A_1,A_0-A_1)$$
其逆变换也就是将这个值还原（即小学数学的差和问题）
即：$$iFWT(A)=iFWT(\frac{A_0+A_1}{2},\frac{A_0-A_1}{2})$$
所以代码也超级好写

void FWT(int a[],int n){
    for(int d=1;d<n;d<<=1)
        for(int m=d<<1,i=0;i<n;i+=m)
            for(int j=0;j<d;j++){
                long long x=a[i+j],y=a[i+j+d];
                a[i+j]=(x+y)%MOD;
                a[i+j+d]=(x-y+MOD)%MOD;
            }
}
void IFWT(int a[],int n){
    for(int d=1;d<n;d<<=1)
        for(int m=d<<1,i=0;i<n;i+=m)
            for(int j=0;j<d;j++){
                long long x=a[i+j],y=a[i+j+d];
                a[i+j]=(x+y)%MOD;
                a[i+j+d]=(x-y+MOD)%MOD;
                a[i+j]=(ll)a[i+j]*inv%MOD;
                a[i+j+d]=(ll)a[i+j+d]*inv%MOD;
            }
}

再给出其他几个常见的逻辑运算的正变换：
与：$FWT(A)=FWT(A_0+A_1{A}_1)$
或：$FWT(A)=FWT(A_0,A_0+A_1)$

模板题51nod1773
非常板的模板题，题目要求$calc(u,v)=1$，其实很容易发现，
这无非就是令u在二进制下：
某一个为0的位变为1，或令某一个为1的位变为0，这样就很显然了，
我们令b数列表示在2的整次幂时为1，其余为0的数列
$a[x\oplus y]=a[x]b[y]$
套一个快速幂就可以过了，但注意需要读入输出优化

#include
#include
#include
#include
#define SF scanf
#define PF printf
#define MAXN (1<<20)
#define MOD 1000000007
typedef long long ll;
using namespace std;
int a[MAXN],b[MAXN],res[MAXN];
int n,t;
char out[20];
const long long inv=500000004;
void Read(int &x){
    x=0;
    char c;
    while(c=getchar(),c!=EOF&&(c<'0'||c>'9'));
    x=c-'0';
    while(c=getchar(),c!=EOF&&c>='0'&&c<='9')
        x=x*10+c-'0';
}
void Put(int x){
    int num=0;
    while(x){
        out[++num]=x%10+'0';
        x/=10;
    }
    while(num)
        putchar(out[num--]);
    putchar(' ');
}
void FWT(int a[],int n){
    for(int d=1;d<n;d<<=1)
        for(int m=d<<1,i=0;i<n;i+=m)
            for(int j=0;j<d;j++){
                long long x=a[i+j],y=a[i+j+d];
                a[i+j]=(x+y)%MOD;
                a[i+j+d]=(x-y+MOD)%MOD;
            }
}
void IFWT(int a[],int n){
    for(int d=1;d<n;d<<=1)
        for(int m=d<<1,i=0;i<n;i+=m)
            for(int j=0;j<d;j++){
                long long x=a[i+j],y=a[i+j+d];
                a[i+j]=(x+y)%MOD;
                a[i+j+d]=(x-y+MOD)%MOD;
                a[i+j]=(ll)a[i+j]*inv%MOD;
                a[i+j+d]=(ll)a[i+j+d]*inv%MOD;
            }
}
void fsp(int k){
    for(int i=0;i<n;i++)
        res[i]=b[i];
    while(k){
        if(k&1)
            for(int i=0;i<n;i++)
                res[i]=(ll)res[i]*b[i]%MOD;
        k>>=1;
        for(int i=0;i<n;i++)
            b[i]=(ll)b[i]*b[i]%MOD;
    }
    for(int i=0;i<n;i++)
        b[i]=res[i];
}
int main(){
    SF("%d%d",&n,&t);
    t--;
    n=(1<<n);
    for(int i=0;i<n;i++)
        Read(a[i]);
    for(int i=1;i<n;i<<=1)
        b[i]=1;
    b[0]=1;
    FWT(a,n);
    FWT(b,n);
    fsp(t);
    for(int i=0;i<n;i++)
        a[i]=(ll)a[i]*b[i]%MOD;
    IFWT(a,n);
    for(int i=0;i<n;i++)
        Put(a[i]);
}

另外一道也比较模板的题BZOJ4589
虽然还是一道很简单的模板题，但毕竟和SG定理套在一起了，也算是FWT的优化运算的体现吧。

SG定理告诉我们，每个状态的值为其不能转移到的最小的状态的值，在这道题中，每个堆都能一次拿完，所以每个堆在SG函数中的值就是它本身。

我们只需要知道所有不大于m的质数中异或和为0的方案数即可。
经过简单的思考，很容易发现这还是一道快速幂

令数列中下标为质数的位置值为1，其余为0
我们每次将数列正变换后相乘，得到的数列满足：下标即为这两个数的异或和，值即为方案数，所以要求n个数的异或和只需要取n次幂就可以了。

#include
#include
#include
#include
#include
#include
#define SF scanf
#define PF printf
#define MAXN 100010
#define MOD 1000000007
#define INV 500000004
using namespace std;
typedef long long ll;
void fwt(long long a[],int n){
    for(int d=1;d<n;d<<=1)
        for(int m=d<<1,i=0;i<n;i+=m)
            for(int j=0;j<d;j++){
                long long x=a[i+j],y=a[i+j+d];
                a[i+j]=(x+y)%MOD;
                a[i+j+d]=(x-y+MOD)%MOD;
            }
}
void ifwt(long long a[],int n){
    for(int d=1;d<n;d<<=1)
        for(int m=d<<1,i=0;i<n;i+=m)
            for(int j=0;j<d;j++){
                long long x=a[i+j],y=a[i+j+d];
                a[i+j]=(x+y)*INV%MOD;
                a[i+j+d]=(x-y+MOD)*INV%MOD;
            }
}
bool isprime[MAXN];
int primes[MAXN],cnt;
void prepare(){
    isprime[1]=isprime[0]=1;
    for(int i=2;i<=50000;i++){
        if(isprime[i]==0)
            primes[++cnt]=i;
        for(int j=1;j<=cnt&&i*primes[j]<=50000;j++){
            isprime[i*primes[j]]=1;
            if(i%primes[j]==0)
                break;
        }
    }
}
int fsp(long long x,int y){
    long long res=1;
    while(y){
        if(y&1)
            res=res*x%MOD;
        x=x*x%MOD;
        y>>=1;
    }
    return res;
}
long long a[MAXN];
int main(){
    int n,m;
    prepare();
    while(SF("%d%d",&n,&m)!=EOF){
        int len=1;
        while(len<=m)
            len<<=1;
        for(int i=0;i<len;i++){
            a[i]=(1-isprime[i]);
            if(i>m)
                a[i]=0;
        }
        fwt(a,len);
        for(int i=0;i<len;i++)
            a[i]=fsp(a[i],n);
        ifwt(a,len);
        PF("%lld\n",a[0]);
    }
}