计算机原理之反馈与触发器

目录

 

一、振荡器

二、反馈与触发器

三、R-S触发器

三、电平触发的D型触发器

四、八位锁存器

五、将八位锁存器添加到八位加法器

六、边沿触发器

七、分频器

八、8位行波计数器

九、使用计数器计数

---

 

一、振荡器

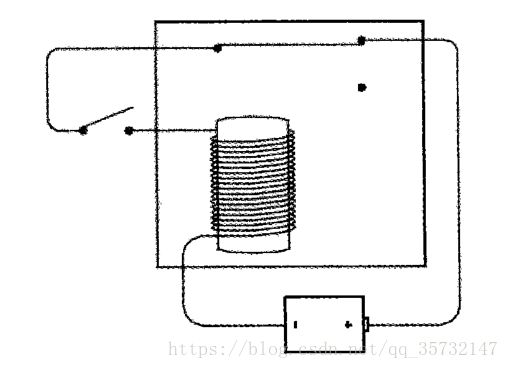
    当开关闭合时，连通的电路使得电磁铁把金属簧片拉了下来，电路不再连通，电磁铁不再具有磁性，金属簧片又弹回原位，电路又一次连通，不断循环这个过程，金属簧片将上下不停来回摆动。

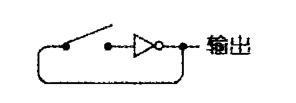
    上面的电路可以简化为：

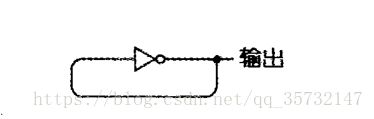
    可以直接把开关省去，这样反向器就会连续地工作：

    这种电路称为振荡器。

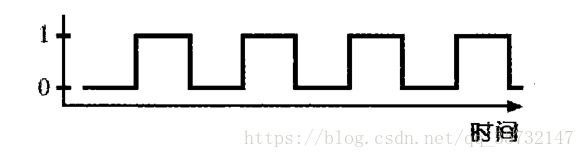
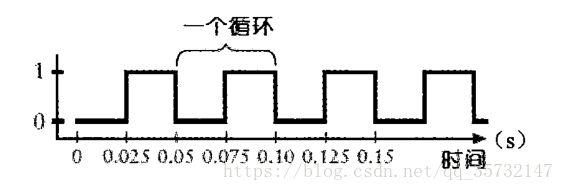
    可以通过下面这幅图充分地了解电路的输出，水平坐标代表时间，垂直坐标表述输出是0还是1：

    振荡器的输出在0和1之间有规律地交替变化（现实中，输出是0的时间应该会比输出是1的时间长一些），所以，振荡器又经常被称为时钟。

    一个循环所占用的时间就是该振荡器的周期：

二、反馈与触发器

    上面的电路称为反馈。

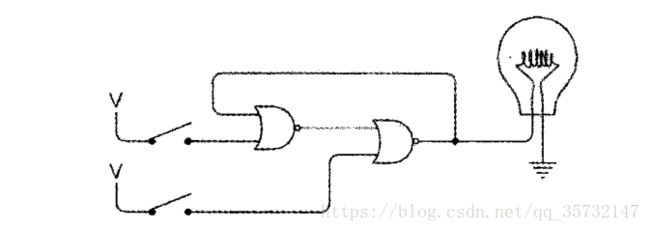
    上面的电路使用了两个或非门，或非门的特点是只有两个输入端都没有电压时，输出端才产生电压：

    所以反馈电路将呈现如下特性：

• 接通上面的开关，灯泡被点亮，断开此开关灯泡仍然亮着。
• 接通下面的开关，灯泡被熄灭，断开此开关灯泡仍然不亮。

    当两个开关都断开时，电路有两个稳定态，这类电路统称为触发器。

    触发器可以记住最近一次是哪个开关先闭合。

三、R-S触发器

    触发器种类繁多，先前所讲述的是最简单的一种R-S（Reset-Set，复位/置位）触发器。

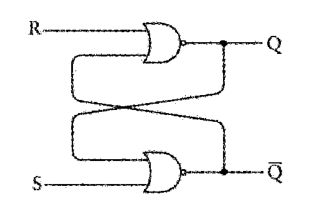
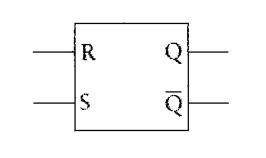
    通常，把上面的电路绘制成下面的形式：

    通常，用Q表示用于点亮灯泡的输出状态，另一个是对Q的取反。

    输入端S（Set）用来置位（把Q设为1），R（Reset）用来复位（把Q设为0）。

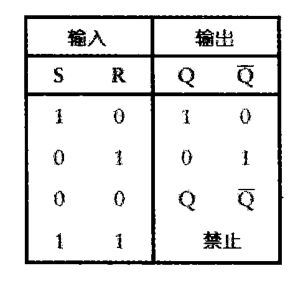
    电路的逻辑表为:

    当S、R状态同时为1时，Q和均会为零，这与Q和互反的假设相矛盾，所以将这种情况禁止。

    R-S触发器可以简化为如下：

三、电平触发的D型触发器

    R-S触发器最突出的特点在于，它可以记住哪个输入端的最终状态为1。

    但有时候需要一种记忆能力更强大的电路，能记住在某个特定时间点上的一个信号是0还是1。（即需要能够自由控制它何时记住信号）

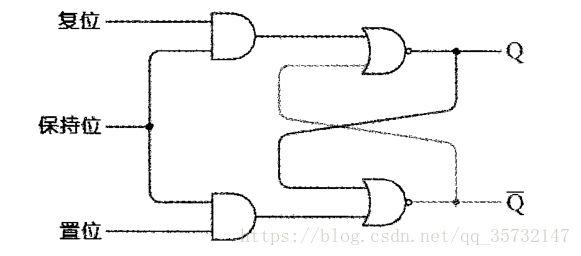
    在R-S触发器的输入端增加两个与门：

    在R-S触发器的逻辑表中：

• 两个输入端同时为1是被禁止的
• 两个输入端同时为0是无意义的，因为那种情况下输出就会保持不变。现在只要将保持位设置为0，就可以实现相同的功能。

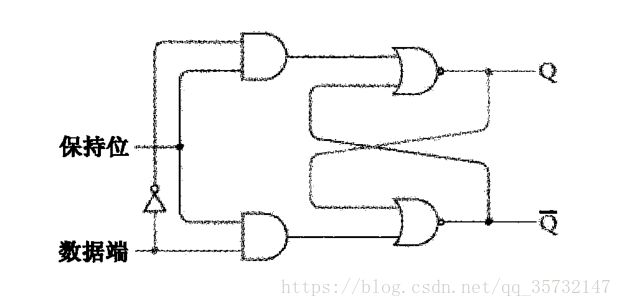
   所以，再给上面的电路加一个反向器，可以得到下面的电路：

    这个电路称为电平触发的D型触发器，D（Data）表示数据端输入。

    所谓电平触发是指当保持位输入为某一特定电平（本例中为“1”）时，触发器才保持数据端的输入值。

    保持位可以标记为时钟（clock），因为它具有类似时钟的属性，可以在0和1之间有规律地来回变化，但现在时钟仅仅用来指示什么时候保存数据。

    电平触发的D型触发器的逻辑表如下：

    这个电路也称为电平触发的D型锁存器，它表示电路锁存住一位数据并保持它，以便将来使用。

    所以这个电路也可以被称为1位存储器。

四、八位锁存器

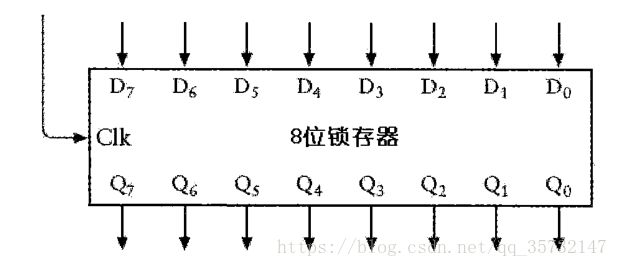
    在一个小盒子里布置8个锁存器，每个锁存器包括两个或非门、两个与门以及一个反向器。

    所有时钟输入端都互相连在一起，如下图所示：

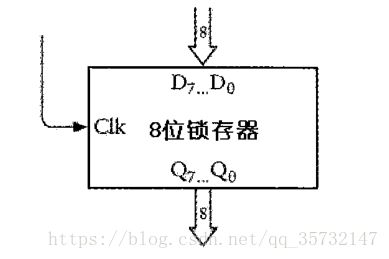
    这个锁存器可以一次保存8位数。

    当时钟信号为1时，D端输入的8位值被送到Q端输出。

    当时钟信号为0时，这8位值将保持不变，直到时钟信号再次被置1。

    可以将8位锁存器简化如下：

五、将八位锁存器添加到八位加法器

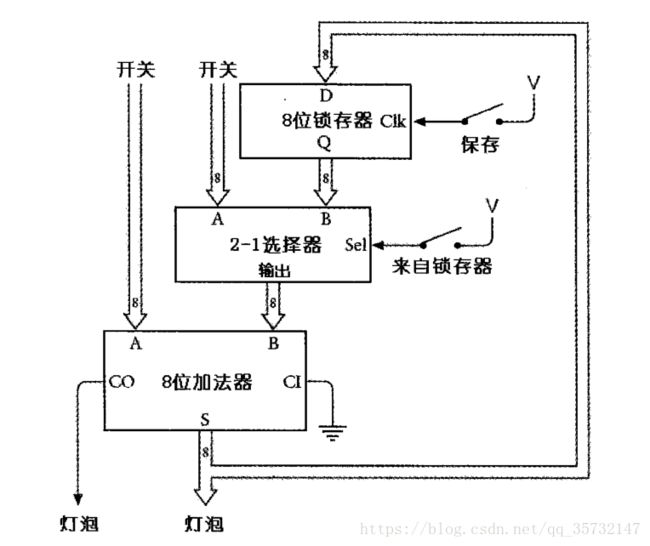
    经过改进，8位加法器的8个S输出端既与灯泡相连，又连接到8位锁存器的数据（D）输入端：

    标记为“保存”的开关是锁存器的时钟输入，用来存放加法器的运算结果。

    标记为2-1选择器的方块是用一个开关来选择加法器的B端输入是取自第2排开关还是取自锁存器的Q端输出。

    2-1选择器使用了8个如下所示的电路：

    如果选择器输入是1，那么或门的输出和B端的输入就是一致的；如果选择端的输入是0，那么或门的输出则和A端输入一致。

    总结起来如下表所示：

    改进后的加法器不能很好地处理进位输出（CO）信号。

    如果两个数的相加使得进位输出信号为1，那么当下个数被加进来的时候，这个信号将被忽略掉。

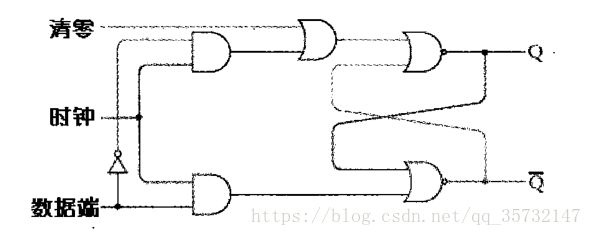
    可以对D触发器做一些修改，为它加入一个或门和一个称为清零（Clear）的输入信号：

    清零信号通常为0，但当它为1时，Q输出为0。

    可以将加法器和存储器的电路改进为如下所示：

    当需要加上一长串数字时，首先按下清零开关，这个操作会使锁存器的输出为0，并且熄灭了所有的灯泡，同时使8位加法器的第2行输入全为0。

六、边沿触发器

    对于某些应用而言，电平触发时钟输入已经足够用了，但是对另外一些应用来说，边沿触发时钟输入则更有效。

    对于边沿触发器而言，只有当时钟从0跳变到1时，才会引起输出的改变。    

    边沿触发器与电平触发的D型触发器的区别在于：

    在电平触发器中，当时钟输入为0时，数据端输入的任何改变都不会影响输出；而在边沿触发器中，当时钟输入为1时，数据端输入的改变也不会影响输出。边沿触发器只有在时钟输入从0变到1的瞬间，数据端的输入才会影响边沿触发器的输出。

    边沿触发的D型触发器是由两级R-S触发器按如下方式连接而成：

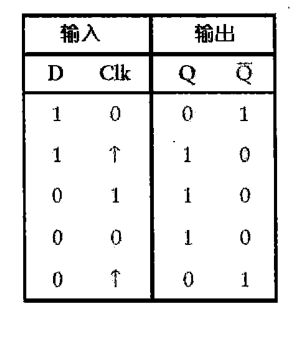
    边沿触发的D型触发器的逻辑表如下：

    箭头表示从0到1的瞬时变化。

    这里的原理是： 

        一个R-S触发器有通过调整时钟随时记录D端数据的变化的功能。

        而将两个R-S触发器叠加在一起，通过同一个时钟同时控制这两个R-S触发器，就产生了第二级R-S触发器的D端只能在某一个特定的瞬间变化的功能，而这个特定瞬间可以适当地调整为时钟从0到1变化的瞬间。

    由此可以总结出：

• 使用一个R-S触发器具有通过调整时钟随时记录D端数据的变化的功能
• 使用两个R-S触发器只有在某个瞬间记录D端数据变化的功能

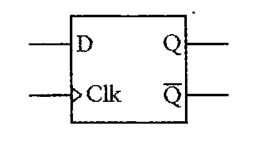
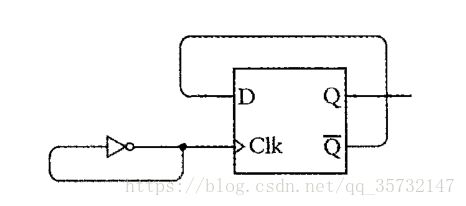
    边沿触发的D型触发器的简写符号如下：

    图中的小三角符号表示触发器是边沿触发的。

七、分频器

    把振荡器的输出与边沿触发的D型触发器的时钟端输入连接，同时把端输出连接到本身的D输入端：

    电路启动时，假设时钟输入为0且Q输出也为0，则端输出为1，而是和D端输入相连的。

    接下来电路的逻辑变化是这样的：

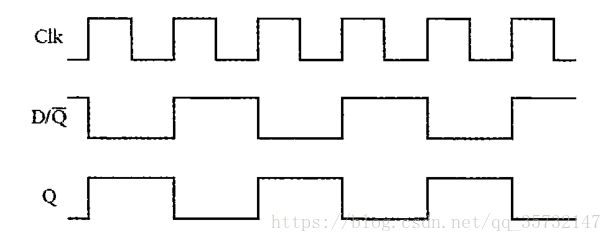
    下面的时序图能更加清楚地说明逻辑变化:

    如果这个振荡器的频率是20Hz（即20个周期的时间为1s），那么Q的输出频率是它的一半，即10Hz。

    由于这个原因，这种电路称为分频器。

    分频器的输出可以作为另一个分频器的Clk输入，并再一次进行分频：

    在信号变化的时序图中标上0和1：

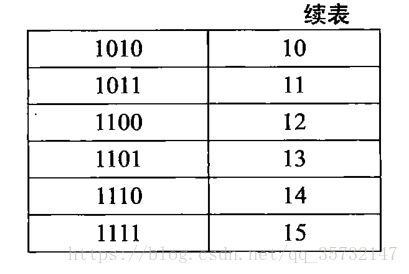
    将这个图顺时针旋转90°，可以发现每一行的4位数字分别对应了十进制中的0~15中的一个数：

    在每一次时钟信号的正跳变时，计数器的输出是增加的，即递增1。

八、8位行波计数器

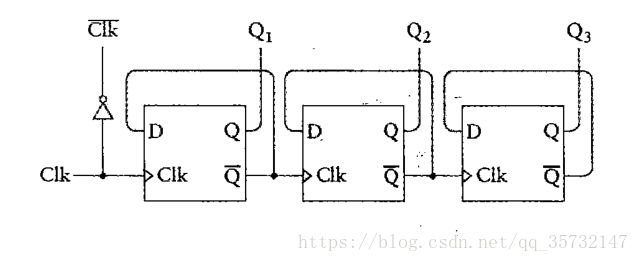
    把8个触发器连接在一起，然后放入一个盒子中，构成了一个8位计数器。

    这个计数器称为“8位行波计数器”，因为每一个触发器的输出都是下一个触发器的时钟输入。

    变化是在触发器中一级一级地顺序传递的，最后一级触发器的变化必定会有一些延迟。

    时钟信号的每一个正跳变发生时，一些Q输出可能会改变，而另外一些可能不变，但总体上来说它们所表示的二进制编码递增了1。

九、使用计数器计数

    如果把一个振荡器连接到8位行波计数器的时钟输入端上，那么这个计数器会显示出振荡器经过的循环次数。

    当计数器总数达到11111111（十进制的255），它又返回为00000000。

    使用计数器确定振荡器频率的最简单的方法就是把计数器的8个输出端分别接到8只灯泡上。

    当所有的输出都是0时（即所有灯泡都是熄灭的），启动一个秒表计时；当所有灯泡都点亮时，停止秒表计时。

    这就是振荡器循环256次所需要的时间。

    假设这个时间为10s，则振荡器的频率是256 / 10， 即25.6Hz。