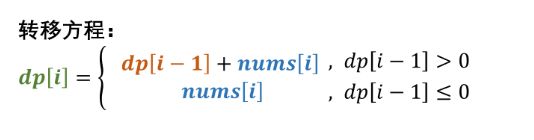二刷剑指offer 22-40
面试题39. 数组中出现次数超过一半的数字

核心理念为 “正负抵消” ;时间和空间复杂度分别为 O(N) 和 O(1);是本题的最佳解法。
class Solution {
public int majorityElement(int[] nums) {
//摩尔投票
int count = 0;
Integer card = null;
for(int num:nums){
if(count == 0)
card = num;
count += (card == num)?1:-1;
}
return card;
}
}
哈希表统计法:遍历数组 nums,用 HashMap 统计各数字的数量,最终超过数组长度一半的数字则为众数。此方法时间和空间复杂度均为 O(N)。
//HashMap方法:不是双百解法,但是容易理解,且普适性强,并考虑了数组中不存在满足条件的众数和数组为空的情况
public int majorityElement(int[] nums) {
HashMap<Integer,Integer> map = new HashMap<>();
int length = nums.length/2;
for(int i=0;i<nums.length;i++){
if(map.containsKey(nums[i])) {
//这里不能直接map.get(nums[i])++;
map.put(nums[i],map.get(nums[i])+1);
}else{
map.put(nums[i],1);
}
//注意:这里if不能放在第一个if中,否则会在数组长度为1时出错,无法返回正确的nums[i]的值
//这里i>=length,之所以带等号,也是为了满足长度为1的情况,因为i从0开始
//按照题目要求,必须众数次数超过长度的一半,则有第一个判断条件,相当于剪枝,当然下面的第一个判断条件也可以不加
if(i>=length&&map.get(nums[i])>length) return nums[i];
}
return 0;//当不存在满足要求的数字或者数组长度为0时
}
需要的数字出现次数多于一半 那么排序后必定在中间 排序解法O(nlogn)
面试题40. 最小的k个数
用快排最最最高效解决 TopK 问题:O(N)。直接通过快排切分排好第 K 小的数(下标为 K-1),那么它左边的数就是比它小的另外 K-1 个数啦~
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
quickselect(arr, 0, arr.length - 1, k);
return Arrays.copyOfRange(arr, 0, k);
}
private void quickselect(int[] nums, int start, int end, int k) {
while (start < end) {
// 这边做了了小优化,三数取中~前两步先确定最后一个一定是最大的,然后只要把中间那个数放第一个位置即可
// 如果你嫌麻烦可以直接 int pivot = nums[start];
int mid = start + (end - start) / 2;
if (nums[start] > nums[end]) swap(nums, start, end);
if (nums[mid] > nums[end]) swap(nums, mid, end);
if (nums[mid] > nums[start]) swap(nums, mid, start);
int pivot = nums[start];
int i = start, j = end;
while (i <= j) {
//升序~
while (i <= j && nums[i] < pivot) i++;
while (i <= j && nums[j] > pivot) j--;
if (i <= j) {
swap(nums,i,j);
i++;
j--;
}
}
if (i >= k) {
end = i - 1;
} else {
start = i;
}
}
}
private void swap(int[] nums, int a, int b) {
int temp = nums[a];
nums[a] = nums[b];
nums[b] = temp;
}
}
本题是求前 K 小,因此用一个容量为 K 的大根堆,每次 poll 出最大的数,那堆中保留的就是前 K 小啦(注意不是小根堆!小根堆的话需要把全部的元素都入堆,那是 O(NlogN),就不是 O(NlogK)啦~~)
// 保持堆的大小为K,然后遍历数组中的数字,遍历的时候做如下判断:
// 1. 若目前堆的大小小于K,将当前数字放入堆中。
// 2. 否则判断当前数字与大根堆堆顶元素的大小关系,如果当前数字比大根堆堆顶还大,这个数就直接跳过;
// 反之如果当前数字比大根堆堆顶小,先poll掉堆顶,再将该数字放入堆中。
class Solution {
public int[] getLeastNumbers(int[] arr, int k) {
if (k == 0 || arr.length == 0) {
return new int[0];
}
// 默认是小根堆,实现大根堆需要重写一下比较器。
Queue<Integer> pq = new PriorityQueue<>((v1, v2) -> v2 - v1);
for (int num: arr) {
if (pq.size() < k) {
pq.offer(num);
} else if (num < pq.peek()) {
pq.poll();
pq.offer(num);
}
}
// 返回堆中的元素
int[] res = new int[pq.size()];
int idx = 0;
for(int num: pq) {
res[idx++] = num;
}
return res;
}
}
面试题42. 连续子数组的最大和
class Solution {
public int maxSubArray(int[] nums) {
int result=nums[0];
int sum=0;
for(int i=0;i<nums.length;i++){
sum=sum>0?sum+nums[i]:nums[i];
result=Math.max(sum,result);
}
return result;
}
}
面试题50. 第一个只出现一次的字符

时间复杂度 O(N) : N为字符串 s 的长度;需遍历 s 两轮,使用 O(N) ;HashMap 查找的操作复杂度为 O(1);
空间复杂度 O(N) : HashMap 需存储 N个字符的键值对,使用 O(N)大小的额外空间
class Solution {
public char firstUniqChar(String s) {
HashMap<Character, Boolean> dic = new HashMap<>();
char[] sc = s.toCharArray();
for(char c : sc)
dic.put(c, !dic.containsKey(c));
for(char c : sc)
if(dic.get(c)) return c;
return ' ';
}
}
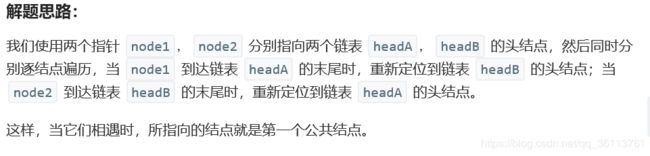
面试题52. 两个链表的第一个公共节点
- 时间复杂度:O(M+N)。
- 空间复杂度:O(1)。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
//思路:双指针法。
ListNode pA = headA, pB = headB;
while(pA != pB){
pA = pA == null ? headB : pA.next;
pB = pB == null ? headA : pB.next;
}
return pA;
}
}
面试题53 - I. 在排序数组中查找数字 I
思路:二分查找
(1) 定义双指针遍历两次数组分别找出等于目标值的开始和结束位置。
(2) 计算出等于目标值的位置区间,就是要求的次数。
class Solution {
public int search(int[] nums, int target) {
if(nums == null || nums.length < 1
|| target < nums[0] || target > nums[nums.length - 1]){
return 0;
}
// 找到升序数组最后一个目标值下一位和第一个目标值位置,差就是目标值个数。
return getLast(nums, target) - getLast(nums, target - 1);
}
int getLast(int[] nums, int target) {
// 定义双指针,初始化指向数组的两端。
int left = 0, right = nums.length - 1;
// 当 left 大于 right 则跳出循环,left 指向为查找位置。
while (left <= right) {
// 找到中间位置。
int mid = left + (right - left) / 2;
// 根据每次中间位置值和目标值比较移动指针。
if (nums[mid] <= target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return left;
}
}
面试题53 - II. 0~n-1中缺失的数字
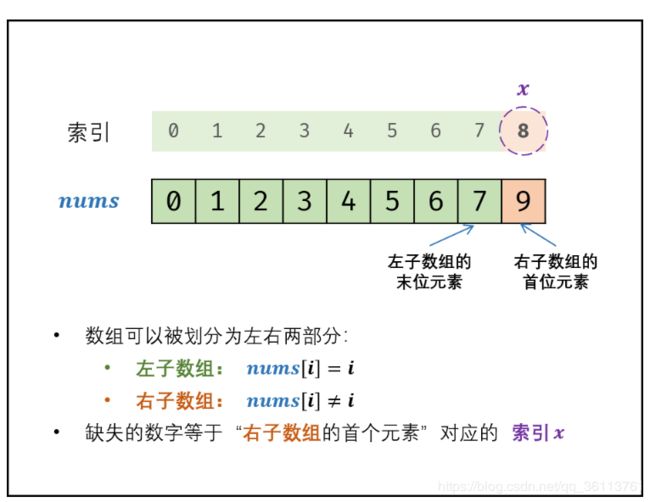
有序就要二分 ,异或只是为了炫技
时间复杂度 O(logN): 二分法为对数级别复杂度。
空间复杂度 O(1): 几个变量使用常数大小的额外空间。
class Solution {
public int missingNumber(int[] nums) {
int i = 0, j = nums.length - 1;
while(i <= j) {
int m = (i + j) / 2;
if(nums[m] == m) i = m + 1;
else j = m - 1;
}
return i;
}
}
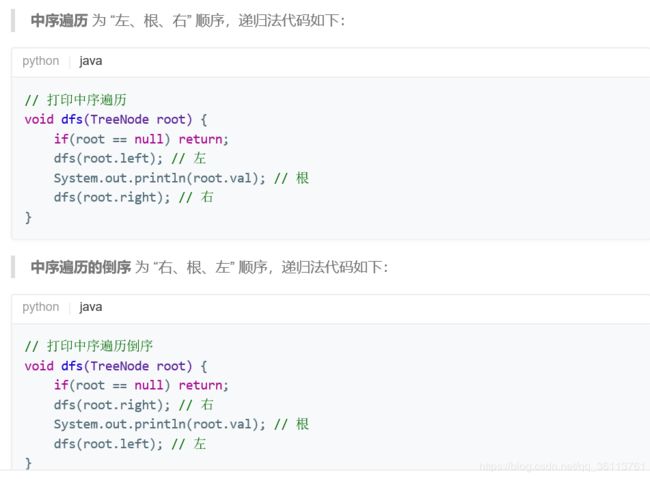
面试题54. 二叉搜索树的第k大节点
二叉搜索树的一个特性:通过中序遍历所得到的序列,就是有序的。二叉搜索树的 中序遍历倒序 为 递减序列
中序遍历 + 提前返回
时间复杂度 O(N) : 当树退化为链表时(全部为右子节点),无论 kkk 的值大小,递归深度都为 N,占用 O(N) 时间。
空间复杂度 O(N) : 当树退化为链表时(全部为右子节点),系统使用 O(N) 大小的栈空间。
class Solution {
int res, k;
public int kthLargest(TreeNode root, int k) {
this.k = k;
dfs(root);
return res;
}
void dfs(TreeNode root) {
if(root == null) return;
dfs(root.right);
if(k == 0) return;
if(--k == 0) res = root.val;
dfs(root.left);
}
}
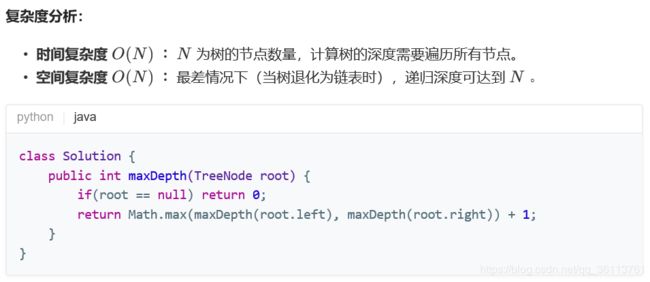
面试题55 - I. 二叉树的深度
面试题55 - II. 平衡二叉树
如果某二叉树中任意节点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。
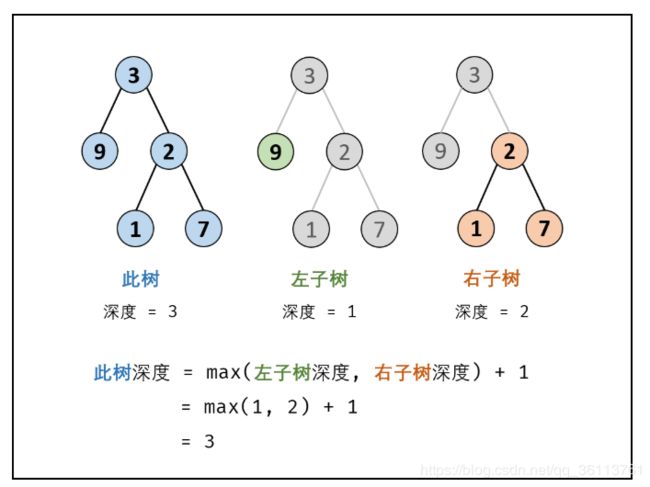

时间复杂度 O(N): N 为树的节点数;最差情况下,需要递归遍历树的所有节点。
空间复杂度 O(N): 最差情况下(树退化为链表时),系统递归需要使用 O(N) 的栈空间。
class Solution {
public boolean isBalanced(TreeNode root) {
return recur(root) != -1;
}
private int recur(TreeNode root) {
if (root == null) return 0;
int left = recur(root.left);
if(left == -1) return -1;
int right = recur(root.right);
if(right == -1) return -1;
return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
}
}
面试题57. 和为s的两个数字
对撞双指针while(i
空间复杂度 O(1): 变量 ii, jj 使用常数大小的额外空间。
class Solution {
public int[] twoSum(int[] nums, int target) {
int i = 0, j = nums.length - 1;
while(i < j) {
int s = nums[i] + nums[j];
if(s < target) i++;
else if(s > target) j--;
else return new int[] { nums[i], nums[j] };
}
return new int[0];
}
}
面试题57 - II. 和为s的连续正数序列
这个算法是这样的:先找出2个连续的和为target的数,再找出连续的3个、4个…怎么找呢?其实是算出来的。这里我每次算出序列中最小的那个数。假设有2个数的和等于target,设最小的那个数的值为n,显然n+(n+1)=target,则n=(target-1)/2;如果没有2个数的和为target,那么假设有3个,则有n+(n+1)+(n+2)=target,n=(target-1-2)/3;以此类推,如果我们用i来表示序列长度(代码中我设置初值为1,方便对target做减法),那么长度为i的序列中最小的那个数n(target-(1+2+3+…+i-1))/i.
还有就是,显然,在和相等的情况下,序列越长它的头部的那个数就越小。由于我们从序列最短的情况开始求,因此最后我们只要把ArrayList倒序复制(其实只是复制了地址)到二维数组中即可。
class Solution {
public int[][] findContinuousSequence(int target) {
List<int[]> result = new ArrayList<>();
int i = 1;
while(target>0)
{
//target -= i;
//i++;
target -= i++;
if(target>0 && target%i == 0)
{
int[] array = new int[i];
for(int k = target/i, j = 0; k < target/i+i; k++,j++)
{
array[j] = k;
}
result.add(array);
}
}
Collections.reverse(result);
return result.toArray(new int[0][]);
}
}
面试题58 - I. 翻转单词顺序
需要注意的是 如果字符串前面有空格 split() 会产生一个 “”
如果中间有连续的三个空格 会产生两个""
另外 String类型 用"=="无效 要使用equals() 方法判断

class Solution {
public String reverseWords(String s) {
String[] a = s.split(" ");
StringBuffer sb = new StringBuffer();
//倒序遍历数组
for(int i = a.length-1;i>=0;i--){
//不是空字符
if(!a[i].equals("")) {
sb.append(a[i]);
sb.append(" ");
}
}
return sb.toString().trim();
}
}
面试题58 - II. 左旋转字符串
时间复杂度 O(N): 线性遍历 s并添加,使用线性时间;
空间复杂度 O(N): 新建的辅助 res使用 O(N)大小的额外空间。
class Solution {
public String reverseLeftWords(String s, int n) {
StringBuilder res = new StringBuilder();
for(int i = n; i < n + s.length(); i++)
//不然就要两个for循环
res.append(s.charAt(i % s.length()));
return res.toString();
}
}
class Solution {
public String reverseLeftWords(String s, int n) {
return s.substring(n, s.length()) + s.substring(0, n);
}
}
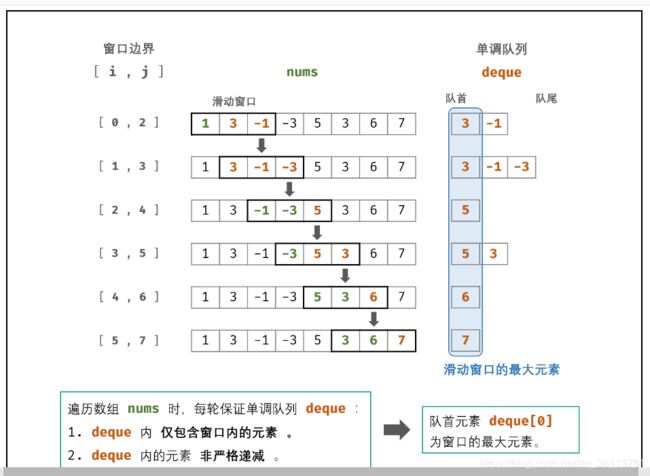
面试题59 - I. 滑动窗口的最大值
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if(nums.length == 0 || k == 0) return new int[0];
Deque<Integer> deque = new LinkedList<>();
int[] res = new int[nums.length - k + 1];
for(int j = 0, i = 1 - k; j < nums.length; i++, j++) {
if(i > 0 && deque.peekFirst() == nums[i - 1])
deque.removeFirst(); // 删除 deque 中对应的 nums[i-1]
while(!deque.isEmpty() && deque.peekLast() < nums[j])
deque.removeLast(); // 保持 deque 递减
deque.addLast(nums[j]);
if(i >= 0)
res[i] = deque.peekFirst(); // 记录窗口最大值
}
return res;
}
}
面试题60. n个骰子的点数
class Solution {
public double[] twoSum(int n) {
//动态规划:设F(n,s)F(n,s)F(n,s)为当骰子数为n,和为s的情况数量。
//当n=1时,F(1,s)=1,其中s=1,2,3,4,5,6
//当n≥2时,F(n,s)=F(n−1,s−1)+F(n−1,s−2)+F(n−1,s−3)+F(n−1,s−4)+F(n−1,s−5)+F(n−1,s−6)
//所以,P(n,s)=F(n,s)/6^n
int [][]dp=new int[n+1][6*n+1];//点数和最大是6*n
//初始化边界条件
for(int s=1;s<=6;s++) dp[1][s]=1;//1个筛子 任何点数都是1种
for(int i=2;i<=n;i++){ //骰子个数
for(int s=i;s<=6*i;s++){ //点数和 有哪些
//求dp[i][s]
for(int d=1;d<=6;d++){ //最后一个骰子 分别投 1 2 3 4 5 6
if(s-d==0)break;//为0了 (s-d==0了)
dp[i][s]+=dp[i-1][s-d];
}
}
}
double total =Math.pow((double)6,(double)n);//总的点数次数是6^n
double[] ans =new double[5*n+1];//点数和大小:从n---到--6*n 遍历
for(int i=n;i<=6*n;i++){
ans[i-n]=dp[n][i]/total;
}
return ans;
}
}
面试题61. 扑克牌中的顺子
从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12,K为13,而大、小王为 0 ,可以看成任意数字。A 不能视为 14。
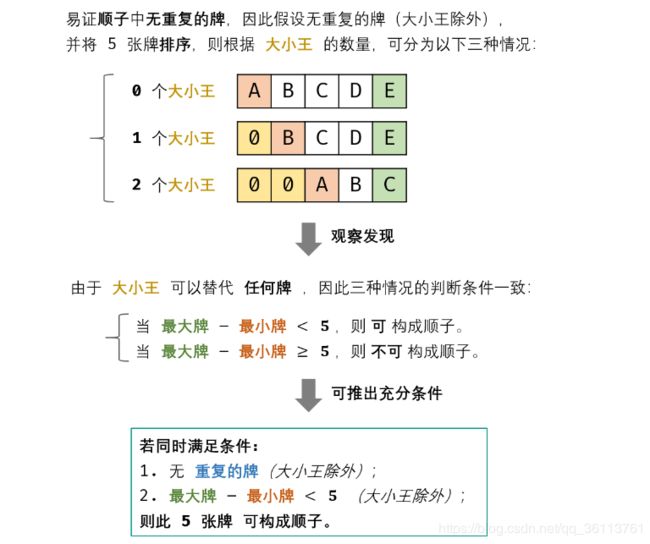
时间复杂度 O(N)=O(5)=O(1) : 其中 NNN 为 nums长度,本题中 N≡5N \equiv 5N≡5 ;遍历数组使用 O(N)时间。
空间复杂度 O(N)=O(5)=O(1): 用于判重的辅助 Set 使用 O(N) 额外空间。
class Solution {
public boolean isStraight(int[] nums) {
Set<Integer> repeat = new HashSet<>();
int max = 0, min = 14;
for(int num : nums) {
if(num == 0) continue; // 跳过大小王
max = Math.max(max, num); // 最大牌
min = Math.min(min, num); // 最小牌
if(repeat.contains(num)) return false; // 若有重复,提前返回 false
repeat.add(num); // 添加此牌至 Set
}
return max - min < 5; // 最大牌 - 最小牌 < 5 则可构成顺子
}
}
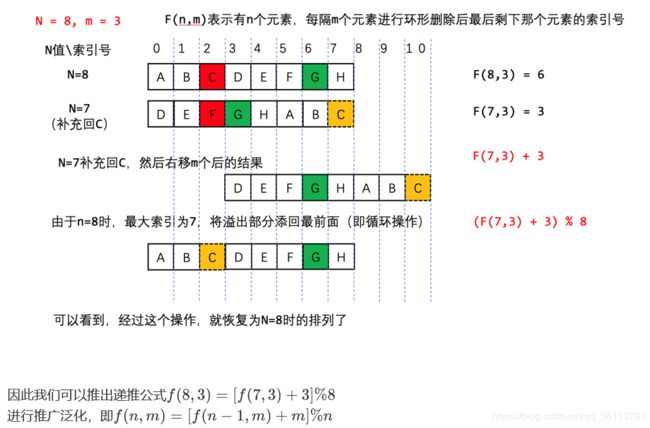
面试题62. 圆圈中最后剩下的数字
class Solution {
public int lastRemaining(int n, int m) {
//最后被删除的那个人的索引一定为零,因为删除一个人之后就会将气候的索引重置
int ans = 0;
// 最后一轮剩下2个人,所以从2开始反推
for (int i = 2; i <= n; i++) {
ans = (ans + m % i)%i;
}
return ans;
}
}
面试题65. 不用加减乘除做加法

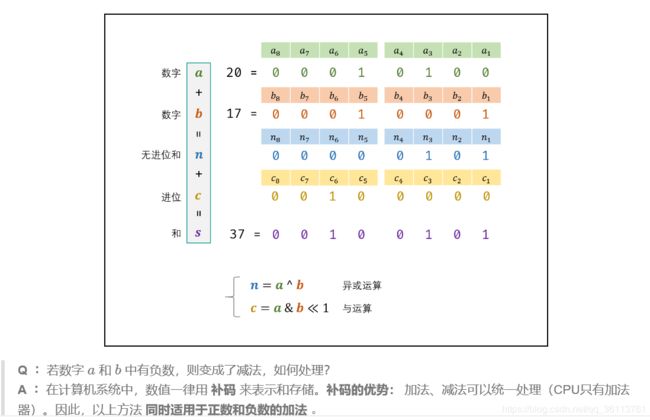
^ 亦或 ----相当于 无进位的求和, 想象10进制下的模拟情况:(如:19+1=20;无进位求和就是10,而非20;因为它不管进位情况)
& 与 ----相当于求每位的进位数, 先看定义:1&1=1;1&0=0;0&0=0;即都为1的时候才为1,正好可以模拟进位数的情况,还是想象10进制下模拟情况:(9+1=10,如果是用&的思路来处理,则9+1得到的进位数为1,而不是10,所以要用<<1向左再移动一位,这样就变为10了);
class Solution {
public int add(int a, int b) {
//a^b是不考虑进位的加法
//a&b<<1是进位
//一直递归,运算&最终会导致进位为0,递归结束
return b == 0 ? a : add(a^b, (a&b)<<1);
}
}
面试题66. 构建乘积数组
class Solution {
public int[] constructArr(int[] a) {
if(a.length == 0) return new int[0];
int[] b = new int[a.length];
b[0] = 1;
int tmp = 1;
for(int i = 1; i < a.length; i++) {
b[i] = b[i - 1] * a[i - 1];
}
for(int i = a.length - 2; i >= 0; i--) {
tmp *= a[i + 1];
b[i] *= tmp;
}
return b;
}
}
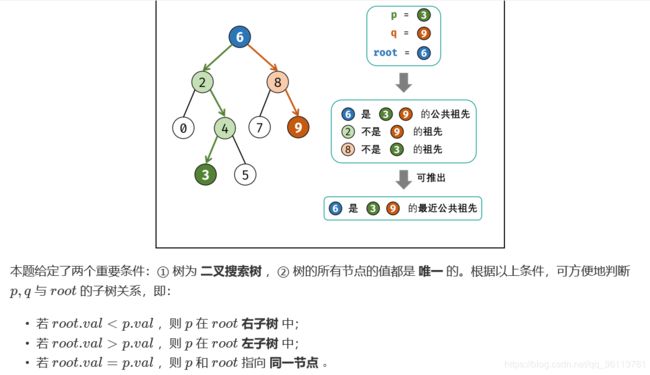
面试题68 - I. 二叉搜索树的最近公共祖先
最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。
所有节点的值都是唯一的。
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
while(root != null) {
if(root.val < p.val && root.val < q.val) // p,q 都在 root 的右子树中
root = root.right; // 遍历至右子节点
else if(root.val > p.val && root.val > q.val) // p,q 都在 root 的左子树中
root = root.left; // 遍历至左子节点
//p,q各在一边,说明当前的根就是最近共同祖先
else break;
}
return root;
}
}
面试题68 - II. 二叉树的最近公共祖先
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q) return root;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if(left == null && right == null) return null; // 1.
if(left == null) return right; // 3.
if(right == null) return left; // 4.
return root; // 2. if(left != null and right != null)
}
}
难度提升到中等
面试题07. 重建二叉树
//利用原理,先序遍历的第一个节点就是根。在中序遍历中通过根 区分哪些是左子树的,哪些是右子树的
//左右子树,递归
HashMap<Integer, Integer> map = new HashMap<>();//标记中序遍历
int[] preorder;//保留的先序遍历
public TreeNode buildTree(int[] preorder, int[] inorder) {
this.preorder = preorder;
for (int i = 0; i < preorder.length; i++) {
map.put(inorder[i], i);
}
return recursive(0,0,inorder.length-1);
}
/**
* @param pre_root_idx 先序遍历的索引
* @param in_left_idx 中序遍历的索引
* @param in_right_idx 中序遍历的索引
*/
public TreeNode recursive(int pre_root_idx, int in_left_idx, int in_right_idx) {
//相等就是自己
if (in_left_idx > in_right_idx) {
return null;
}
//root_idx是在先序里面的
TreeNode root = new TreeNode(preorder[pre_root_idx]);
// 有了先序的,再根据先序的,在中序中获 当前根的索引
int idx = map.get(preorder[pre_root_idx]);
//左子树的根节点就是 左子树的(前序遍历)第一个,就是+1,左边边界就是left,右边边界是中间区分的idx-1
root.left = recursive(pre_root_idx + 1, in_left_idx, idx - 1);
//由根节点在中序遍历的idx 区分成2段,idx 就是根
//右子树的根,就是右子树(前序遍历)的第一个,就是当前根节点 加上左子树的数量
// pre_root_idx 当前的根 左子树的长度 = 左子树的左边-右边 (idx-1 - in_left_idx +1) 。最后+1就是右子树的根了
root.right = recursive(pre_root_idx + (idx-1 - in_left_idx +1) + 1, idx + 1, in_right_idx);
return root;
}
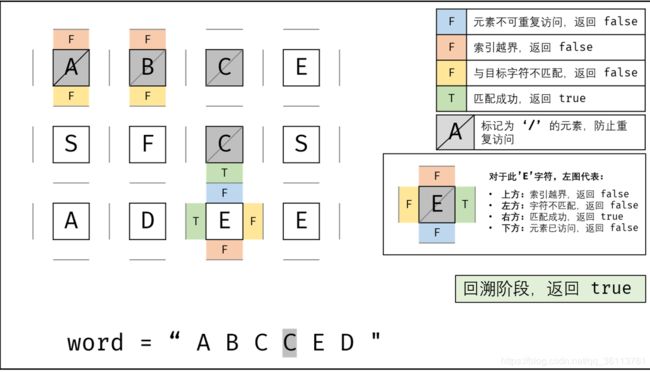
面试题12. 矩阵中的路径
下上右左
class Solution {
public boolean exist(char[][] board, String word) {
char[] words = word.toCharArray();
for(int i = 0; i < board.length; i++) {
for(int j = 0; j < board[0].length; j++) {
if(dfs(board, words, i, j, 0)) return true;
}
}
return false;
}
boolean dfs(char[][] board, char[] word, int i, int j, int k) {
if(i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != word[k]) return false;
if(k == word.length - 1) return true;
char tmp = board[i][j];
board[i][j] = '/';
boolean res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) ||
dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i , j - 1, k + 1);
board[i][j] = tmp;
return res;
}
}
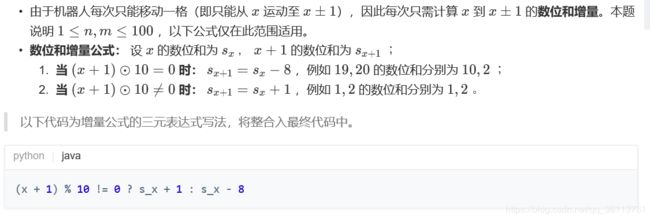
面试题13. 机器人的运动范围
class Solution {
int m, n, k;
boolean[][] visited;
public int movingCount(int m, int n, int k) {
this.m = m; this.n = n; this.k = k;
this.visited = new boolean[m][n];
return dfs(0, 0, 0, 0);
}
public int dfs(int i, int j, int si, int sj) {
if(i >= m || j >= n || k < si + sj || visited[i][j]) return 0;
visited[i][j] = true;
return 1 + dfs(i + 1, j, (i + 1) % 10 != 0 ? si + 1 : si - 8, sj) + dfs(i, j + 1, si, (j + 1) % 10 != 0 ? sj + 1 : sj - 8);
}
}
面试题14- I. 剪绳子
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。




class Solution {
public int cuttingRope(int n) {
if(n<=3) return n-1;
int res=1;
while(n>4){
res*=3;
n-=3;
}
return res*n;
}
}
面试题14- II. 剪绳子 II
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m] 。请问 k[0]k[1]…k[m] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
此题与14-I也就是上一题的区别在于此题n的范围变大,可能会造成大数越界的情况,用寻常的dp很可能会超时或出错,故使用贪心思想解决,剪绳子数学问题其实就是尽可能多地切3的片段,我们可以以n>4来作为循环跳出点。
循环结束的结果分为三种:
1.n=2,等于说无限除以3,最后余下绳子长度为2,此时将res乘以2即可
2.n=3,绳子全部用完,直接所有3相乘即可
3.n=4,等于说余下绳子长度为1,因为4%3=1,但是3<22,也就是4本身,故最后乘4
class Solution {
public int cuttingRope(int n) {
if(n<=3) return n-1;
long res=1;
while(n>4){
res*=3;
res=res%1000000007;
n-=3;
}
//这里必须取括号,否则会优先计算res*n的值,报错会超出范围
return (int)(res*n%1000000007);
}
}
面试题16. 数值的整数次方
class Solution {
public double myPow(double x, int n) {
if(x == 0) return 0;
//幂
long b = n;
double res = 1.0;
if(b < 0) {
x = 1 / x;
b = -b;
}
while(b > 0) {
if((b & 1) == 1)
res *= x;
x *= x;
b >>= 1;
}
return res;
}
}
面试题20. 表示数值的字符串
请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串"+100"、“5e2”、"-123"、“3.1416”、“0123"都表示数值,但"12e”、“1a3.14”、“1.2.3”、“±5”、"-1E-16"及"12e+5.4"都不是。
class Solution {
public boolean isNumber(String s) {
if(s == null || s.length() == 0){
return false;
}
//标记是否遇到相应情况
boolean numSeen = false;
boolean dotSeen = false;
boolean eSeen = false;
char[] str = s.trim().toCharArray();
for(int i = 0;i < str.length; i++){
if(str[i] >= '0' && str[i] <= '9'){
numSeen = true;
}else if(str[i] == '.'){
//.之前不能出现.或者e
if(dotSeen || eSeen){
return false;
}
dotSeen = true;
}else if(str[i] == 'e' || str[i] == 'E'){
//e之前不能出现e,必须出现数
if(eSeen || !numSeen){
return false;
}
eSeen = true;
numSeen = false;//重置numSeen,排除123e或者123e+的情况,确保e之后也出现数
}else if(str[i] == '-' || str[i] == '+'){
//+-出现在0位置或者e/E的后面第一个位置才是合法的
if(i != 0 && str[i-1] != 'e' && str[i-1] != 'E'){
return false;
}
}else{//其他不合法字符
return false;
}
}
return numSeen;
}
}
面试题31. 栈的压入、弹出序列
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
Stack<Integer> stack = new Stack<>();
int i = 0;
for(int num : pushed) {
stack.push(num); // num 入栈
while(!stack.isEmpty() && stack.peek() == popped[i]) { // 循环判断与出栈
stack.pop();
i++;
}
}
return stack.isEmpty();
}
}
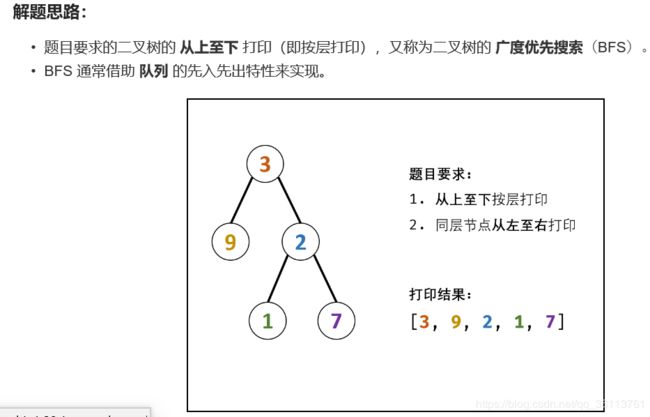
面试题32 - I. 从上到下打印二叉树
class Solution {
public int[] levelOrder(TreeNode root) {
if(root == null) return new int[0];
Queue<TreeNode> queue = new LinkedList<>(){{ add(root); }};
ArrayList<Integer> ans = new ArrayList<>();
while(!queue.isEmpty()) {
TreeNode node = queue.poll();
ans.add(node.val);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
int[] res = new int[ans.size()];
for(int i = 0; i < ans.size(); i++)
res[i] = ans.get(i);
return res;
}
}
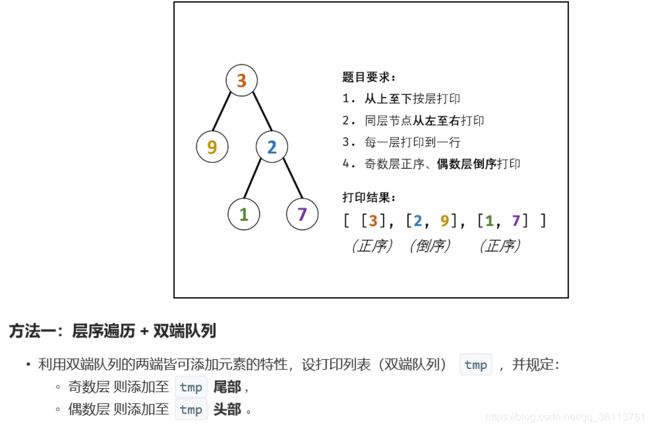
面试题32 - III. 从上到下打印二叉树 III
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
if(root != null) queue.add(root);
while(!queue.isEmpty()) {
LinkedList<Integer> tmp = new LinkedList<>();
for(int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
if(res.size() % 2 == 0) tmp.addLast(node.val); // 偶数层 -> 队列头部
else tmp.addFirst(node.val); // 奇数层 -> 队列尾部
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
res.add(tmp);
}
return res;
}
}
面试题33. 二叉搜索树的后序遍历序列
class Solution {
public boolean verifyPostorder(int[] postorder) {
Stack<Integer> stack = new Stack<>();
int root = Integer.MAX_VALUE;
for(int i = postorder.length - 1; i >= 0; i--) {
if(postorder[i] > root) return false;
while(!stack.isEmpty() && stack.peek() > postorder[i])
root = stack.pop();
stack.add(postorder[i]);
}
return true;
}
}
面试题34. 二叉树中和为某一值的路径
class Solution {
LinkedList<List<Integer>> res = new LinkedList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> pathSum(TreeNode root, int sum) {
recur(root, sum);
return res;
}
void recur(TreeNode root, int tar) {
if(root == null) return;
path.add(root.val);
tar -= root.val;
if(tar == 0 && root.left == null && root.right == null)
//记录路径时若直接执行 res.append(path) ,则是将 path 列表对象 加入了 res ;后续 path 对象改变时, res 中的 path 对象 也会随之改变(因此肯定是不对的,本来存的是正确的路径 path ,后面又 append 又 pop 的,就破坏了这个正确路径)。list(path) 相当于新建并复制了一个 path 列表,因此不会受到 path 变化的影响。
res.add(new LinkedList(path));
recur(root.left, tar);
recur(root.right, tar);
path.removeLast();
}
}
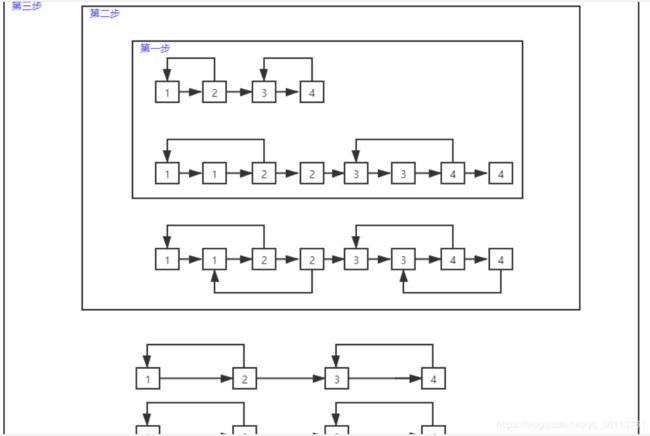
面试题35. 复杂链表的复制
//推荐双百方法二:不需要辅助空间,但是需要额外将两个链表进行拆分,但理解难度较大
public Node copyRandomList2(Node head) {
if(head==null) return null;
copy2(head);
randomAdd2(head);
return build2(head);
}
public void copy2(Node head){
while(head!=null){
Node copy = new Node(head.val);
copy.next = head.next;
head.next =copy;
head = copy.next;
}
}
public void randomAdd2(Node head){
while(head!=null){
if(head.random!=null) head.next.random = head.random.next;
head=head.next.next;
}
}
public Node build2(Node head){
//将链表拆成两个,注意要恢复原有的链表
Node res = head.next;
Node tmp = res;
head.next = head.next.next;//这一步不可缺少,保证第一个复制节点对N N'的分离操作
head = head.next;
while(head!=null){
tmp.next = head.next;
head.next = head.next.next;
tmp=tmp.next;
head = head.next;
}
return res;
}
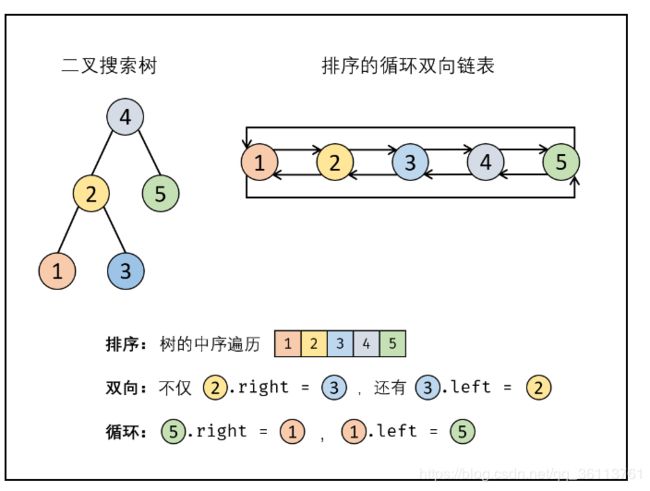
面试题36. 二叉搜索树与双向链表
class Solution {
Node pre, head;
public Node treeToDoublyList(Node root) {
if(root == null) return null;
dfs(root);
head.left = pre;
pre.right = head;
return head;
}
void dfs(Node cur) {
if(cur == null) return;
dfs(cur.left);
if(pre != null) pre.right = cur;
else head = cur;
cur.left = pre;
pre = cur;
dfs(cur.right);
}
}
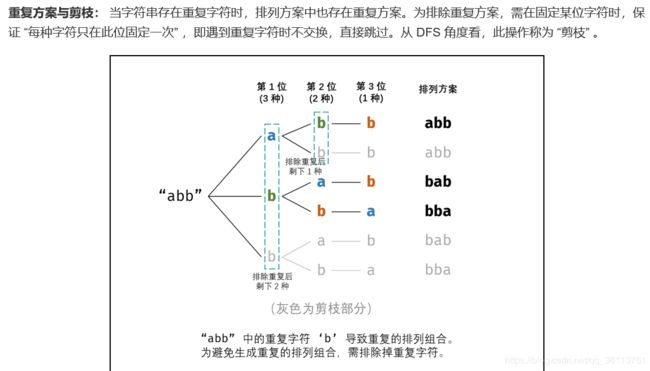
面试题38. 字符串的排列
class Solution {
List<String> res = new LinkedList<>();
char[] c;
public String[] permutation(String s) {
c = s.toCharArray();
dfs(0);
return res.toArray(new String[res.size()]);
}
void dfs(int x) {
if(x == c.length - 1) {
res.add(String.valueOf(c)); // 添加排列方案
return;
}
HashSet<Character> set = new HashSet<>();
for(int i = x; i < c.length; i++) {
if(set.contains(c[i])) continue; // 重复,因此剪枝
set.add(c[i]);
swap(i, x); // 交换,将 c[i] 固定在第 x 位
dfs(x + 1); // 开启固定第 x + 1 位字符
swap(i, x); // 恢复交换
}
}
void swap(int a, int b) {
char tmp = c[a];
c[a] = c[b];
c[b] = tmp;
}
}
面试题43. 1~n整数中1出现的次数
输入一个整数 n ,求1~n这n个整数的十进制表示中1出现的次数。
例如,输入12,1~12这些整数中包含1 的数字有1、10、11和12,1一共出现了5次。



class Solution {
public int countDigitOne(int n) {
int digit = 1, res = 0;
int high = n / 10, cur = n % 10, low = 0;
while(high != 0 || cur != 0) {
if(cur == 0) res += high * digit;
else if(cur == 1) res += high * digit + low + 1;
else res += (high + 1) * digit;
low += cur * digit;
cur = high % 10;
high /= 10;
digit *= 10;
}
return res;
}
}
面试题44. 数字序列中某一位的数字
数字以0123456789101112131415…的格式序列化到一个字符序列中。在这个序列中,第5位(从下标0开始计数)是5,第13位是1,第19位是4,等等。

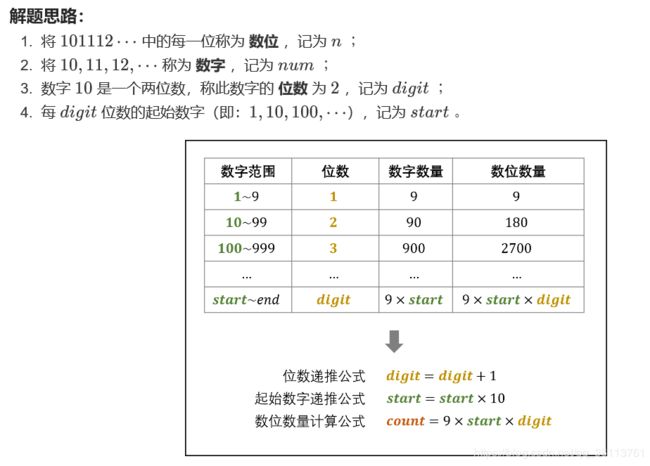
class Solution {
public int findNthDigit(int n) {
int digit = 1;
long start = 1;
long count = 9;
while (n > count) { // 1.
n -= count;
digit += 1;
start *= 10;
count = digit * start * 9;
}
long num = start + (n - 1) / digit; // 2.
return Long.toString(num).charAt((n - 1) % digit) - '0'; // 3.
}
}
面试题45. 把数组排成最小的数
输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。


class Solution {
public String minNumber(int[] nums) {
String[] strs = new String[nums.length];
for(int i = 0; i < nums.length; i++)
strs[i] = String.valueOf(nums[i]);
Arrays.sort(strs, (x, y) -> (x + y).compareTo(y + x));
StringBuilder res = new StringBuilder();
for(String s : strs)
res.append(s);
return res.toString();
}
}
面试题46. 把数字翻译成字符串
给定一个数字,我们按照如下规则把它翻译为字符串:0 翻译成 “a” ,1 翻译成 “b”,……,11 翻译成 “l”,……,25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数,用来计算一个数字有多少种不同的翻译方法。


class Solution {
public int translateNum(int num) {
int a = 1, b = 1, x, y = num % 10;
while(num != 0) {
num /= 10;
x = num % 10;
int tmp = 10 * x + y;
int c = (tmp >= 10 && tmp <= 25) ? a + b : a;
b = a;
a = c;
y = x;
}
return a;
}
}
面试题47. 礼物的最大价值
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?


当 grid矩阵很大时, i=0 或 j=0的情况仅占极少数,相当循环每轮都冗余了一次判断。因此,可先初始化矩阵第一行和第一列,再开始遍历递推。
class Solution {
public int maxValue(int[][] grid) {
int m = grid.length, n = grid[0].length;
for(int j = 1; j < n; j++) // 初始化第一行
grid[0][j] += grid[0][j - 1];
for(int i = 1; i < m; i++) // 初始化第一列
grid[i][0] += grid[i - 1][0];
for(int i = 1; i < m; i++)
for(int j = 1; j < n; j++)
grid[i][j] += Math.max(grid[i][j - 1], grid[i - 1][j]);
return grid[m - 1][n - 1];
}
}
面试题48. 最长不含重复字符的子字符串
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> dic = new HashMap<>();
int res = 0, tmp = 0;
for(int j = 0; j < s.length(); j++) {
int i = dic.containsKey(s.charAt(j)) ? dic.get(s.charAt(j)) : -1; // 获取索引 i
dic.put(s.charAt(j), j); // 更新哈希表
tmp = tmp < j - i ? tmp + 1 : j - i; // dp[j - 1] -> dp[j]
res = Math.max(res, tmp); // max(dp[j - 1], dp[j])
}
return res;
}
}
面试题49. 丑数
我们把只包含因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。

![]()
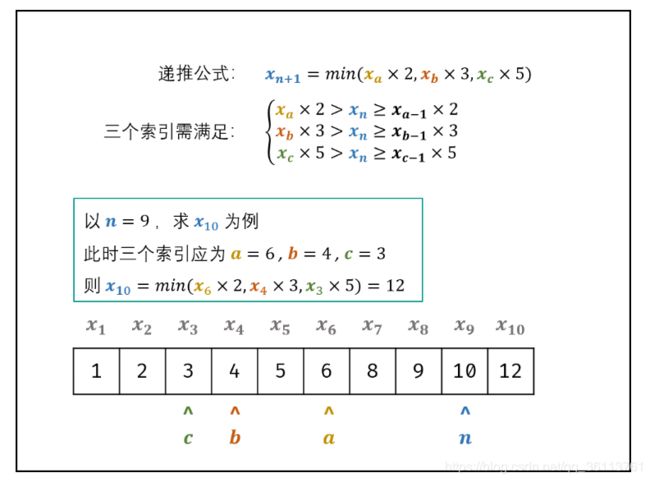
class Solution {
public int nthUglyNumber(int n) {
int a = 0, b = 0, c = 0;
int[] dp = new int[n];
dp[0] = 1;
for(int i = 1; i < n; i++) {
int n2 = dp[a] * 2, n3 = dp[b] * 3, n5 = dp[c] * 5;
dp[i] = Math.min(Math.min(n2, n3), n5);
if(dp[i] == n2) a++;
if(dp[i] == n3) b++;
if(dp[i] == n5) c++;
}
return dp[n - 1];
}
}
面试题56 - I. 数组中数字出现的次数
一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。

class Solution {
public int[] singleNumbers(int[] nums) {
int[] ans = new int[2];
if (nums == null || nums.length < 2 || nums.length % 2 == 1) {
return ans;
}
// 0 和任何数异或都等于该数本身。
int a = 0;
// 用 0 和数组中所有数依次进行异或运算。
for (int num : nums) {
a ^= num;
}
// 得到当前 a 的二进制表达式中最低位的 1 对应的值(负数存储形式为正数取反加一)。
int lowbit = a & (-a);
// 用得到的 lowbit 和数组中所有数依次进行与运算将数组分成两组数。
for (int num : nums) {
// 使得两个只出现一次的数不在同一组,每组分别异或运算得到唯一的数。
if ((num & lowbit) == 0) {
ans[0] ^= num;
} else {
ans[1] ^= num;
}
}
return ans;
}
}
面试题56 - II. 数组中数字出现的次数 II
在一个数组 nums 中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。
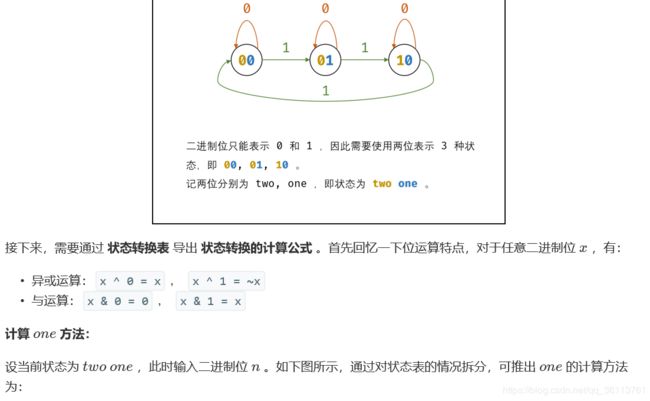
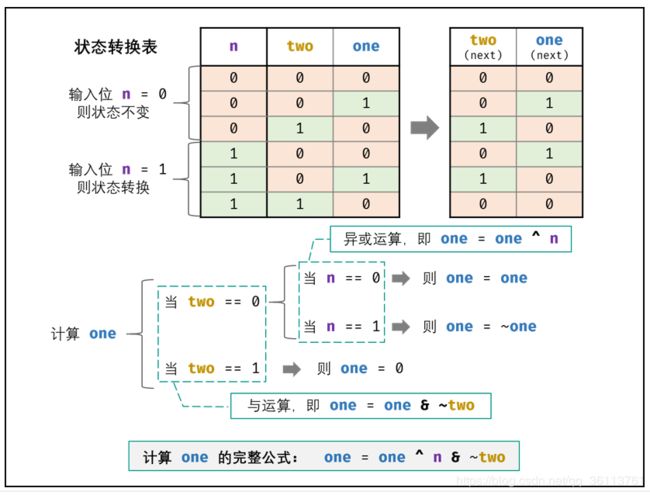
class Solution {
public int singleNumber(int[] nums) {
int ones = 0, twos = 0;
for(int num : nums){
ones = ones ^ num & ~twos;
twos = twos ^ num & ~ones;
}
return ones;
}
}
面试题63. 股票的最大利润
假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次可能获得的最大利润是多少?

class Solution {
public int maxProfit(int[] prices) {
int cost = Integer.MAX_VALUE, profit = 0;
for(int price : prices) {
cost = Math.min(cost, price);
profit = Math.max(profit, price - cost);
}
return profit;
}
}
面试题59 - II. 队列的最大值
请定义一个队列并实现函数 max_value 得到队列里的最大值,要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。
若队列为空,pop_front 和 max_value 需要返回 -1
class MaxQueue {
Queue<Integer> que;
Deque<Integer> deq;
public MaxQueue() {
que = new LinkedList<>(); //队列:插入和删除
deq = new LinkedList<>(); //双端队列:获取最大值
}
public int max_value() {
return deq.size()>0?deq.peek():-1; //双端队列的队首为que的最大值
}
public void push_back(int value) {
que.offer(value); //value入队
while(deq.size()>0 && deq.peekLast()<value){
deq.pollLast(); //将deq队尾小于value的元素删掉
}
deq.offerLast(value); //将value放在deq队尾
}
public int pop_front() {
int tmp = que.size()>0?que.poll():-1; //获得队首元素
//如果是直接peek两个队列的数比较,请注意这样就是在比较两个Integer对象而不是基本类型int,要用equals不要用==,否则对于非缓存数字(-128 - 127)可能会出现明明值一样 == 却返回false的情况!
if(deq.size()>0 && tmp.equals(deq.peek())){
deq.poll(); //如果出队的元素是当前最大值,将deq的队首出队
}
return tmp;
}
}
面试题64. 求1+2+…+n
使用递归解法最重要的是指定返回条件,但是本题无法直接使用 if 语句来指定返回条件。
条件与 && 具有短路原则,即在第一个条件语句为 false 的情况下不会去执行第二个条件语句。利用这一特性,将递归的返回条件取非然后作为 && 的第一个条件语句,递归的主体转换为第二个条件语句,那么当递归的返回条件为 true 的情况下就不会执行递归的主体部分,递归返回。
本题的递归返回条件为 n <= 0,取非后就是 n > 0;递归的主体部分为 sum += Sum_Solution(n - 1),转换为条件语句后就是 (sum += Sum_Solution(n - 1)) > 0。
class Solution {
public int sumNums(int n) {
int sum = n;
boolean b = (n > 0) && ((sum += sumNums(n - 1)) > 0);
return sum;
}
}
面试题67. 把字符串转换成整数
class Solution {
public int strToInt(String str) {
char[] c = str.trim().toCharArray();
if(c.length == 0) return 0;
int res = 0, bndry = Integer.MAX_VALUE / 10;
int i = 1, sign = 1;
if(c[0] == '-') sign = -1;
else if(c[0] != '+') i = 0;
for(int j = i; j < c.length; j++) {
if(c[j] < '0' || c[j] > '9') break;
if(res > bndry || res == bndry && c[j] > '7') return sign == 1 ? Integer.MAX_VALUE : Integer.MIN_VALUE;
res = res * 10 + (c[j] - '0');
}
return sign * (int)res;
}
}
困难
面试题19. 正则表达式匹配
请实现一个函数用来匹配包含’. ‘和’‘的正则表达式。模式中的字符’.‘表示任意一个字符,而’'表示它前面的字符可以出现任意次(含0次)。在本题中,匹配是指字符串的所有字符匹配整个模式。例如,字符串"aaa"与模式"a.a"和"abaca"匹配,但与"aa.a"和"ab*a"均不匹配。
class Solution {
public boolean isMatch(String s, String p) {
char[] str = s.toCharArray();
char[] pstr = p.toCharArray();
int sLen = str.length, pLen = pstr.length;
boolean[][] dp = new boolean[sLen + 1][pLen + 1];
dp[sLen][pLen] = true;
for (int i = sLen; i >= 0; i --) {
// 当 i = sLen 时,即在判断 p[j:] 是否与空串匹配
for (int j = pLen - 1; j >= 0; j --) {
// 判断当前位置的字符是否匹配
boolean isCurMatch = i < sLen && (str[i] == pstr[j] || pstr[j] == '.');
// 如果 p[j + 1] 为 '*',则需要看:
// 1. p[j + 2] 和 s[i:] 是否匹配,若匹配,则 p[j:] 一定匹配
// (因为'*'可以无效化前面的字母)
// 2. 若当前位置的字符匹配,则看 p[j:] 与 s[i + 1] 是否匹配,若匹配,则一定匹配。
// (因为'*'可以重复前面的字母)
if (j + 1 < pLen && pstr[j + 1] == '*') {
dp[i][j] = dp[i][j + 2] || isCurMatch && dp[i + 1][j];
}
// 否则,则看当前是否匹配,以及 p[j + 1] 和 s[i + 1] 是否匹配
else {
dp[i][j] = isCurMatch && dp[i + 1][j + 1];
}
}
}
return dp[0][0];
}
}
面试题37. 序列化二叉树
请实现两个函数,分别用来序列化和反序列化二叉树。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Codec {
//原理:我们可以根据前序遍历的顺序来序列化二叉树,因为前序遍历是从根节点开始的。在遍历二叉树碰到 null时,将其序列化为一个特殊的字符(如'$')
//另外,节点的数值之间要用一个特殊字符(如',')隔开,因为节点的值位数不定且正负不定。
//则下面二叉树 1 可以序列化为:
// / \ [1,2,4,$,$,$,3,5,$,$,6,$,$]
// 2 3
// / / \
// 4 5 6
//我们接着以上述字符串为例分析如何反序列化二叉树。第一个读出的数字是1。由于前序遍历是从根节点开始的,这是根节点的值。
//接下来读出的数字是2,根据前序遍历的规则,这是根节点的左子节点的值。同样,接下来的数字4是值为2的节点的左子节点。
//接着从字符串里读出两个字符'$',这表明值为4的节点的左、右子节点均不存在,因此它是一个叶节点。接下来回到值为2的节点,重建它的右子节点。
//由于下一个字符是'$',这表明值为2的节点的右子节点不存在, 2这个节点的左、右子树都己经构建完毕,接下来回到根节点,反序列化根节点的右子树
//下一个序列化字符串中的数字是3,因此右子树的根节点的值为3。它的左子节点是一个值为5的叶节点,因为接下来的三个字符是"5,$,$"。
//同样,它的右子节点是值为6的叶节点,因为最后3个字符是"6,$,$"。
int start=0;//注意这里必须是全局变量,否则后面的迭代过程中start无法正确变化
public String serialize(TreeNode root) {
if(root==null) return "$";
StringBuilder res = new StringBuilder();
recur(root,res);
return res.toString();
}
public void recur(TreeNode root,StringBuilder res){//前序遍历
if(root==null){
res.append("$,");//可以append string
return;}
res.append(root.val);//append int 由于int位数不定,且可正可负,因此各元素间必须用,分割
res.append(',');//append char
recur(root.left,res);
recur(root.right,res);
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
if(data.equals("$")) return null;//Sting值相等的判别不能用==
String inputs[] = data.split(",");
//虽然data中以,结尾,但是上述分割后会默认最后一个,不存在 不会使最后一个分割元素为空
return build(inputs);
}
public TreeNode build(String[] inputs){
TreeNode res;
if(inputs[start].equals("$")){
start++;
return null;//这里说明当前节点为null,自然不存在左右节点了,直接返回
}
res = new TreeNode(Integer.parseInt(inputs[start]));
start++;
//注意:start不能以形参的形式引入build方法中,build(inputs,start);如果是这样
//下面res.left = build(inputs,start); res.right = build(inputs,start+1);由于处于同一级迭代中start值连续
//但实际上res.right中应该是上面res.left迭代完成后才会执行的,start不连续,因此把start作为全局变量较为合适
res.left = build(inputs);
res.right = build(inputs);
return res;
}
}
// Your Codec object will be instantiated and called as such:
// Codec codec = new Codec();
// codec.deserialize(codec.serialize(root));
面试题51. 数组中的逆序对
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。 归并排序
为什么当左边的数比右边的数小时统计逆序对?
左边一直比右边大 那左边的数和当前右边的数都可以组成一个逆序对 那怎么统计一共有多少个或是说直到什么时候为止呢 直到左边比右边小时 ,那左边的数和右边当前角标之前的数 都是逆序的。
/**
*归并排序稍作修改
*O(N*logN)
*O(N)
*/
class Solution {
//记录答案
private int res = 0;
public int reversePairs(int[] nums) {
int len = nums.length;
//为了不改变原数组 新copy个数组进行计算
int[] copy = new int[len];
for(int i=0;i<len;i++){
copy[i]=nums[i];
}
//归并排序
mergeSort(copy,0,len-1);
return res;
}
/**
*nums 待排序数组
*left 当前待排序区间的左下标
*right 当前待排序区间的右下标
*/
private void mergeSort(int[] nums,int left,int right){
if(left>=right)return;
//求中点 划分左右两个区间 递归排序
int mid = (left+right)/2;
mergeSort(nums,left,mid);
mergeSort(nums,mid+1,right);
//利用一个tmp辅助数组 开始对左右两个排序后的区间合并
int l = left,r=mid+1,cur=0;
int[] tmp = new int[right-left+1];
while(l<=mid&&r<=right){
//左边区间数小于等于右边 左边先放入tmp 并更新左边指针
if(nums[l]<=nums[r]){
tmp[cur]=nums[l++];
//相对于正常归并排序多出的一个步骤 计算有多少个逆序对
res+=r-(mid+1);
}else{
tmp[cur]=nums[r++];
}
cur++;
}
//如果右边节点先到右区间边界导致上边while退出
while(l<=mid){
tmp[cur++]=nums[l++];
//相对于正常归并排序多出的一个步骤 计算有多少个逆序对
res+=r-(mid+1);
}
while(r<=right){
tmp[cur++]=nums[r++];
}
//将待排序数组 当前排好序的left~right区间重新赋值
for(int i=0;i<tmp.length;i++){
nums[left+i]=tmp[i];
}
}
}
面试题41. 数据流中的中位数
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值

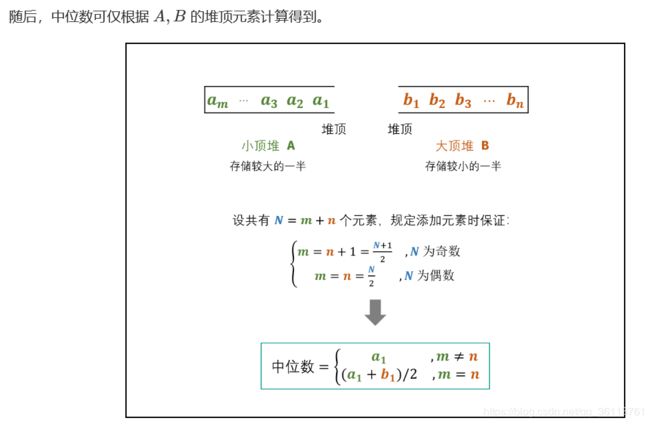

class MedianFinder {
Queue<Integer> A, B;
public MedianFinder() {
A = new PriorityQueue<>(); // 小顶堆,保存较大的一半
B = new PriorityQueue<>((x, y) -> (y - x)); // 大顶堆,保存较小的一半
}
public void addNum(int num) {
if(A.size() != B.size()) {
A.add(num);
B.add(A.poll());
} else {
B.add(num);
A.add(B.poll());
}
}
public double findMedian() {
return A.size() != B.size() ? A.peek() : (A.peek() + B.peek()) / 2.0;
}
}