机器学习中的分类器：感知机、逻辑回归、支持向量机

  深度神经网络(Deep Neural Networks，DNN)是深度学习的基础，由于神经网路是基于感知机模型的扩展，因此多层感知机(Multi-Layer perceptron，MLP)就可以看作是深度神经网络。在深度学习中，用于分类的卷积神经网络(Convolutional Neural Networks, CNN)，一般都会在全连接层(FC)之后使用softmax分类器，softmax函数可以看作是logistic函数（Sigmoid）的一般形式。当然，也有例如目标检测的经典网络RCNN，是将感兴趣区域提取的CNN特征输入到支持向量机(SVM)进行分类。为了更好地理解深度学习中的内容，以及发现深度学习对机器学习的继承性，我将上面描述的感知机(Perceptron)、逻辑回归(Logistic Regression，LR)、支持向量机(Support Vector Machine, SVM)这三种基础的分类器进行了整理。这是一篇需要数学基础的总结，做好迎接大量公式的准备吧。

感知机

  1957年，美国神经学家Frank Rosenblatt提出了可以模拟人类感知能力的机器，并称之为“感知机”，研究成果于1958年发表在《The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain》。感知机是人工神经网络的进一步发展，人工神经网络的概念及人工神经元的数学模型是1943年在《A logical calculus of the ideas immanent in nervous activity》论文中提出。感知机可以被视为一种最简单形式的前馈神经网络（即每个神经元只与前一层的神经元相连，各层间没有反馈），是一种二元线性分类器。二元线性分类器意味着，分类器尝试对于输入的多维数据找到一个超平面（二维数据是找到一条直线），能够把所有的二元类别分隔开。当然，如果数据不是线性可分的时候，感知机的局限性就显现出来了。

感知机模型

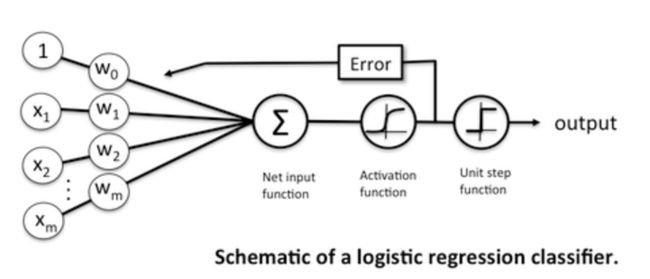
  为了模拟神经细胞的行为，神经元模型提出了与之对应的基础概念，如权重（突触）、偏置（阈值）及激活函数（细胞体）。感知机由两层神经元组成，输入层接收外界输入信号后传递给输出层。假设输入的m个样本数据可以表示为:$(x_1^{(1)},x_2^{(1)},...x_n^{(1)},y_1)$，$(x_1^{(2)},x_2^{(2)},...x_n^{(2)},y_2)$，… $(x_1^{(m)},x_2^{(m)},...x_n^{(m)},y_m)$，其中向量$x\text{x}x$有n维特征，$y\text{y}y$每一维限制在两个取值中，代表着样本的类别。那么感知机需要预测的输出为：一类样本 $w_1{x}_1+...+w_n{x}_n+\theta >0$，另一类样本 $w_1{x}_1+...+w_n{x}_n+\theta <0$。再经过一个神经元激活函数，$sign(x)=\{\begin{array}{ll}-1& x<0\\ 1& x\ge 0\end{array}$。在 $\theta$ 处增加一个特征 $x_0=1$，这样权重和阈值的学习统一为权重的学习，得到分类结果 $y_{pred}=sign(w\text{w}w\bullet x\text{x}x)$。上述激活函数可以保证，在预测正确的时候 $y_{pred}\times y\ge 0$。感知机结构如下图所示：

感知机的训练过程

  感知机的训练过程较为简单，基本思想是：若感知机对训练样本 $({x\text{x}x}^{(i)},y_i)$ 预测正确，则感知机不发生变化，否则将根据错误的程度进行权重调整。感知机的损失函数是 $J(w)=-\sum _{x^{(i)}\in M}{y}_i{w\text{w}w}^{(i)}\bullet {x\text{x}x}^{(i)}$，其中M是所有误分类的数据的集合，即当预测正确的时候损失函数为0，只有当预测错误的时候损失函数是一组正数的和。由于符号函数的不连续性，这里没有使用标准的均方误差。误差函数的优化问题可以由梯度下降法或者牛顿法来解决，随机梯度下降每次仅仅需要使用一个误分类的数据来更新梯度，用损失函数对样本 $i$ 的权重向量求偏导$\frac{\partial }{\partial w}J(w)=-y_i{x}^{(i)}$，用该梯度对权重进行更新 $w=w+\alpha y_i{x}^{(i)}$，其中 $\alpha$ 为学习率。

感知机的局限性和发展

  从上图可以看出，感知机只有输出层神经元进行激活函数处理，即只拥有一层功能神经元，其学习能力非常有限。如果是线性可分的模型，感知机的学习过程一定会收敛，最后求得适当的权向量；否则感知机的学习过程将会发生震荡，权值难以稳定。“与”、“或”、“非”问题感知机都可以解决，但是无法学习比较复杂的非线性模型，像“异或”问题。因此DNN在感知机的基础上做了扩展，主要有以下三点：

• 增加了隐藏层，增强了模型的表达能力和非线性；
• 输出层的神经元数量增多，可以更灵活地处理分类问题；
• 对激活函数做了修改，处理能力有限的符号函数用sigmoid函数进行替换。

参考链接：https://www.cnblogs.com/pinard/p/6418668.html

神经网络的反向传播算法

  尽管DNN的学习能力比单层感知机强得多，但是训练多层网络比单层网络也变得困难。反向传播(Backpropagation，BP)算法是一种与最优化方法（如梯度下降法）结合使用的，训练神经网络最有效的算法。1974年哈佛大学的Paul Werbos在论文《Beyond regression: new fools for prediction and analysis in the behavioral sciences》中发明了BP算法，但是由于当时正值神经外网络低潮期，并未受到应有的重视。反向传播算法的几个特点：

• 通常被认为是一种监督学习方法：要求有对每个输入值期望得到的已知输出，来计算损失函数的梯度。然而，它也用在一些无监督网络（如自动编码器）中。
• 用链式法则对每层迭代计算梯度，是多层前馈网络的Delta规则（权值的修正量等于误差乘以输入）的推广。
• 要求人工神经元的激活函数可微。

算法流程：
输入：神经网络结构（各层神经元数量及网络层数L），批量m个样本，损失函数，sigmoid激活函数用$\sigma$表示，迭代步长（学习率）$\alpha$，最大迭代次数MAX，停止迭代阈值为ϵ。
输出：权重矩阵$w\text{w}w$和偏置向量$b\text{b}b$。
（1）初始化网络权值（通常是小的随机值）。
（2）for iter in 1 to Max:
（2-1）for i in 1 to m:

• 输入样本$x^{(i)}$;
• for $l$ = 2 to L：进行前向传播算法计算隐藏层的输出;
• 通过损失函数计算输出层的误差；
• for $l$ = L-1 to 2：进行反向传播算法计算隐藏层的误差；

（2-2）for $l$ = 2 to L，更新第$l$层的权重和偏置。
（2-3）如果所有的 $w\text{w}w$ 和 $b\text{b}b$ 的变化值都小于停止迭代阈值ϵ，则跳出迭代循环到步骤（3）。
（3）输出更新后的权重矩阵$w\text{w}w$和偏置向量$b\text{b}b$。

由于网络隐藏层输出的真实值无法求得，所以反向传播算法主要是解决了隐藏层的误差计算，只要根据误差每一层的权重更新便很容易通过求梯度获得，推导过程如下：

1. 前向传播计算 $l$ 层输出：$ou{t}^l=\sigma (ne{t}^l)=\sigma (W^{l}ou{t}^{l-1}+b^l)$
2. 误差函数使用最常见的均方差来度量损失：$J(W,b,x,y)=\frac{1}{2}||ou{t}^L-y|{|}_2^2$
   由于输出层可能有多个神经元，如上图所示，则最后一层的损失是多个神经元损失的和：$E_{total}=\sum \frac{1}{2}(ou{t}^L-y{)}^2=E_{o1}+E_{o2}$
3. 计算输出层的权值更新，以 $w_5$ 为例（链式法则）：
   $$\frac{\partial E_{total}}{\partial w_5}=\frac{\partial E_{total}}{\partial ou{t}_{o1}}\ast \frac{\partial ou{t}_{o1}}{\partial ne{t}_{o1}}\ast \frac{\partial ne{t}_{o1}}{\partial w_5}$$
   其中，
   $$由于ne{t}_{o1}=ou{t}_{h_1}\ast w_5+ou{t}_{h_2}\ast w_6+b_2，可得\frac{\partial ne{t}_{o1}}{\partial w_5}=ou{t}_{h_1}（前向传播已经求得）。$$
   $$由于ou{t}_{o1}=\sigma (ne{t}_{o1})=\frac{1}{1+e^{-ne{t}_{o1}}}，可得\frac{\partial ou{t}_{o1}}{\partial ne{t}_{o1}}=ou{t}_{o1}\ast (1-ou{t}_{o1})。(利用sigmoid函数导数f^{{}^{\prime }}(x)=f(x)(1-f(x)))$$
   $$由于E_{total}=\frac{1}{2}(ou{t}_{o1}-targe{t}_{o1}{)}^2+\frac{1}{2}(ou{t}_{o2}-targe{t}_{o2}{)}^2，可得\frac{\partial E_{total}}{\partial ou{t}_{o1}}=ou{t}_{o1}-targe{t}_{o1}。$$
   可以将输出层的误差表示为：$${\delta }_{o1}=\frac{\partial E_{total}}{\partial ou{t}_{o1}}\ast \frac{\partial ou{t}_{o1}}{\partial ne{t}_{o1}}，则\frac{\partial E_{total}}{\partial w_5}={\delta }_{o1}\ast ou{t}_{h_1}$$
   同理对于 $w_6$ 有 $\frac{\partial E_{total}}{\partial w_6}={\delta }_{o1}\ast ou{t}_{h_2}$，对 $w_7$ 有 $\frac{\partial E_{total}}{\partial w_7}={\delta }_{o2}\ast ou{t}_{h_1}$，对 $w_8$ 有 $\frac{\partial E_{total}}{\partial w_8}={\delta }_{o2}\ast ou{t}_{h_2}$。
   那么更新 $w_5$ 的值：$$w_5^{+}=w_5-\alpha \ast \frac{\partial E_{total}}{\partial w_5}$$
4. 计算隐藏层的权值更新，以 $w_1$ 为例（链式法则）：
   $$\frac{\partial E_{total}}{\partial w_1}=\frac{\partial E_{total}}{\partial ou{t}_{h_1}}\ast \frac{\partial ou{t}_{h_1}}{\partial ne{t}_{h_1}}\ast \frac{\partial ne{t}_{h_1}}{\partial w_1}$$
   类似上面的推导，可以直接得到$\frac{\partial ne{t}_{h_1}}{\partial w_1}=i_1$，$\frac{\partial ou{t}_{h_1}}{\partial ne{t}_{h_1}}=ou{t}_{h_1}\ast (1-ou{t}_{h_1})$。
   但是损失函数是由不同的支路求得的，所以$$\frac{\partial E_{total}}{\partial ou{t}_{h_1}}=\frac{\partial E_{o1}}{\partial ou{t}_{h_1}}+\frac{\partial E_{o2}}{\partial ou{t}_{h_1}}$$
   其中，$$\frac{\partial E_{o1}}{\partial ou{t}_{h_1}}=\frac{\partial E_{o1}}{\partial ou{t}_{o1}}\ast \frac{\partial ou{t}_{o1}}{\partial ne{t}_{o1}}\ast \frac{\partial ne{t}_{o1}}{\partial ou{t}_{h_1}}={\delta }_{o1}\ast w_5$$
   同理，$$\frac{\partial E_{o2}}{\partial ou{t}_{h_1}}={\delta }_{o2}\ast w_6$$
   $$\frac{\partial E_{total}}{\partial w_1}=({\delta }_{o1}\ast w_5+{\delta }_{o2}\ast w_6)\ast ou{t}_{h_1}\ast (1-ou{t}_{h_1})\ast i_1={\delta }_{h1}\ast i_1$$
   接下来的更新方法相同。

参考链接：https://www.cnblogs.com/charlotte77/p/5629865.html

总结

  可以看出，如果网络有多个隐藏层的话，隐藏层的误差有一种递归计算的形式，前一层的误差依赖于后一层的误差，再结合本层的输出和输入最后得到梯度值。根据这种规律计算出误差之后，参数的更新就变得简单起来。尽管从感知机到神经网络，增加网络层数使得表达能力更强，但是这样的网络训练仍然会带来梯度消失和梯度爆炸等问题（现在就可以从反向传播的公式清晰地看出来啦），优化过程容易陷入局部极小值，出现过拟合或者欠拟合问题。因此，神经网络逐渐发展了针对此类问题的解决方法。

逻辑回归

  逻辑回归(logistic函数)的分类 vs 神经网络的sigmoid激活函数与softmax分类器的分类，这两者在刚接触的时候就一直觉得知识点联系很大，数学原理相似但又是两个不同的分类模型。所以，为了弄清楚这两者之间的联系，再回顾一下机器学习中的逻辑回归。逻辑回归最早由统计学家David Cox在他1958年的论文《The regression analysis of binary sequences》中提出来的。虽然逻辑回归用来处理分类任务，但其实是在回归任务上发展的分类任务，通过回归拟合样本属于某一类别的概率，然后通过限定阈值或其他方式将其贴上标签。

  逻辑回归是当前业界比较常用的机器学习方法，它与多元线性回归同属一个家族，即广义线性模型。由于模型的学习方式，Logistic 回归的预测结果也可以用作给定数据实例属于类 0 或类 1 的概率，这对于需要为预测结果提供更多理论依据的问题非常有用。与线性回归类似，当删除与输出变量无关以及彼此之间非常相似或相关的属性后，Logistic 回归的效果更好。该模型学习速度快，对二分类问题十分有效。

  像线性回归一样，Logistic回归的目的也是找到每个输入变量的权重系数值。但不同的是，还需找一个单调可微函数将分类任务的真实标记 y 与线性回归模型的预测值联系起来。Logistic回归舍弃了用单位阶跃函数进行二分类标签的映射，而是利用了能在一定程度上近似它的替代函数，所以输出的预测结果是通过logistic非线性函数变换而来的。假设数据服从伯努利分布（0-1分布），通过极大化似然函数的方法，运用梯度下降来求解参数，达到将数据二分类的目的。

模型分析

线性回归：$y={w\text{w}w}^{T}x\text{x}x+b$
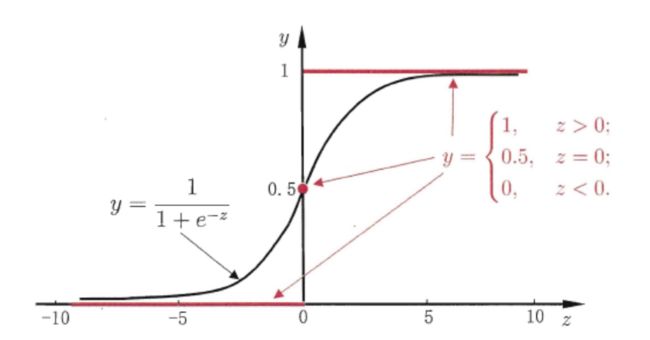
经过对数几率函数变换：$y=\frac{1}{1+e^{-(w^{T}x+b)}}$，对数几率函数是任意阶可导的凸函数，许多数值优化算法都可以求出其最优解。
对数几率：$ln\frac{y}{1-y}={w\text{w}w}^{T}x\text{x}x+b$，y 代表正样本的可能性，1-y 代表负样本的可能性。
如果 $\frac{y}{1-y}\ge 1$，即 $y\ge 0.5$，则认为输出的为类 1；否则 $\frac{y}{1-y}<1$，则认为输出的为类 0。
决策边界：${w\text{w}w}^{T}x\text{x}x+b=0$
将 y 视为类后验概率估计 $p(y=1|x\text{x}x)$，则 1-y 可以视为 $p(y=0|x\text{x}x)$，对数几率可写为：$$ln\frac{p(y=1|x\text{x}x)}{p(y=0|x\text{x}x)}={w\text{w}w}^{T}x\text{x}x+b$$
显然有： $p(y=1|x\text{x}x)=\frac{e^{w^{T}x+b}}{1+e^{w^{T}x+b}}=\pi (x)$， $p(y=0|x\text{x}x)=\frac{1}{1+e^{w^{T}x+b}}=1-\pi (x)$
为了使每个样本属于其真实标记的概率越大越好，使用极大似然法来估计$w\text{w}w$ 和 $b$。
似然函数：${\Pi }_{i=1}^m[\pi (x^{(i)}){]}^{y^{(i)}}[1-\pi (x^{(i)}){]}^{1-y^{(i)}}$
对数似然函数：
$$L(w)=\log {\Pi }_{i=1}^m[\pi (x^{(i)}){]}^{y^{(i)}}[1-\pi (x^{(i)}){]}^{1-y^{(i)}}=\sum _{i=1}^m[y^{(i)}\log \pi (x^{(i)})+(1-y^{(i)})\log (1-\pi (x^{(i)}))]$$

损失函数

最大化似然函数等价于求$-L(w)$的极小值，即二值交叉熵损失(binary cross entropy)：
$$J(w)=-\frac{1}{m}\sum _{i=1}^m(y^{(i)}\log \pi (x^{(i)})+(1-y^{(i)})\log (1-\pi (x^{(i)})))$$
将上述公式对权重求偏导：
$$\frac{\partial }{\partial w_j}J(w)=\frac{1}{m}\sum _{i=1}^m(\pi (x^{(i)})-y^{(i)})x_j^{(i)}$$
梯度下降公式为：
$$w_j^{+}=w_j-\alpha \frac{1}{m}\sum _{i=1}^m(\pi (x^{(i)})-y^{(i)})x_j^{(i)}$$

softmax多分类

二项逻辑回归的参数估计法可以推广到多项逻辑回归，即softmax（或称归一化指数函数，是逻辑函数的一种推广），此时有：
$$\pi (x{)}_c=\frac{e^{w_c^T\cdot x}}{{\sum }_{k=1}^C{e}^{w_k^T\cdot x}}$$
极大似然估计：$L(w)={\prod }_{i=1}^n\pi (x^{(i)}{)}^{y^{(i)}}$
第 i 个样本的多类交叉熵损失：
$$J(w)=-\sum _{k=1}^C(y_k^{(i)}\log \pi (x^{(i)}{)}_k)$$

逻辑回归与神经网络的关系

• 逻辑回归与感知机都为二元线性分类器，训练方法都是使用梯度下降，但是二者的激活函数分别为sigmoid函数和sign函数，输出类别分别为0/1和-1/1。
• 上述DNN中使用了sigmoid函数，但是损失函数用的是均值平方差损失(Mean Square Error，MSE)；而逻辑回归使用的是交叉熵损失(Cross Entropy，CE)。在使用sigmoid激活函数时，MSE Loss求得的梯度包含σ′(x)，因此存在反向传播收敛速度慢的问题；而CE Loss的梯度不包含σ′(z)。通常情况下，在使用sigmoid激活函数时，利用CE Loss肯定比MSE Loss效果更好。
• 实际上，可以将Logistic Regression看做是仅含有一个神经元的单层的神经网络。

总结

  LR不仅预测出类别，还可得到近似概率预测，可以做排序模型。训练快，在使用特征工程后效果更好，并且添加特征简单。容易使用和解释，计算代价低，对时间和内存需求较为高效。但是容易欠拟合（增加特征维度来解决），分类精度不高，而且只能处理两分类问题。过拟合时加入正则化（L1和L2惩罚）。

参考链接：
[1] https://www.cnblogs.com/makefile/p/logistic-regression.html
[2] https://zhuanlan.zhihu.com/p/56900935

支持向量机

  支持向量的概念早在二十世纪六十年代就已经出现，而支持向量机是Cortes和Vapnik在1995年的论文《Support vector networks》中正式发表。SVM是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。随着训练数据的复杂，支持向量机学习方法也由简至繁的发展，简单模型是复杂模型的基础，也是复杂模型的特殊情况。当训练数据线性可分时，通过硬间隔最大化，学习一个线性的分类器；当训练数据近似线性可分时，通过软间隔最大化，也学习一个线性的分类器；当训练数据线性不可分时，通过使用核技巧和软间隔最大化，学习非线性支持向量机。

线性可分支持向量机

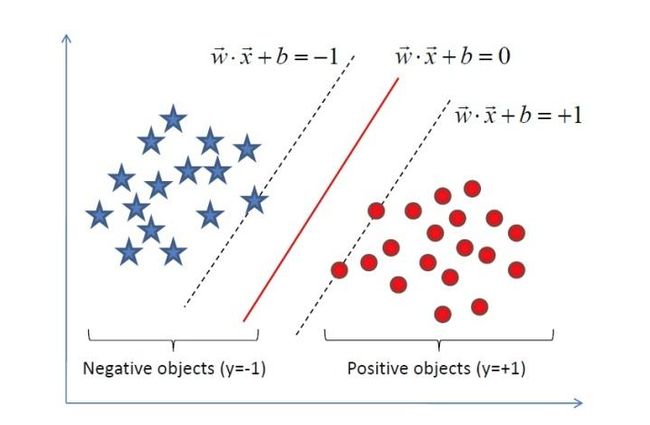
  前面提到过，二元线性分类器尝试对于输入的多维数据划分一个超平面，将所有不同类别的样本分隔开。但是，这样的超平面可能有很多个，感知机利用误分类最小的策略，求得分类超平面；而支持向量机利用最大间隔求最优的决策面。显然，这是一个最优化问题，因此我们需要构造目标函数和优化对象。在线性SVM算法中，目标函数是"分类间隔"，优化对象是决策面。

• 决策面：${w\text{w}w}^{T}x\text{x}x+b=0$，其中$w\text{w}w=(w_1,w_2,...,w_n)$为超平面的法向量，$b$为截距。
• 几何间隔：给定直线 $Ax+By+C=0$，由点到直线的距离公式 $d=|\frac{Ax+By+C}{\sqrt{A^2+B^2}}|$，可以得到多维空间中点到决策面的距离为$\frac{|w^{T}x+b|}{||w||}$。假设正样本标记为1，负样本标记为-1，那么样本的几何间隔 ${\gamma }_i=y_i((\frac{w}{||w||}{)}^T{x}_i+\frac{b}{||w||})$。训练集对于超平面的几何间隔为所有样本几何间隔的最小值，$\gamma =\underset{i=1,2,...,m}{\min }{\gamma }_i$
• 硬间隔最大化：可以表示为下面的约束最优化问题
  $$\underset{w,b}{\max }\gamma ，s.t.y_i((\frac{w}{||w||}{)}^T{x}_i+\frac{b}{||w||})\ge \gamma ，i=1,2,...,m$$
  由于函数间隔$\gamma$并不影响最优化问题的解，因此等价于：
  $$\underset{w,b}{\max }\frac{1}{||w||}，s.t.y_i(w^T{x}_i+b)-1\ge 0，i=1,2,...,m$$
  最大化$\frac{1}{||w||}$和最小化$\frac{1}{2}||w|{|}^2$是等价的，最终得到：
  $$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2，s.t.y_i(w^T{x}_i+b)-1\ge 0，i=1,2,...,m$$
  这是一个含有不等式约束的凸二次规划问题，维度较多时，可以对其使用拉格朗日乘子法得到其对偶问题，通过求解对偶问题得到原始问题的最优解，由于上述约束条件是不等式约束，从而还需要用到KKT条件。对比之前无约束的优化问题，是通过求函数对于变量的导数，令其为0，就找到了函数的候选极值点。

• 拉格朗日函数：拉格朗日方程将约束条件放到目标函数中，从而将有约束优化问题转换为无约束优化问题。该函数在可行解区域内与原目标函数完全一致，而在可行解区域外的数值非常大。
  $$L(w\text{w}w,b,\alpha \text{α}\alpha )=\frac{1}{2}||w|{|}^2-\sum _{i=1}^m{\alpha }_i(y_i(w^T{x}_i+b)-1)$$
  其中，${\alpha }_i$是拉格朗日乘子，${\alpha }_i\ge 0$，$\alpha \text{α}\alpha =({\alpha }_1,{\alpha }_2,...,{\alpha }_m)$。
  由于$\underset{{\alpha }_i\ge 0}{\max }L(w\text{w}w,b,\alpha \text{α}\alpha )$在可行域内为$\frac{1}{2}||w|{|}^2$，在非可行域内为正无穷。所以上述的优化问题可以变为：
  $$\underset{w,b}{\min }\underset{{\alpha }_i\ge 0}{\max }L(w\text{w}w,b,\alpha \text{α}\alpha )$$
• 对偶算法：上述拉格朗日函数，使用求导的方法求解依然困难。因此使用拉格朗日对偶性，将不易求解的优化问题转化为易求解的优化。
  $$\underset{{\alpha }_i\ge 0}{\max }\underset{w,b}{\min }L(w\text{w}w,b,\alpha \text{α}\alpha )$$
  该对偶问题的具体形式可以通过以下求解完成：
  （1）先求解内侧的最小化：固定${\alpha }_i$，对$w\text{w}w,b$分别求偏导数，令偏导数为0
  $$w\text{w}w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i,0=\sum _{i=1}^m{\alpha }_i{y}_i$$
  将$L(w\text{w}w,b,\alpha \text{α}\alpha )$中的$w\text{w}w,b$消去，可得：
  $$L(w\text{w}w,b,\alpha \text{α}\alpha )=\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$$
  （2）求外侧的最大值：
  $$\underset{\alpha }{\max }(\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j),s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i\ge 0,i=1,2,...,m$$

对偶问题和原始问题等价必须要满足（1）求取最小值的目标函数为凸函数的一类优化问题；（2）需要满足KKT条件。

• KKT(Karush-Kuhn-Tucker)条件：
  $$\{\begin{array}{r}{\alpha }_i\ge 0\\ y_i(w^T{x}_i+b)-1\ge 0\\ {\alpha }_i(y_i(w^T{x}_i+b)-1)=0\end{array}$$
  于是，对于任意样本总有 ${\alpha }_i=0$ 或者 $y_i(w^T{x}_i+b)-1=0$。若 ${\alpha }_i>0$，则必有 $y_i(w^T{x}_i+b)-1=0$，此时对应的样本 $i$ 位于最大间隔边界上，是一个支持向量。
  所以原始最优化问题的解通过求得对偶问题中的最优化解 ${\alpha }_i^{\ast }$ ，其中至少有一个 ${\alpha }_i^{\ast }>0$。然后可按下式求得 ${w\text{w}w}^{\ast },b^{\ast }$，并且${w\text{w}w}^{\ast },b^{\ast }$ 只依赖于支持向量:
  $$\begin{gathered} {w\text{w}w}^{\ast }=\sum _{i=1}^m{\alpha }_i^{\ast }{y}_i{x}_i \\ {b}^{\ast }=y_j-\sum _{i=1}^m{\alpha }_i^{\ast }{y}_i(x_i^T{x}_j)，存在j使得{\alpha }_j^{\ast }>0 \end{gathered}$$

算法流程：
输入：线性可分训练集m个样本。
输出：分隔超平面和分类决策函数。
（1）构造并求解约束最优化问题
$$\begin{gathered} \underset{\alpha }{\max }(\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j) \\ s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0,{\alpha }_i\ge 0,i=1,2,...,m \end{gathered}$$
求得最优解${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },...,{\alpha }_m^{\ast })$。
（2）计算 ${w\text{w}w}^{\ast }=\sum _{i=1}^m{\alpha }_i^{\ast }{y}_i{x}_i$，并选择${\alpha }^{\ast }$的一个正分量 ${\alpha }_j^{\ast }>0$，计算 $b^{\ast }=y_j-\sum _{i=1}^m{\alpha }_i^{\ast }{y}_i(x_i{x}_j)$。
（3）求得分隔超平面 $(w^{\ast }{)}^{T}x+b^{\ast }=0$ 和分类决策函数 $f(x)=sign((w^{\ast }{)}^{T}x+b^{\ast })$
那么如何求得${\alpha }^{\ast }$，1996年Platt提出了SMO(Sequential Minimal Optimizaion)算法用于训练SVM。一旦求出了${\alpha }^{\ast }$，就很容易计算出权重向量并得到分隔超平面。

软间隔支持向量机

  实际任务中，很难确定训练样本在特征空间中线性可分，也很难断定特征空间线性可分的结果可能是由于过拟合造成的。所以引入了“软间隔”的概念，允许向量机在一些样本上出错，而其余绝大部分样本都是线性可分的。

• 松弛变量 ${\xi }_i\ge 0$：约束条件变为 $y_i(w^T{x}_i+b)\ge 1-{\xi }_i$
• 损失函数：对每一个松弛变量添加代价C，C决定了误分类的程度。$\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\xi }_i$，即
  $$\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m\max (0,1-y_i(w^T{x}_i+b))$$
  $max(0,1-z)$ 是hinge loss，因此该损失函数可以看做是加了正则化的hinge loss。
• 原始优化问题：
  $$\begin{gathered} \underset{w,b,\xi }{\min }\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\xi }_i \\ s.t.y_i(w^T{x}_i+b)\ge 1-{\xi }_i，i=1,2,...,m \\ {\xi }_i\ge 0，i=1,2,...,m \end{gathered}$$

后面与线性可分支持向量机的优化方式相同。

• 拉格朗日函数：
  $$L(w\text{w}w,b,\alpha \text{α}\alpha )=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\xi }_i-\sum _{i=1}^m{\alpha }_i(y_i(w^T{x}_i+b)-1+{\xi }_i)-\sum _{i=1}^m{\mu }_i{\xi }_i$$
• 对偶问题：
  $$\begin{gathered} \underset{\alpha }{\max }(\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j) \\ s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0,C-{\alpha }_i-{\mu }_i=0,{\alpha }_i\ge 0,,{\mu }_i\ge 0,i=1,2,...,m \end{gathered}$$
• KKT条件：
  $$\{\begin{array}{r}{\alpha }_i\ge 0,{\mu }_i\ge 0\\ y_i(w^T{x}_i+b)-1+{\xi }_i\ge 0\\ {\alpha }_i(y_i(w^T{x}_i+b)-1+{\xi }_i)=0\\ {\xi }_i\ge 0,{\mu }_i{\xi }_i=0\end{array}$$
• 最优解：
  $$\begin{gathered} {w\text{w}w}^{\ast }=\sum _{i=1}^m{\alpha }_i^{\ast }{y}_i{x}_i \\ {b}^{\ast }=y_j-\sum _{i=1}^m{\alpha }_i^{\ast }{y}_i(x_i^T{x}_j) \end{gathered}$$
  可以看出，软间隔支持向量的最终模型也只与支持向量有关。

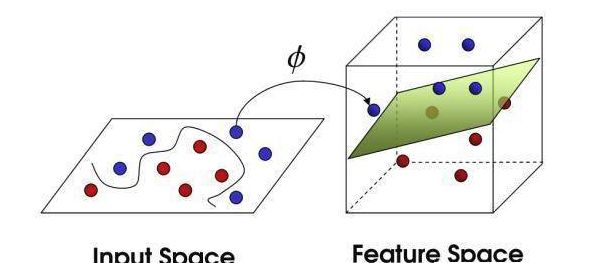
  对于非线性分类问题，可以通过非线性变换，将它从原始空间映射到更高维的特征空间中，使得样本在这个特征空间线性可分，因此可以在高维特征空间中学习线性支持向量机。由于在线性支持向量机学习的对偶问题里，目标函数和分类决策函数都只涉及样例之间的内积，所以利用核技巧，用核函数替换其中的内积达到非线性变换。核技巧同样可以用于逻辑回归。

更多关于SMO算法和核函数的内容可以参考下面的文献：
[1]《统计学习方法》 李航著
[2]《机器学习》周志华著

SVM vs 感知机和逻辑回归

这三者都是属于监督学习的一种分类器（决策函数），分类决策面都是线性的（不考虑核函数）。中心思想都是，增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。

• 硬间隔SVM与感知机的区别：
  SVM分类超平面的解是唯一的，要满足间隔最大化；感知机的分类超平面不唯一，没有间隔最大化的约束条件，容易造成过拟合。
• 软间隔SVM与LR的区别：
  （1）LR通过输出预测概率后根据阈值进行判断类别；SVM则直接输出分割超平面，然后使用0/1函数对距离进行分类，不能直接输出概率值。如果需要SVM输出概率值则需要进行特殊处理，可以根据距离的大小进行归一化概率输出。
  （2）LR采用交叉熵损失(CE loss)，SVM采用合页/铰链损失(hinge loss)。SVM自带了正则化项，是结构风险最小化算法，而LR需要另外在损失函数上添加正则项。
  （3）LR对异常值敏感；SVM对异常值不敏感，泛华能力强，分类效果好。
  （4）SVM在训练过程只需要支持向量的数据，依赖的训练样本数较小；而LR则是需要全部的训练样本数据，在训练时开销更大。
  （5）LR可以使用多阈值然后进行多分类，SVM则需要进行推广。

总结

  上述是一些基础的机器学习算法，虽然目前在深度学习中的应用不是很多，但是弄清楚其中的发展脉络和关联也是有必要的。目前，国内工业界应用机器学习较多的领域主要包括：金融、媒体、零售、能源、政府、医疗和算力等。像金融、媒体、零售的用户较多，满足机器学习建模对数据量的要求，而且有大量可以使用机器学习建模的场景。比如，金融领域反欺诈的分类任务使用了GBDT和LR，为用户推荐理财产品等营销场景（类似的，媒体及零售领域推荐浏览过感兴趣的相关内容）都使用推荐算法（协同过滤算法）。而目前工业界最火的机器学习研究方向是AutoML(自动机器学习)技术，这也是未来发展的一个趋势。深度学习主要是应用在CV(计算机视觉)和NLP(自然语言处理)，与机器学习的区别在于其特征的可解释性较差、算力开销大。