STL——heap（heap并不属于STL容器组件）C++实现

heap并不归属于STL容器组件，它是个幕后英雄，扮演priority queue的助手，priority queue允许用户以任何次序将任何元素放入容器内，但是取出时一定是从优先级最高的元素开始取，heap正是具有这样的特性，适合作为priority queue的底层机制

heap的四种算法：push_heap、pop_heap、sort_heap、make_heap，对应插入、删除、排序、建堆， 下述算法理解都以大顶堆为例

由于堆是一棵完全二叉树，所以可以很轻易地用一个数组存储堆中的每一个元素，并且由子结点访问到其父亲结点和由父亲结点访问到其子结点。下面给出图来说明该表示方法：

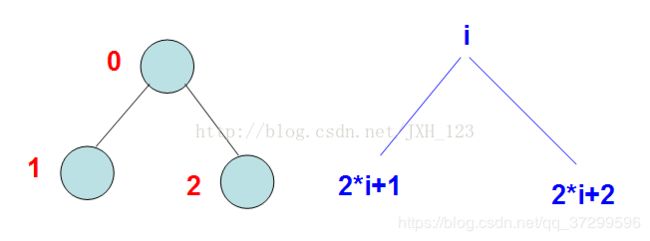
数据结构上heap的实现

STL的魅力之一在于能够对特定类型的数据结构提供泛型化，并且提供高效的函数接口。STL不仅实现了heap算法，而且还弥补上述算法的不足。
平时的heap算法都是针对一个静态数组，而STL以动态数组vector为底层实现，但提供的依旧是建堆操作、插入操作、删除操作、堆排序操作

//底层用静态数组实现的heap

#include
#include
#define maxn 1001   //heap's size

using namespace std;

struct Heap {
	int size;	// number of elements in array
	int *array;
	Heap() {	//初始化
		size = 0;
		array = new int[maxn];
	}
	Heap(int n) {	//init
		size = 0;
		array = new int[n];
	}
	~Heap() {	//free memory
		delete array;
	}
	bool empty() {
		if(size != 0) return false;
		return true;
	}
	
	int max() {
		if(empty()) return -1;
		return array[1];
	}
};

而STL底层用vector实现

#include
#include
#include//有heap算法
using namespace std;
int main()
{
	int ia[9] = {0,1,2,3,4,5,6,7,8,9};
	vector<int> ivec(ia, ia+9);//底层用vector
	make_heap(ivec.begin(),ivec.end());
	...
	
}

①数组新加入一个元素：先插入在数组的最后一个，在堆上看就是这棵完全二叉树的底层最左边叶子节点，要符合大顶堆，则不断往上比较，如果当前index值大于父节点index/2则交换，

	void insert(int value) {
		array[++size] = value;
		int index = size;
		while(index > 1) {
			if(array[index] > array[index/2]) swap(array[index],array[index/2]);
			index /= 2;
		}
	}

而STL用push_heap算法实现

inline void push_heap(b,e,cmp=greater<T>() )

向堆中插入元素分为两个步骤：
（1）先通过push_back将待插入的元素插入到底层容器的末端
（2）再调用push_heap(b,e,cmp)函数堆新插入的元素做向上调整。

②删除堆顶元素：将最后一个元素放到第一个元素处，再从上到下调整使符合大顶堆要求，

	void del() 
	{
		if(empty()) return;
		swap(array[1],array[size--]);
		int index = 1;
		while(2*index <= size) 
		{
			int next = 2*index;
			if(next < size && array[next+1] > array[next]) next++;//和左右子节点中较大的比较交换
			if(array[index] < array[next]) 
			{
				swap(array[index],array[next]);
				index = next;//交换并往下比较，直到到叶子节点
			} else break;
		}
	}

STL中的堆顶元素删除操作：
堆假删除算法：inline void pop_heap(b,e,cmp=greater() )
要实现堆的真正删除操作，分两步进行：
（1）先调用pop_heap函数将首部的元素与尾部元素交换，再将原尾部的元素做向下调整操作。此时，原堆顶元素被放置在最后一个位置，并未从底层容器中删除。
（2）若要实现真正的元素删除，可以调用底层容器的pop_back函数。
所以，在调用pop_heap函数后，若要实现元素真正从堆中删除，还需要调用底层容器的pop_back函数。

③建堆：对非叶子节点进行进行调整从而得到一个大顶堆

void buildHeap(int array[],int size) {
	int i,tmp,index;
	for(i = size/2; i >= 1; i--) {//对每一个非叶子节点从上到下调整
		tmp = array[i];
		index = 2*i;
		while(index <= size) {//堆化
			if(index < size && array[index+1] > array[index]) index++;
			if(array[index] < tmp) break;
			array[index/2]  = array[index];
			index *= 2;
		}
		array[index/2] = tmp;
	}
}

STL建堆算法：inline void make_heap( b, e , cmp=greater() )
该函数对[b,e)范围中的元素建立一个堆，所建的堆的类型由cmp决定，默认为大顶堆。

④堆排序：获取堆顶元素， 与没排序元素的最后一个交换， 当整个程序执行完毕就会得到一个递增序列

void heapsort(int array[],int size)
{
	buildheap(array, size);//先建堆得到一个合格的堆
	int i = size;
	while(true)
	{
		if(i<=1)
			break;
		swap(array, 1, i);//和最后一个交换
		i--;//始终是未排序的最后一个
		//heapify();再对前面的元素进行堆化
	}
}

STL的堆排序算法：

inline void sort_heap(b,e,cmp=greater<T>() )

堆排序实际上是对堆中元素不断地假删除操作，只不过在删除过程中，[b,e)中的e每删除一次，就要做–e的更新。

小顶堆的测试程序

小顶堆取决于cmp这个仿函数的定义

#include
#include
#include
#include//后面用到copy函数和heap相关函数
#include//后面用到迭代器ostream_iterator
#include//后面用到了一个比较的仿函数greater
using namespace std;

typedef vector<int> Vint;//vector底层
void print(const Vint& vec)//输出当前vector容器中的元素
{
	cout<<"容器内的元素为:";
	copy(vec.begin(),vec.end(),ostream_iterator<int>(cout," "));//将容器内的元素输出到标准输出设备上
	cout<<endl;
	cout<<"容器内元素的个数为:"<<vec.size()<<endl<<endl;;
}
 
bool cmp(const int &a,const int &b)
{
	return a>b;//大顶堆，则cmp相等于greater(),注意不是greater，前者是一个对象，后者是一个类
}
int main()
{
	int arr[]={3,2,1,9,4,12,15,7};
	vector<int>vec(arr,arr+sizeof(arr)/sizeof(int));//创建一个vector容器对象，将数组的副本压入到该容器中
	cout<<"-----------初始状态---------------"<<endl;
	print(vec);//将最初的vector容器的内容输出
 
	cout<<"-------------建堆----------------"<<endl;
	make_heap(vec.begin(),vec.end(),cmp);//新建一个小顶堆
	//⭐⭐上行代码等价于make_heap(vec.begin(),vec.end(),greater()⭐⭐
	print(vec);
	
	cout<<"----------弹出堆顶元素-----------"<<endl;
	pop_heap(vec.begin(),vec.end(),cmp);//这里也要加cmp，因为弹出之后要给出向下调整的规则，否则系统会调用默认的最大堆调整方法
	print(vec);
 
	cout<<"--------向堆中插入值6的方法--------"<<endl;
	vec.push_back(6);//先将待插入的值放在容器的末尾
	push_heap(vec.begin(),vec.end(),cmp);//再最堆进行向下调整
	print(vec);
 
	cout<<"----------执行堆排序--------------"<<endl;
	sort_heap(vec.begin(),vec.end(),cmp);
	print(vec);
	return 0;
}

---

优先队列
需要调动到#include，以下以a为例：
大根堆的调用：priority_queuea;
小根堆的调用：priority_queue,greater > a;

a.size():返回堆内元素个数。
a.empty():如果堆为空，返回真，否则返回假。
a.top():返回堆顶元素。
a.pop():删除堆顶元素，自动整理。
a.push(x):插入一个元素x，自动整理。