《学习javascript数据结构与算法》图

图

• 邻接表 创建（队列+字典）

图是网络结构的抽象模型。图是一组由边连接的节点(或顶点)。学习图是重要的，因为任
何二元关系都可以用图来表示。

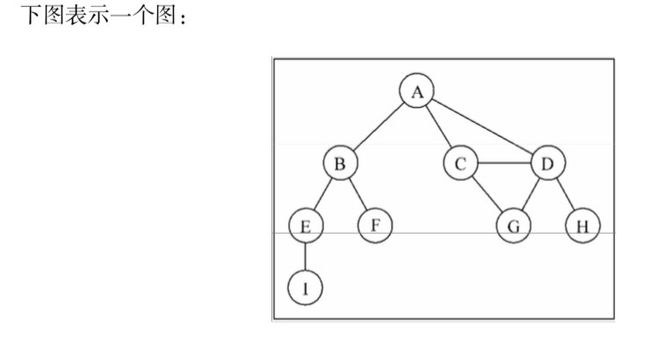
在着手实现算法之前，让我们先了解一下图的一些术语。

术语	解释
相邻顶点	由一条边连接在一起的顶点称为相邻顶点。
度	一个顶点的度是其相邻顶点的数量
路径	路径是顶点v1, v2,…,vk的一个连续序列
环	环也是一个简单路径，比如A D C A(最后一个顶点重新回到A)。

有向图和无向图

图可以是无向的(边没有方向)或是有向的(有向图)。如下图所示，有向图的边有一个方向

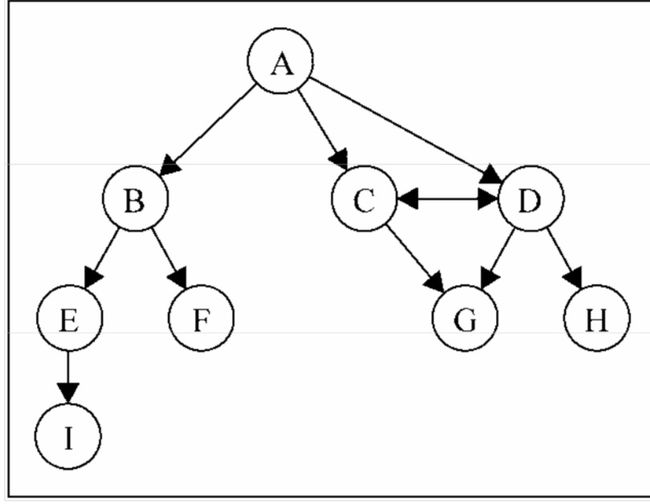
如果图中每两个顶点间在双向上都存在路径，则该图是强连通的。例如，C和D是强连通的，
而A和B不是强连通的。
图还可以是未加权的(目前为止我们看到的图都是未加权的)或是加权的。如下图所示，加
权图的边被赋予了权值:

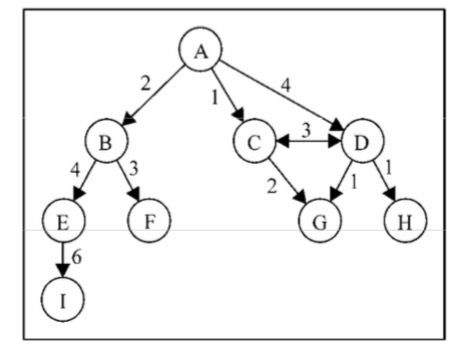
邻接矩阵

图最常见的实现是邻接矩阵。每个节点都和一个整数相关联，该整数将作为数组的索引。我 们用一个二维数组来表示顶点之间的连接。如果索引为i的节点和索引为j的节点相邻，则array[i][j] === 1，否则array[i][j] === 0，如下图所示

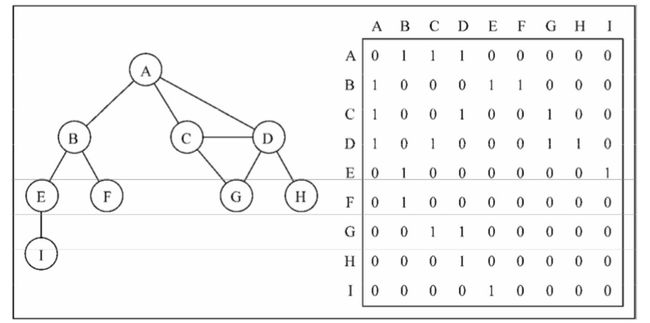
不是强连通的图(稀疏图)如果用邻接矩阵来表示，则矩阵中将会有很多0，这意味着我们 浪费了计算机存储空间来表示根本不存在的边。例如，找给定顶点的相邻顶点，即使该顶点只有 一个相邻顶点，我们也不得不迭代一整行。邻接矩阵表示法不够好的另一个理由是，图中顶点的 数量可能会改变，而2维数组不太灵活

关联矩阵

我们还可以用关联矩阵来表示图。在关联矩阵中，矩阵的行表示顶点，列表示边。如下图所 示，我们使用二维数组来表示两者之间的连通性，如果顶点v是边e的入射点，则array[v][e] === 1; 否则，array[v][e] === 0
关联矩阵通常用于边的数量比顶点多的情况下,以节省空间和内存。

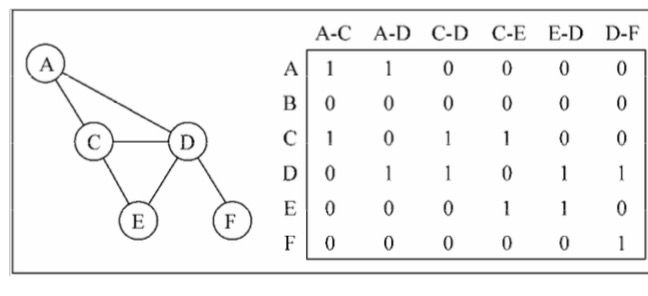
邻接表

我们也可以使用一种叫作邻接表的动态数据结构来表示图。邻接表由图中每个顶点的相邻顶 点列表所组成。存在好几种方式来表示这种数据结构。我们可以用列表(数组)、链表，甚至是 散列表或是字典来表示相邻顶点列表。下面的示意图展示了邻接表数据结构。

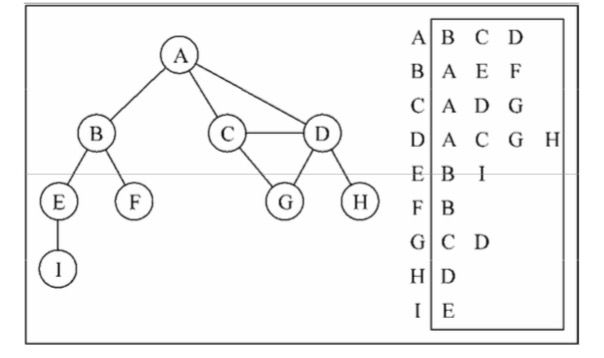
尽管邻接表可能对大多数问题来说都是更好的选择，但以上两种表示法都很有用，且它们有 着不同的性质(例如，要找出顶点v和w是否相邻，使用邻接矩阵会比较快)。我们将会使用邻接表表示法

下面代码实现我们的图
我们的Graph它包括

方法名	解释
addVertex	向图中添加一个新的顶点
addEdge	描边
toString	展现图
bfs	广搜基础实现
BFS	使用BFS寻找最短路径
dfs	深搜

    function Queue(){

        let items = [];

        this.enqueue = function(element){
            items.push(element);
        };

        this.dequeue = function(){
            return items.shift();
        }

        this.front = function(){
            return items[0];
        }

        this.isEmpty = function(){
            return items.length===0;
        }

        this.clear = function(){
            items.length = 0;
        }

        this.size = function(){
            return items.length;
        }

        this.print = function(){
            console.log(items.toString());
        }
    }

    function Dictionary(){

        let items = {};

        this.has = function(key){
            return key in items;
        };

        this.get = function(key){
            return this.has(key)?items[key]:undefined;
        };

        this.set = function(key,value){
            items[key] = value;
        }

        this.remove = function(key){
            if(this.has(key)){
                delete items[key];
                return true;
            }
            return false;
        }

        this.values = function(){
            let result = [];
            for(let key in items){
                if (this.has(key)) {
                    result.push(items[key])
                }
            }
            return result;
        }

        this.getItems = function(){
            return items;
        }
    }
    function Stack() {
        var items = [];
        this.push = function(element){
            items.push(element);
        };
        this.pop = function(){
            return items.pop();
        };
        this.peek = function(){
            return items[items.length-1];
        };
        this.isEmpty = function(){
            return items.length == 0;
        };
        this.size = function(){
            return items.length;
        };
        this.clear = function(){
            items = [];
        };
        this.print = function(){
            console.log(items.toString());
        }
    }
    function Graph() {

        var vertices = []; 
        var adjList = new Dictionary(); 
        // 向图中添加一个新的顶点
        this.addVertex = function(v){
            vertices.push(v); 
            adjList.set(v, []);
        };
        // 描边
        this.addEdge = function(v, w){
            adjList.get(v).push(w); 
            adjList.get(w).push(v); 
        }
        // 展现图
        this.toString = function(){
            let str = "";
            let length = vertices.length;
            for(let i=0;i<length;i++){
                let key = vertices[i];
                str+=`${key}->${adjList.get(key).join(' ')}\n`
            }
            return str;
        }

        var initializeColor = function(){
             var color = [];
            for (var i=0; i< vertices.length; i++){
                color[vertices[i]] = 'white';
            }
            return color;
        }
        // 版本1 会访问所有与其距离为1的顶点，接着是距离为2的顶点
        this.bfs = function(v, callback){
            // debugger;
            var color = initializeColor(),
            queue = new Queue();
            queue.enqueue(v); //A 
            while (!queue.isEmpty()){
               var u = queue.dequeue(),
               neighbors = adjList.get(u); 
               color[u] = 'grey';              
               for(var i=0; i<neighbors.length; i++){
                    var w = neighbors[i];
                    if (color[w] === 'white'){
                        color[w] = 'grey'; 
                        queue.enqueue(w);
                    } 
                }
                color[u] = 'black'; 
                if (callback) {     
                    callback(u);
                }
            }
        }
        // 使用BFS寻找最短路径
        this.BFS = function(v){
            var color = initializeColor(),
            step=[],
            pred=[],
            queue = new Queue();
            queue.enqueue(v);
            let vlength = vertices.length;
            for(let i=0;i<vlength;i++){
                step[vertices[i]]=0;
                pred[vertices[i]] = null;
            }
            while (!queue.isEmpty()){
               var current = queue.dequeue(),
               neighbors = adjList.get(current); 
               color[current] = 'grey';      
               for(var i=0; i<neighbors.length; i++){
                    var child = neighbors[i];

                    // 我们看下 A->I 的过程 要经过A->B->E->I
                    // 首先 neighbors 等于A的队列[ B C D ]的时候 step.B = step.A+1 = 1;
                    // 等来了B的队列[ A ,E ,F]的时候  step.E = step.B+1 = 2;
                    // 最后到了E的队列[  B , I ]的时候  step.I = step.E+1 = 3;

                    if(color[child] === 'white'){
                        color[child] = 'grey'; 
                        step[child] = step[current] + 1; 
                        pred[child] = current;
                        queue.enqueue(child);
                    } 
                }
                color[current] = 'black'; 
            }
            return {
                distances: step, // 从顶点到其他点的步数
                predecessors: pred  // 前溯点，也就是该点的上一个点
            }
        }
        //深搜  
        this.dfs = function(callback){
            var color = initializeColor();
            for (var i=0; i<vertices.length; i++){ 
                if (color[vertices[i]] === 'white'){ 
                    dfsVisit(vertices[i], color, callback);
                }
            } 
        };

        var dfsVisit = function(current, color, callback){
            color[current] = 'grey'; 
            if (callback) { 
                callback(current);
            }
            var neighbors = adjList.get(current);
            for (var i=0; i<neighbors.length; i++){
                var child = neighbors[i];
                if(color[child] === 'white'){
                    dfsVisit(child, color, callback);
                } 
            }
            color[current] = 'black';
        };
        
    }


    var graph = new Graph();

    var myVertices = ['A','B','C','D','E','F','G','H','I'];

    for (var i=0; i<myVertices.length; i++){ 
        graph.addVertex(myVertices[i]);
    }

    graph.addEdge('A', 'B'); 
    graph.addEdge('A', 'C');
    graph.addEdge('A', 'D');
    graph.addEdge('C', 'D');
    graph.addEdge('C', 'G');
    graph.addEdge('D', 'G');
    graph.addEdge('D', 'H');
    graph.addEdge('B', 'E');
    graph.addEdge('B', 'F');
    graph.addEdge('E', 'I');

    // console.log(graph.toString());

    // function printNode(value){
    //     console.log('Visited vertex: ' + value); 
    // }
    // graph.bfs(myVertices[4], printNode);

    var shortestPathA = graph.BFS(myVertices[0]);
    console.log(shortestPathA);

     /*  通过前溯点数组，我们可以构建从顶点A到其他顶点的路径  */
    // 拿到第一个顶点
    var fromVertex = myVertices[0]; 
    // 遍历所有的点
    for (var i=1; i<myVertices.length; i++){ 
        //拿到第二个点
        var toVertex = myVertices[i],
        //创建栈 存储路径值
        path = new Stack(); 
        //接着，追溯toVertex到fromVertex的路径
        for (var v=toVertex; v!== fromVertex;v=shortestPathA.predecessors[v]) { 
            // 将变量v 也就是从远到近的顶点依次添加到栈中
            path.push(v);
        }
        // 将变量v(起点)添加到栈中
        path.push(fromVertex);
        var s = path.pop();
        while (!path.isEmpty()){
            s += ' - ' + path.pop();
            console.log(s);
        }
    }
    // 最终的s就是从起始点到其他顶点的最短路径