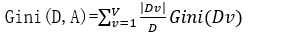决策树算法

决策树的起源：

1、最早的决策树算法是由Hunt等人于1966年提出，Hunt算法是许多决策树算法的基础，包括ID3、C4.5和CART等

2、Hunt算法通过将训练记录相继划分为较纯的子集，以递归方式建立决策树。设Dt是与结点t相关联的训练记录集，而y = { y1, y2, …, yc}为类标号

3、Hunt算法的递归定义如下：

（1）如果Dt中所有的记录都属于同一个类yt，则结点t是叶子结点，用yt标记；

（2）如果Dt中包含多个类的记录，则选择一个属性测试条件，将记录划分为较小的子集。对于测试条件的每个输出，创建一个子女结点，并根据测试结果将Dt中的记录分布到子女结点中，然后对每个子女结点递归地调用该算法；

决策树的概述：

1. 一般，一棵决策树包含一个根节点，若干个内部结点和若干个叶结点；叶结点对应于决策结果，其他每个结点对应于一个属性测试；每个结点包含的样本集合根据属性测试的结果划分到子结点中，根结点包含样本全集，从根结点到每个叶结点的路径对应了一个判定的测试序列。决策树学习的目的是产生一棵泛化能力强，即处理未见示例强的决策树。
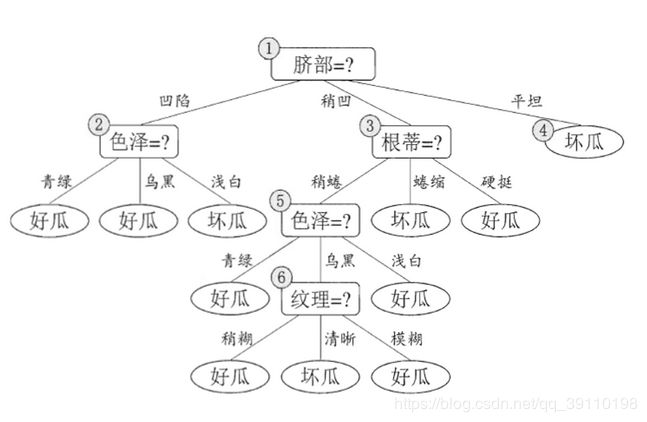
2. 决策树示意图如下:  椭圆-----内部结点即划分属性  方框----叶子节点即分类后的样本
3. 
    

决策树的划分选择

1. 信息增益

        信息熵：当前样本集合D中第k类样本所占的比例为pk

     

        信息熵的值越小，则D的纯度越高

        信息增益：一般而言，信息增益越大，意味着使用属性a来进行划分所获得的 “纯度提升”越大

    

      ID3决策树学习算法就是以信息增益为准则来选择划分属性，信息增益准则对取值数目较多的属性有所偏好

 

     2.增益率

        增益率定义如下：

     

        其中：

     

    C4.5决策树算法采用的即是增益率，增益率准则一般对可取值数目较少的属性有所偏好，故一般不直接选用增益率最大的为    候选划分属性，而是先从候选的划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的

 

  3.基尼指数

    数据集D的纯度可用基尼值来度量

           

      (pk:数据集D中，第k类样本所占的概率)

      Gini(D)越小，数据集D的纯度越高

      数据集D在属性A条件下的基尼指数计算如下：

     

     CART决策树采用的是基尼指数来选择最优属性。在候选属性集合A中，选择那个使得划分后基尼指数最小的属性为最优划分  属性

决策树算法

      决策树伪代码

      决策树示意图

决策树的优化----剪枝

剪枝是决策树学习算法对付“过拟合”的主要手段，决策树剪枝的基本策略有“预剪枝”和“后剪枝”

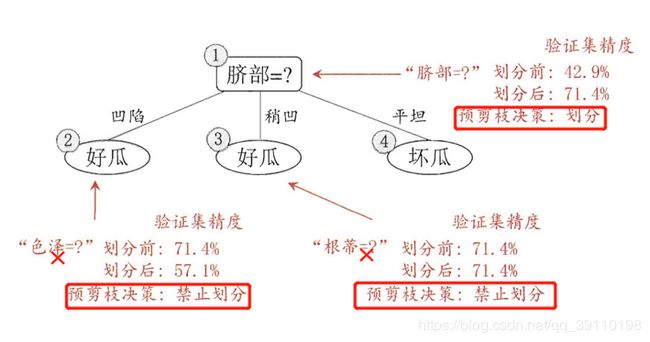
预剪枝：是指在决策树生成过程中，对每个结点在划分前先进行估计，若在当前结点划分不会带来决策树的泛化性能提升，则停止划分，并将当前结点标记为叶结点

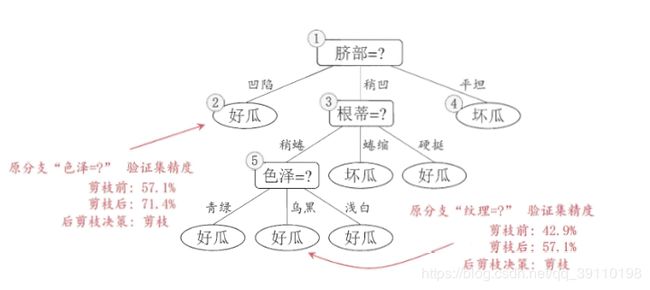
后剪枝：是先从训练集生成一棵完整的决策树，然后自底向上对非叶子结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树的提升，则将子树替换为叶结点

 

 

 

 

 

 

 

 

 

 

预剪枝与后剪枝的比较：

后剪枝决策树通常比预剪枝决策树保留了更多的分支。一般情况下,后剪枝决策树的欠拟合风险很小,泛化性能往往由于预剪枝决策树,但是后剪枝过程是在生成完全决策树后进行的,并且要自下往上地对树中的非叶子节点逐一进行考察计算,因此训练时间的开销比为剪枝和预剪枝决策树都要大得多

决策树的优缺点

优点:
(1)速度快: 计算量相对较小, 且容易转化成分类规则. 只要沿着树根向下一直走到叶, 沿途的分裂条件就能够唯一确定一条分类的谓词.
(2)准确性高: 挖掘出来的分类规则准确性高, 便于理解, 即可以生成可以理解的规则.
(3)可以处理连续和离散字段
(4)不需要任何领域知识和参数假设
(5)适合高维数据

缺点:
(1)对于各类别样本数量不一致的数据, 信息增益偏向于那些更多数值的特征

(2)容易过拟合
(3)忽略属性之间的相关性

 

随机森林

1. 随机森林（Random Forest,简称RF）是Bagging的一个扩展变体，RF在以决策树为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入了随机属性选择
2. 什么是随机森林
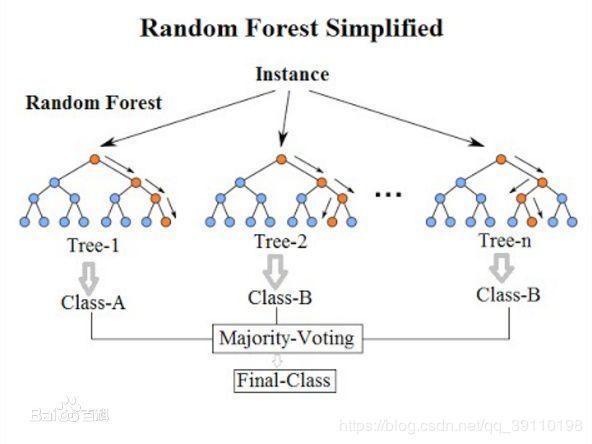
3. 随机森林分解开来就是“随机”和“森林”。“随机”即随机抽样以及随机属性选择；森林是由很多棵树组成的，因此随机森林的结果是依赖于多棵决策树的结果，这是一种集成学习的思想。森林里新来了一只动物，森林举办森林大会，判断这到底是什么动物，每棵树都必须发表意见，票数最多的结果将是最终的结果。随机森林最终的模型见下图示：

 

随机森林基本思想

1、有放回的随机采样(自助采样法 西瓜书2.2.3节)

给定包含m个样本的数据集（初始训练集），有放回的随机抽取m次样本，得到m个样本采样集，初始训练集约有63.2%的数据出现在采样集中

2、随机属性选择

对基决策树的每个结点，先从该结点的属性集合(d个属性)中随机选择一个包含k个属性的子集，然后再从这个子集中选择一个最

优属性用于划分；参数k控制了随机性引入程度；一般情况下，推荐值或者

随机森林中基学习器的多样性不仅来自于样本扰动，还来自属性扰动，使得最 终集成的泛化性能可通过个体学习器之间的差异度的增加进一步提升

随机抽样以及特征提取图示:

 

随机森林模型图示：

随机森林实现伪代码：

1、获取数据集D

2、初始化随机森林分类器中各个参数

3、建立随机森林

①随机抽取m个训练样本

②利用训练样本建树，划分特征选取的方式为对于某一结点先随机选择k个特征，再从k个特征中选择最优划分特征，以此规则建树

③将建立的树放入集成池中，直至达到规定池的大小

随机森林特点：

1. 在当前所有算法中，具有极好的准确率
2. 能够有效地运行在大数据集上
3. 能够处理具有高维特征的输入样本，而且不需要降维
4. 能够评估各个特征在分类问题上的重要性
5. 在生成过程中，能够获取到内部生成误差的一种无偏估计