PointNet:Deep Learining on Point Sets for 3D Classification and Segmentation 论文解析
一. Abstract
二.Introduction
三.Related Work
四.Deep Learning on Point Sets
五.Theoretical Analysis
六.Experiment
一.Abstract
1.首先点云是一种重要几何数据结构的类型。
2.以往处理点云的方法:
鉴于点云的不规则形式可以将点云转换为3D体素网格或者图片集。
3.存在的缺点:
造成大量的数据冗余以及造成很多其他问题。
4.PointNet:
(1)直接使用点云(x,y,z)进行物体分类、部分分割,场景分割。
(2)PointNet是高效高性能的。
(3)对于噪音和数据污染有很强的鲁棒性。
一.Introduction
1.卷积要求输入数据形式的高度规则性为了实现权重共享以及其他的核优化,像图片网格以及3D体素。
2.点云网络是简单和统一结构,这样避免不规则和复杂的网格因此更容易进行学习。
3.PointNet是一个统一的体系结构,它直接将点云作为输入并输出整个输入的标签,或输入的每个点的每个点段/部件标签。在基本设置中,每个点都由它的三个坐标(x,y,z)表示。额外的维度可以通过计算法线和其他局部或全局特性来添加。
4.点云输入格式很容易应用刚性或仿射转换,因为每个点独立转换。因此,我们可以添加T-Net,它在处理数据之前对数据进行规范化,从而进一步改进结果
5.网络学会了用一组稀疏的关键点来概括一个输入点云,根据可视化,这些关键点大致对应于对象的骨架。提供了抗干扰能力,下图是可视化后的结果,可以看出一小块都是一个物体的骨架

6.本文的贡献:
(1)pointnet可以直接处理无规则的3D点云数据
(2)pointnet可以被训练用来进行分类,部分分割和场景语义分割
(3)对该方法的稳定性和有效性进行了深入的实证和理论分析
(4)举例说明了由网络中选定的神经元计算出的三维特征,并对其性能做出了直观的解释
三.Related Work
1.Deep Learning on 3D Data
(1)3D CNN应用于3D 数据中,然而体积表示被分辨率所限制由于数据稀疏, 3D卷积的计算消耗
(2)multiview CNNS:3D点云----Projection------2D图像-----conv------分类,该方法在形状分类和检索任务中取得了优异的性能。
(3)Spectral CNNs(光谱):应用在有机物,目前没有扩展到无机物物体上。
(4)Feature-based DNNs:首先将三维数据转换为矢量,提取形状特征,然后利用全连接网络对形状进行分类。
四.Deep Learning on Point Sets
1.无序性:与图像中的像素阵列或体素阵列不同,点云是一组没有特定顺序的点
2.点之间的交互:这些点来自一个距离度量的空间。这意味着点不是孤立的,相邻的点构成一个有意义的子集。因此,该模型需要能够从附近的点捕获局部结构,以及局部结构之间的组合交互。
3.平移不变性:作为一个几何对象,点集的学习表示应该不受某些变换的影响。例如,所有旋转和平移点都不应该修改全局点云类别或点的分割。
点云架构
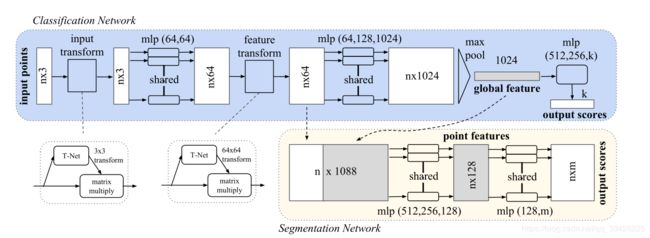 1.解决点云的无序性:
1.解决点云的无序性:
(1)每次进来点云都按一定规则去进行排序
(2)训练RNN使得每个点之间都有关联
(3)使用对称函数来聚集信息
Q:什么是对称函数 ?
A:输入n个向量,输出一个向量,输出向量不受输入向量的顺序影响。
缺点:(1)每次点云都进行排序浪费时间和提高了计算成本
(2)大规模数据的RNN网络太过复杂,精度变低并且难以训练
五.Theoretical Analysis
1. 首先证明了神经网络对连续集函数的普遍逼近能力
2.Hausdorff distance:
Hausdorff距离是描述两组点集之间相似程度的一种量度,它是两个点集之间距离的一种定义形式:假设有两组集合A={a1,…,ap},B={b1,…,bq},则这两个点集合之间的Hausdorff距离定义为
H(A,B)=max(h(A,B),h(B,A)) (1)
其中,
h(A,B)=max(a∈A)min(b∈B)‖a-b‖ (2)
h(B,A)=max(b∈B)min(a∈A)‖b-a‖ (3)
‖·‖是点集A和B点集间的距离范式(如:L2或Euclidean距离).
这里,式(1)称为双向Hausdorff距离,是Hausdorff距离的最基本形式;式(2)中的h(A,B)和h(B,A)分别称为从A集合到B集合和从B集合到A集合的单向Hausdorff距离.即h(A,B)实际上首先对点集A中的每个点ai到距离此点ai最近的B集合中点bj之间的距离‖ai-bj‖进行排序,然后取该距离中的最大值作为h(A,B)的值.h(B,A)同理可得.
由式(1)知,双向Hausdorff距离H(A,B)是单向距离h(A,B)和h(B,A)两者中的较大者,它度量了两个点集间的最大不匹配程度.

3.解释一下:这是为了证明网络的拟合,当从S, S , S^, S,取任何值时,他们的豪斯道夫距离小于 σ \sigma σ,并且连续函数f(S)-f( S , S^, S,)小于 ϵ \epsilon ϵ时
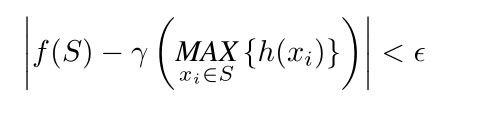
如果mlp能够满足精度则说明该网络可以拟合,其中h(),y()表示mlp,MAX代表maxpooling。
