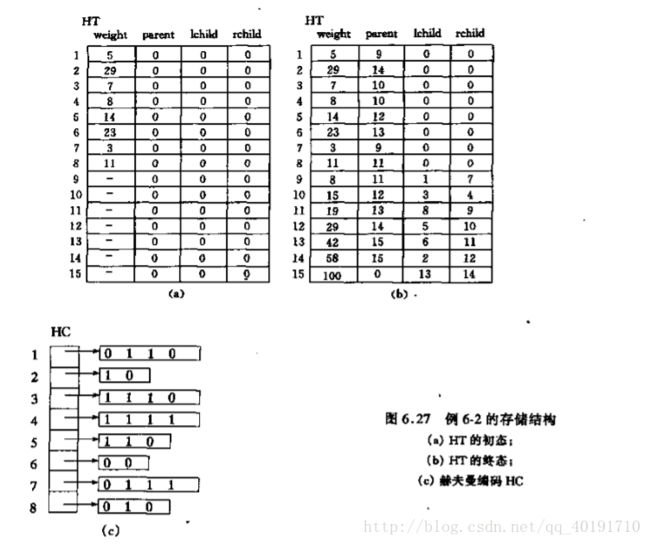
第六章-树（6）赫夫曼树

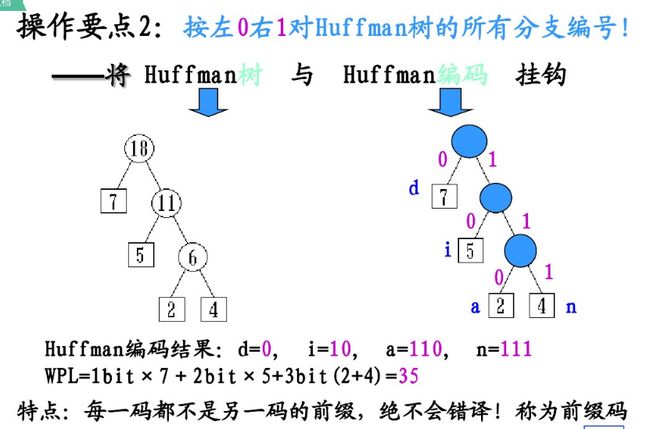
赫夫曼编码的基本思想是：概率大的字符用短码，概率小的用长码。

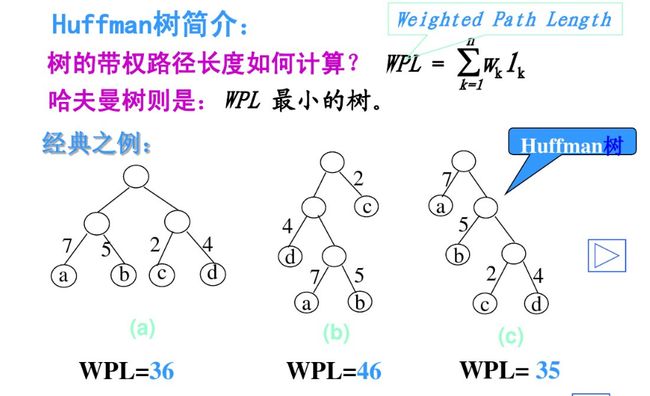
                                      由于赫夫曼树的WPL最小，说明编码所需的比特数最小。

                                      这种编码已经广泛应用于网络通信中。 

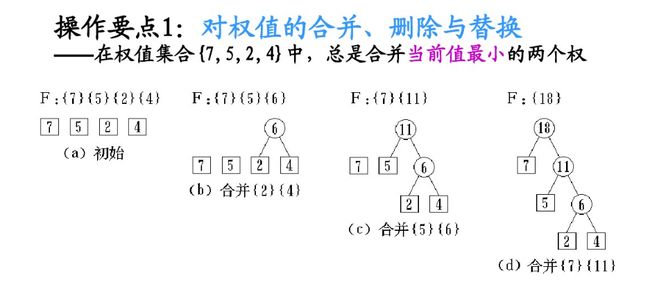
构建赫夫曼树和赫夫曼编码：

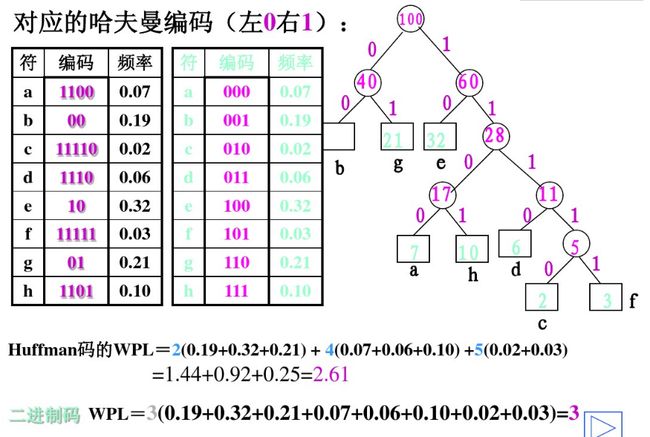
出现的字符：

',','a','b','c','d','e','f','g','h','i','g','k','l','m','n','o','p','q','4','r','s','t','u','v','w','x','y','z'

字符出现的概率：

 187,64,13,22,32,103,21,15,47,57,1,5,32,20,57,63,15,1,48,51,80,23,8,13,1,16,1

    构建赫夫曼树和赫夫曼编码的方法：

--------------------------------------------------------------------------------------------------------------------------------

//设字符集为26个英文字符，其出现频度如下表所示，要求编程实现

#include
#include
#define MaxValue 10000
#define MaxBit 10
#define MaxN 100

typedef struct{   //赫夫曼树的结点结构
	int weight;
	int flag;
	int parent;
	int lchild;
	int rchild;
}HTNode,*HuffmanTree;

typedef struct{
	unsigned int bit[MaxN];
	int strat;
	int weight;
}Code;

//构造赫夫曼树的算法
void HuffmanCoding(int weight[],int n,HTNode HT[]){
	int i,j,m1,m2,x1,x2;
	if(n<=1) return;
	for(i=0;i<2*n-1;i++){              //初始化每一个结点的值
		if(istrat=n-1;
		cd->weight=HT[i].parent;
		child=i;
		parent=HT[child].parent;
		while(parent!=-1){
			if(HT[parent].lchild==child)
				cd->bit[cd->strat]=0;
			else
				cd->bit[cd->strat]=1;
			cd->strat--;
			child=parent;
			parent=HT[child].parent;
		}
		for(j=cd->strat+1;jbit[j];
		HTCode[i].strat=cd->strat+1;
		HTCode[i].weight=cd->weight;
	}
}

void main(){
	int i,j,k,n=27;
	char s[]={',','a','b','c','d','e','f','g','h','i','g','k','l','m','n','o','p','q','4','r','s','t','u','v','w','x','y','z'};
	int weight[]={187,64,13,22,32,103,21,15,47,57,1,5,32,20,57,63,15,1,48,51,80,23,8,13,1,16,1};
    HTNode *myHaffTree=(HTNode *)malloc(sizeof(HTNode)*(2*n+1));
	Code *myHaffCode=(Code *)malloc(sizeof(Code)*n);
	if(n>MaxN)
	{
		printf("给出 n 越界，修改McxN");
		exit(0);
	}
	HuffmanCoding(weight,n,myHaffTree);
	HaffCode(myHaffTree,n,myHaffCode);
	for(i=0;i

编码的方法有两种，一种是从叶子到根，一种是从根到叶。

与编码与之对应的就是译码了。

      赫夫曼树编码的设计过程：                

                       

代码转自他人，只供交流学习。