Palabos 源码学习 | 浸入边界法Immersed Boundary Method

源码中单独的浸入边界法类

首先我们需要了解ib-lbm计算中，先（首次需initial）计算Lagrangian点的力g，再将g spreading on Eulerian格点，接下来执行碰撞和流动，然后通过interpolation得到Lagrangian的速度，最后更新Lagrangian格点位置。
中英穿插的描述是因为方便读者理解论文中用到的英语。

迭代过程中边界力的计算

> template<typename T> void
> ComputeImmersedBoundaryForce3D<T>::processGenericBlocks (
>         Box3D domain, std::vector<AtomicBlock3D*> blocks ) {
>     PLB_PRECONDITION( blocks.size()==2 );
>     TensorField3D<T,3>* force = dynamic_cast<TensorField3D<T,3>*>(blocks[0]);
>     AtomicContainerBlock3D* container = dynamic_cast<AtomicContainerBlock3D*>(blocks[1]);
>     PLB_ASSERT(force);
>     PLB_ASSERT(container);
>     Dot3D location = force->getLocation();
>     ImmersedWallData3D<T>* wallData = 
>         dynamic_cast<ImmersedWallData3D<T>*>( container->getData() );
>     PLB_ASSERT(wallData);
>     std::vector< Array<T,3> > const& vertices = wallData->vertices;
>     std::vector<Array<T,3> >& g = wallData->g;
>     PLB_ASSERT( vertices.size()==g.size() );
> 
>     for (plint iX = 0; iX < force->getNx(); iX++) {
>         for (plint iY = 0; iY < force->getNy(); iY++) {
>             for (plint iZ = 0; iZ < force->getNz(); iZ++) {
>                 force->get(iX, iY, iZ).resetToZero();
>             }
>         }
>     }
> 
>     for (pluint i=0; i<vertices.size(); ++i) {
>         Array<T,3> const& vertex = vertices[i];
>         Array<plint,3> intPos((plint) vertex[0] - location.x, (plint) vertex[1] - location.y, (plint) vertex[2] - location.z);
>         const Array<plint,2> xLim((vertex[0] < (T) 0 ? Array<plint,2>(-2, 1) : Array<plint,2>(-1, 2)));
>         const Array<plint,2> yLim((vertex[1] < (T) 0 ? Array<plint,2>(-2, 1) : Array<plint,2>(-1, 2)));
>         const Array<plint,2> zLim((vertex[2] < (T) 0 ? Array<plint,2>(-2, 1) : Array<plint,2>(-1, 2)));
>         const Array<T,3> fracPos(util::frac(vertex[0]), util::frac(vertex[1]), util::frac(vertex[2]));
>         for (plint dx = xLim[0]; dx <= xLim[1]; dx++) {
>             for (plint dy = yLim[0]; dy <= yLim[1]; dy++) {
>                 for (plint dz = zLim[0]; dz <= zLim[1]; dz++) {
>                     Array<plint,3> pos(intPos+Array<plint,3>(dx,dy,dz));
>                     Array<T,3> r((T)dx-fracPos[0],(T)dy-fracPos[1],(T)dz-fracPos[2]);
>                     T W = inamuroDeltaFunction<T>().W(r);
>                     force->get(pos[0], pos[1], pos[2]) += W*g[i];
>                 }
>             }
>         }
>     } }

主要思路是以张量场的方式收集和计算区块的力。在IBM实现中，已定义rhobar，j，和container，定义的g即为力。

定义force为3D的张量场，定义location为force的位置，定义wallData为container里数据，定义vertices为wallData里的顶点数据（即流域内固体顶点位置），定义g为wallData里的力。

force是基于Eulerian mesh，而g基于Lagrangian mesh。

目测这个force就是作用在eulerian网格上的力，location也是eulerian网格坐标，vertices的顶点坐标vertex和力g都是lagragian网格上的参数。

> template<typename T> struct ImmersedWallData3D : public
> ContainerBlockData {
>     std::vector< Array<T,3> > vertices;
>     std::vector<T> areas;
>     std::vector< Array<T,3> > normals;
>     std::vector< Array<T,3> > g;
>     std::vector<int> flags; // Flag for each vertex used to distinguish between vertices for conditional reduction operations.
>     std::vector<pluint> globalVertexIds;
>     virtual ImmersedWallData3D<T>* clone() const {
>         return new ImmersedWallData3D<T>(*this);
>     } };

循环的第一步将force重置为0，此处我猜测是否了避免整个计算过程中力的累加。

第二个循环则依次在每个顶点上计算。并定义vertex为单个顶点，该顶点由0,1，2表示三个轴坐标。

<表达式1>?<表达式2>:<表达式3> ;

若表达式1为真，则执行表达式2；若表达式1的值为假，则执行表达式3。所以xLim，yLim，zLim的结果只有两种:

1. xLim[0]为-2，xLim[1]为1。
2. xLim[0]为-1，xLim[1]为2。

循环中的dx也是从-2，-1,0，1,2或者-1,0,1,2,3循环。

Array intPos((plint) vertex[0] - location.x, (plint) vertex[1] - location.y, (plint) vertex[2] - location.z);这段代码的作用是得到vertex的Lagrangian坐标，再四舍五入，减去location坐标，intPos得到值是Eulerian坐标，根据IBM作用邻域的概念判断，后续是为了确定计算邻域。

像dx-fracPos[0]即计算Dirac函数中的x方向距离。

Array pos(intPos+Array(dx,dy,dz));dx，dy，dz用于得到周围邻域被施加力的格点Eulerian坐标，由负到正，实际效果则是在这些Eulerian格点pos上作用。

force->get(pos[0], pos[1], pos[2]) += W*g[i];主要是实现下图的g的迭代累加（这里的g是Eulerian点的力）。

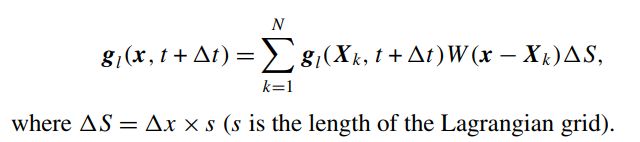
梳理一遍

1）得到Eulerian的force，得到边界Lagrangian坐标
2）利用整型四舍五入拉格朗日坐标来获得欧拉坐标，intPos=(plint) vertex[0] - location.x
3）确定邻域范围，利用pos(intPos+Array(dx,dy,dz))得到周围的欧拉坐标点
4）util::frac(vertex[0]得到小数值，(T)dx-fracPos[0]即计算距离r
5）计算得到体积力force->get(pos[0], pos[1], pos[2]) += W*g[i]

补档

文上几处我猜测的地方还未确定，等确定后会回来修改。

浸入边界的生成

> template<typename T>
> InstantiateImmersedWallData3D<T>::InstantiateImmersedWallData3D (//可见这里需要三个输入参数，其中最后一个是normals
>             std::vector< Array<T,3> > const& vertices_,
>             std::vector<T> const& areas_,
>             std::vector< Array<T,3> > const& normals_)//这个是算例中出现的container
>     : vertices(vertices_),
>       areas(areas_),
>       normals(normals_) {
>     PLB_ASSERT(vertices.size() == areas.size());
>     PLB_ASSERT(normals.size()==0 || normals.size() == areas.size()); }
// 这个rhobar来源于生成标量场
//		MultiScalarField3D *rhoBar = generateMultiScalarField((MultiBlock3D&) *lattice, 
//		largeEnvelopeWidth).release();
//    	rhoBar->toggleInternalStatistics(false);
//container以rhoBar生成
//		MultiContainerBlock3D container(*rhoBar);
> template<typename T> void
> InstantiateImmersedWallData3D<T>::processGenericBlocks (
>         Box3D domain, std::vector<AtomicBlock3D*> blocks ) {
>     PLB_PRECONDITION( blocks.size()==1 );
>     AtomicContainerBlock3D* container = dynamic_cast<AtomicContainerBlock3D*>(blocks[0]);
>     PLB_ASSERT( container );
>     bool useNormals = normals.size()>0;//normals中大于0处定义为1
>     Dot3D location = container->getLocation();
>     ImmersedWallData3D<T>* wallData = new ImmersedWallData3D<T>;//此处定义了wallData
>     Box3D extendedEnvelope(domain.enlarge(2).shift(location.x, location.y, location.z));
> 
>     for (pluint i=0; i<vertices.size(); ++i) {
>         // Vertices which are close to the boundaries of the extendedEnvelope
>         // are irrelevant, because they will act upon the bulk of the computational
>         // domain through an Inamuro kernel, which at this distance is close to zero.
>         // It is therefore OK, numerically speaking to exclude an epsilon-margin close
>         // to these boundaries. Plus, it is required for technical reasons, because if
>         // later on we pass across the boundaries of the extendedEnvelope because
>         // of roundoff errors, the code will crash.
>         static const T epsilon = 1.e-4;
>         if (contained(vertices[i], extendedEnvelope, epsilon)) {
>             wallData->vertices.push_back(vertices[i]);//将顶点数据读入wallData
>             wallData->areas.push_back(areas[i]);//将面积数据读入wallData
>             if (useNormals) {//这样的判断将wallData中的normals里大于0的部分读入wallData
>                 wallData->normals.push_back(normals[i]);
>             }
>             wallData->g.push_back(Array<T,3>((T)0.,(T)0.,(T)0.));//可见初始边界时，其力为0
>             wallData->globalVertexIds.push_back(i);
>         }
>     }
>     wallData->flags = std::vector<int>(wallData->vertices.size(), 0);
>     container->setData(wallData); }//container得到wallData的数据
> 
> template<typename T> InstantiateImmersedWallData3D<T>*
> InstantiateImmersedWallData3D<T>::clone() const {
>     return new InstantiateImmersedWallData3D<T>(*this); }
> 
> template<typename T> void
> InstantiateImmersedWallData3D<T>::getTypeOfModification(std::vector<modif::ModifT>&
> modified) const {
>     modified[0] = modif::staticVariables;  // Container Block with triangle data. }
> 
> template<typename T> BlockDomain::DomainT
> InstantiateImmersedWallData3D<T>::appliesTo() const {
>     return BlockDomain::bulk; }

ImmersedWallData3D

在初始化浸入的边界时，用到了ImmersedWallData3D* wallData = new ImmersedWallData3D;，大体作用是定义了vertices，areas，normals，g，id和flag。

> template<typename T> struct ImmersedWallData3D : public
> ContainerBlockData {
>     std::vector< Array<T,3> > vertices;
>     std::vector<T> areas;
>     std::vector< Array<T,3> > normals;
>     std::vector< Array<T,3> > g;
>     std::vector<int> flags; // Flag for each vertex used to distinguish between vertices for conditional reduction operations.
>     std::vector<pluint> globalVertexIds;
>     virtual ImmersedWallData3D<T>* clone() const {
>         return new ImmersedWallData3D<T>(*this);
>     } };

Inamuro IBM

在palabos中，Inamuro的算法也包含了全套g和j计算。

Inamuro IBM的调用

调用算例取材于MovingWall。

> int ibIter;  param.ibIter = 4;

> instantiateImmersedWallData(vertices, areas, container);
>         for (int i = 0; i < param.ibIter; i++) {
>             inamuroIteration(SurfaceVelocity(timeLB),
>                     *rhoBar, *j, container, (T) 1.0 / param.omega, incompressibleModel);
>         }
>     }

Inamuro迭代

> template<typename T, class VelFunction> class InamuroIteration3D :
> public BoxProcessingFunctional3D { public:
>     InamuroIteration3D(VelFunction velFunction_, T tau_, bool incompressibleModel_);
>     virtual void processGenericBlocks(Box3D domain, std::vector<AtomicBlock3D*> fields);
>     virtual InamuroIteration3D<T,VelFunction>* clone() const;
>     virtual void getTypeOfModification(std::vector<modif::ModifT>& modified) const;
>     virtual BlockDomain::DomainT appliesTo() const; private:
>     VelFunction velFunction;
>     T tau;
>     bool incompressibleModel; };
> 
> template<typename T, class VelFunction> void inamuroIteration (
>     VelFunction velFunction,
>     MultiScalarField3D<T>& rhoBar,
>     MultiTensorField3D<T,3>& j,
>     MultiContainerBlock3D& container, T tau,
>     bool incompressibleModel ) {
>     std::vector<MultiBlock3D*> args;
>     args.push_back(&rhoBar);
>     args.push_back(&j);
>     args.push_back(&container);
>     applyProcessingFunctional (//利用args引用存储一下数据
>         new InamuroIteration3D<T,VelFunction>(velFunction, tau, incompressibleModel), rhoBar.getBoundingBox(), args ); }

> template<typename T, class VelFunction>
> InamuroIteration3D<T,VelFunction>::InamuroIteration3D(VelFunction
> velFunction_, T tau_, bool incompressibleModel_)
>     : velFunction(velFunction_),//velFunction在movingwall算例里有算例体现
>       tau(tau_),
>       incompressibleModel(incompressibleModel_) { }
> 
> template<typename T, class VelFunction> void
> InamuroIteration3D<T,VelFunction>::processGenericBlocks (
>         Box3D domain, std::vector<AtomicBlock3D*> blocks ) {
>     PLB_PRECONDITION( blocks.size()==3 );
>     ScalarField3D<T>* rhoBar = dynamic_cast<ScalarField3D<T>*>(blocks[0]);
>     TensorField3D<T,3>* j = dynamic_cast<TensorField3D<T,3>*>(blocks[1]);
>     AtomicContainerBlock3D* container = dynamic_cast<AtomicContainerBlock3D*>(blocks[2]);
>     PLB_ASSERT( rhoBar );
>     PLB_ASSERT( j );
>     PLB_ASSERT( container );
>     Dot3D location = rhoBar->getLocation();
>     Dot3D ofsJ = computeRelativeDisplacement(*rhoBar, *j);//这里的ofsJ顾名思义，计算了相对变化量，用于后续动量计算
>     ImmersedWallData3D<T>* wallData = 
>         dynamic_cast<ImmersedWallData3D<T>*>( container->getData() );
>     PLB_ASSERT(wallData);//这部分与上文提到的wallData作用相同
> 
>     std::vector< Array<T,3> > const& vertices = wallData->vertices;
>     std::vector<T> const& areas = wallData->areas;
>     PLB_ASSERT( vertices.size()==areas.size() );
>     std::vector<Array<T,3> > deltaG(vertices.size());
>     std::vector<Array<T,3> >& g = wallData->g;
>     PLB_ASSERT( vertices.size()==g.size() );
> 
>     // In this iteration, the force is computed for every vertex.
>     if (incompressibleModel) {
>         for (pluint i=0; i<vertices.size(); ++i) {
>             Array<T,3> const& vertex = vertices[i];
>             Array<plint,3> intPos((plint) vertex[0] - location.x, (plint) vertex[1] - location.y, (plint) vertex[2] - location.z);//int来整型四舍五入取得整数位置，从而以Lagrangian点坐标得到Eulerian点坐标
>             const Array<plint,2> xLim((vertex[0] < (T) 0 ? Array<plint,2>(-2, 1) : Array<plint,2>(-1, 2)));
>             const Array<plint,2> yLim((vertex[1] < (T) 0 ? Array<plint,2>(-2, 1) : Array<plint,2>(-1, 2)));
>             const Array<plint,2> zLim((vertex[2] < (T) 0 ? Array<plint,2>(-2, 1) : Array<plint,2>(-1, 2)));
>             const Array<T,3> fracPos(util::frac(vertex[0]), util::frac(vertex[1]), util::frac(vertex[2]));//得到小数部分
>             Array<T,3> averageJ; averageJ.resetToZero();
>             // Use the weighting function to compute the average momentum
>             // and the average density on the surface vertex.
>             // x   x . x   x
>             for (plint dx = xLim[0]; dx <= xLim[1]; dx++) {
>                 for (plint dy = yLim[0]; dy <= yLim[1]; dy++) {
>                     for (plint dz = zLim[0]; dz <= zLim[1]; dz++) {
>                         Array<plint,3> pos(intPos+Array<plint,3>(dx,dy,dz));//得到周围点坐标
>                         Array<T,3> nextJ = j->get(pos[0]+ofsJ.x, pos[1]+ofsJ.y, pos[2]+ofsJ.z);//nextJ即下一个j的位置
>                         Array<T,3> r((T)dx-fracPos[0],(T)dy-fracPos[1],(T)dz-fracPos[2]);//得出距离r
>                         T W = inamuroDeltaFunction<T>().W(r);// Dirac function，在immersedwall.h最上面就能看到
>                         averageJ += W*nextJ;
>                     }
>                 }
>             }
>             //averageJ += (T)0.5*g[i];
>             Array<T,3> wallVelocity = velFunction(vertex);
>             deltaG[i] = areas[i]*(wallVelocity-averageJ);
>             g[i] += deltaG[i];//得到lagrangian点的力
>         }
>     } else { // Compressible model.
>         for (pluint i=0; i<vertices.size(); ++i) {
>             Array<T,3> const& vertex = vertices[i];
>             Array<plint,3> intPos((plint) vertex[0] - location.x, (plint) vertex[1] - location.y, (plint) vertex[2] - location.z);
>             const Array<plint,2> xLim((vertex[0] < (T) 0 ? Array<plint,2>(-2, 1) : Array<plint,2>(-1, 2)));
>             const Array<plint,2> yLim((vertex[1] < (T) 0 ? Array<plint,2>(-2, 1) : Array<plint,2>(-1, 2)));
>             const Array<plint,2> zLim((vertex[2] < (T) 0 ? Array<plint,2>(-2, 1) : Array<plint,2>(-1, 2)));
>             const Array<T,3> fracPos(util::frac(vertex[0]), util::frac(vertex[1]), util::frac(vertex[2]));
>             Array<T,3> averageJ; averageJ.resetToZero();
>             T averageRhoBar = T();
>             // Use the weighting function to compute the average momentum
>             // and the average density on the surface vertex.
>             // x   x . x   x
>             for (plint dx = xLim[0]; dx <= xLim[1]; dx++) {
>                 for (plint dy = yLim[0]; dy <= yLim[1]; dy++) {
>                     for (plint dz = zLim[0]; dz <= zLim[1]; dz++) {
>                         Array<plint,3> pos(intPos+Array<plint,3>(dx,dy,dz));
>                         T nextRhoBar = rhoBar->get(pos[0], pos[1], pos[2]);
>                         Array<T,3> nextJ = j->get(pos[0]+ofsJ.x, pos[1]+ofsJ.y, pos[2]+ofsJ.z);
>                         Array<T,3> r((T)dx-fracPos[0],(T)dy-fracPos[1],(T)dz-fracPos[2]);
>                         T W = inamuroDeltaFunction<T>().W(r);
>                         averageJ += W*nextJ;
>                         averageRhoBar += W*nextRhoBar;
>                     }
>                 }
>             }
>             //averageJ += (T)0.5*g[i];
>             Array<T,3> wallVelocity = velFunction(vertex);
>             deltaG[i] = areas[i]*((averageRhoBar+(T)1.)*wallVelocity-averageJ);
>             //g[i] += deltaG[i];
>             g[i] += deltaG[i]/((T)1.0+averageRhoBar);
>         }
>     }
>     
>     // In this iteration, the force is applied from every vertex to the grid nodes.
>     for (pluint i=0; i<vertices.size(); ++i) {
>         Array<T,3> const& vertex = vertices[i];
>         Array<plint,3> intPos((plint) vertex[0] - location.x, (plint) vertex[1] - location.y, (plint) vertex[2] - location.z);
>         const Array<plint,2> xLim((vertex[0] < (T) 0 ? Array<plint,2>(-2, 1) : Array<plint,2>(-1, 2)));
>         const Array<plint,2> yLim((vertex[1] < (T) 0 ? Array<plint,2>(-2, 1) : Array<plint,2>(-1, 2)));
>         const Array<plint,2> zLim((vertex[2] < (T) 0 ? Array<plint,2>(-2, 1) : Array<plint,2>(-1, 2)));
>         const Array<T,3> fracPos(util::frac(vertex[0]), util::frac(vertex[1]), util::frac(vertex[2]));
>         for (plint dx = xLim[0]; dx <= xLim[1]; dx++) {
>             for (plint dy = yLim[0]; dy <= yLim[1]; dy++) {
>                 for (plint dz = zLim[0]; dz <= zLim[1]; dz++) {
>                     Array<plint,3> pos(intPos+Array<plint,3>(dx,dy,dz));
>                     Array<T,3> nextJ = j->get(pos[0]+ofsJ.x, pos[1]+ofsJ.y, pos[2]+ofsJ.z);
>                     Array<T,3> r((T)dx-fracPos[0],(T)dy-fracPos[1],(T)dz-fracPos[2]);
>                     T W = inamuroDeltaFunction<T>().W(r);
>                     nextJ += tau*W*deltaG[i];
>                     j->get(pos[0]+ofsJ.x, pos[1]+ofsJ.y, pos[2]+ofsJ.z) = nextJ;//同样是得到r，这次是计算g的spreading on Eulerian格点
>                 }
>             }
>         }
>     } }
> 
> template<typename T, class VelFunction>
> InamuroIteration3D<T,VelFunction>*
> InamuroIteration3D<T,VelFunction>::clone() const {
>     return new InamuroIteration3D<T,VelFunction>(*this); }
> 
> template<typename T, class VelFunction> void
> InamuroIteration3D<T,VelFunction>::getTypeOfModification(std::vector<modif::ModifT>&
> modified) const {
>     modified[0] = modif::nothing;          // RhoBar
>     modified[1] = modif::staticVariables;  // J
>     modified[2] = modif::nothing;          // Container Block with triangle data. }
> 
> template<typename T, class VelFunction> BlockDomain::DomainT
> InamuroIteration3D<T,VelFunction>::appliesTo() const {
>     return BlockDomain::bulk; }