数据挖掘基础
数据挖掘基础
数据挖掘就是：
数据挖掘的建模过程
定义挖掘目标
从一个项目的背景里面，找到数据挖掘的目标，定义我们要完成的任务。
数据取样
从数据库中抽取样本子集，然后对于样本子集的要求是：
数据资料完整无缺，各项指标尽量齐全（缺失值处理）
数据准确无误，反映的都是正常状态 （异常值处理）
数据探索
保证样本数据的质量
数据质量分析
主要任务：检查原始数据中是否存在脏数据。
脏数据包括如下：
异常值、缺失值、不一致的值、重复数据或特殊符号等
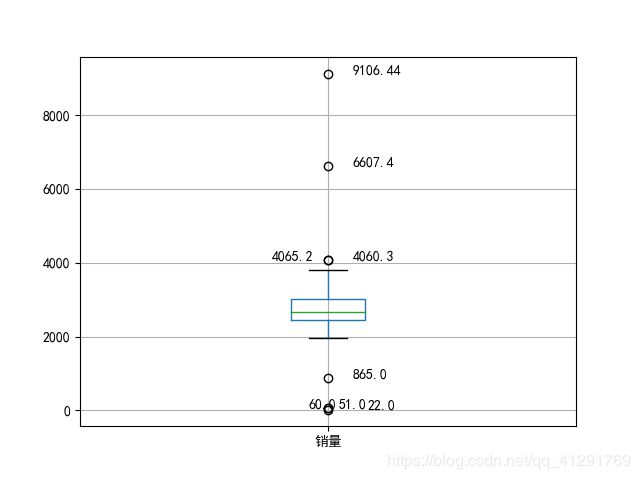
异常值分析
主要任务：处理记录中的录入错误或者不含常理的数据
采用箱线图进行分析，剔除远离图中上界和下界的记录
箱线图使用
#-*- coding: utf-8 -*-
import pandas as pd
#读取数据
catering_sale = '文件目录' #读取文件的目录，注意相对路径
data = pd.read_excel(catering_sale, index_col = u'属性') #读取数据，指定“属性”列为索引列，特征向量
#输出数据并查看
print(data.describe()) #查看数据的具体描述
print(len(data)) #来查看数据的行数
import matplotlib.pyplot as plt #导入图像库
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
plt.figure() #建立图像
p = data.boxplot(return_type='dict') #画箱线图，直接使用DataFrame的方法
x = p['fliers'][0].get_xdata() # 'flies'即为异常值的标签
y = p['fliers'][0].get_ydata()
y.sort() #从小到大排序，该方法直接改变原对象
#用annotate添加注释
#其中有些相近的点，注解会出现重叠，难以看清，需要一些技巧来控制。
#以下参数都是经过调试的，需要具体问题具体调试。
for i in range(len(x)):
if i>0:
plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.05 -0.8/(y[i]-y[i-1]),y[i]))
else:
plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.08,y[i]))
plt.show() #展示箱线图
最后生成的图形如下：
最后可规范数值的取值范围
缺失值分析
主要任务：处理记录缺失或者记录中某个字段信息的缺失
1. 删除含有缺失值的记录
2. 对缺失值值进行插补
拉格朗日插值法
#拉格朗日插值代码
import pandas as pd #导入数据分析库Pandas
from scipy.interpolate import lagrange #导入拉格朗日插值函数
#输入、输出文件
inputfile = '' #销量数据路径
outputfile = '' #输出数据路径
data = pd.read_excel(inputfile) #读入数据
#这里可先通过箱线图确定数据的范围
data[u'销量'][(data[u'销量'] < 400) | (data[u'销量'] > 5000)] = None #过滤异常值，将其变为空值
#自定义列向量插值函数
#s为列向量，n为被插值的位置，k为取前后的数据个数，默认为5
def ployinterp_column(s, n, k=5):
y = s[list(range(n-k, n)) + list(range(n+1, n+1+k))] #取数
y = y[y.notnull()] #剔除空值
return lagrange(y.index, list(y))(n) #插值并返回插值结果
#逐个元素判断是否需要插值
for i in data.columns:
for j in range(len(data)):
if (data[i].isnull())[j]: #如果为空即插值。
data[i][j] = ployinterp_column(data[i], j)
data.to_excel(outputfile) #输出结果，写入文件
- 不处理
一致性分析
主要任务：处理数据的矛盾性、不相容性
数据特征分析
分布分析
揭示数据的分布特征和分布类型
定量数据的分布分析
通过频率分布直方图来描述
定性数据的分布分析
对比分析
绝对数比较
相对数比较
统计量分析
周期性分析
贡献度分析
通过帕累托图直观表示综合影响度 80% 的产品
#-*- coding: utf-8 -*-
#菜品盈利数据 帕累托图
from __future__ import print_function
import pandas as pd
#初始化参数
dish_profit = '文件目录' #餐饮菜品盈利数据
data = pd.read_excel(dish_profit, index_col = u'属性')
data = data[u'盈利'].copy()
import matplotlib.pyplot as plt #导入图像库
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
plt.figure()
data.plot(kind='bar')
plt.ylabel(u'盈利（元）')
p = 1.0*data.cumsum()/data.sum()
p.plot(color = 'r', secondary_y = True, style = '-o',linewidth = 2)
plt.annotate(format(p[6], '.4%'), xy = (6, p[6]), xytext=(6*0.9, p[6]*0.9), arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2")) #添加注释，即85%处的标记。这里包括了指定箭头样式。
plt.ylabel(u'盈利（比例）')
plt.show()
最后生成的图形如下：
相关性分析
分析连续变量之间线性相关的强弱程度
相关系数
越接近1代表相关性越强，接近0代表两个变量之间没有直线相关关系
#-*- coding: utf-8 -*-
#餐饮销量数据相关性分析
import pandas as pd
catering_sale = '文件目录' #餐饮数据，含有其他属性
data = pd.read_excel(catering_sale, index_col = u'属性') #读取数据，指定“日期”列为索引列
print(data.corr()) #相关系数矩阵，即给出了任意两款菜式之间的相关系数
print(data.corr()[u'百合酱蒸凤爪']) #只显示“百合酱蒸凤爪”与其他菜式的相关系数
print(data[u'百合酱蒸凤爪'].corr(data[u'翡翠蒸香茜饺']))#计算“百合酱蒸凤爪”与“翡翠蒸香茜饺”的相关系数
只显示“百合酱蒸凤爪”与其他菜式的相关系数
