- GPT4All:免费使用本地运行无需GPU的基于C++的GPT模型和UI: A free-to-use, locally running, privacy-aware chatbot. No GPU
AI天才研究院
ChatGPT大数据AI人工智能LLM大模型落地实战指南gpt人工智能语言模型自然语言处理编程实践开发语言c++
目录GPT4All:https://github.co:m/nomic-ai/gpt4allGPT4AllChatUIGPT4All聊天用户界面效果测试问题:HowtowriteamultipleThreadcodeInJava?输出:GPT4All如何运作RunningLLMsonCPU在CPU上运行LLMSideloadinganyggMLmodel加载任何ggML模型GPT4ALL:目前已经
- opencv 播放视频
smwhotjay
opencv
看资料cv播放视频是用VideoCapture。结果始终打不开文件,open(0);倒是可以打开摄像头。于是抛弃他的c++类,用c接口来播放。结果ok.//打开CvCapture*capture=cvCreateFileCapture("a.avi");if(!capture){return-1;}//视频信息intcam_width=(int)cvGetCaptureProperty(captu
- cv python_python里面cv是什么意思
weixin_40004659
cvpython
OpenCV(OpenSourceComputerVisionLibrary)开放源代码计算机视觉库,主要算法涉及图像处理、计算机视觉和机器学习相关方法。OpenCV其实就是一堆C和C++语言的源代码文件,这些源代码文件中实现了许多常用的计算机视觉算法。OpenCV由一系列C函数和C++类构成,它有C,C++,Python和java接口,当前SDK(SoftwareDevelopmentKit软件
- 「File」文本格式 之 PugiXML对XML格式解析
何曾参静谧
「Lib」第三方库详解xml
✨博客主页何曾参静谧的博客(✅关注、点赞、⭐收藏、转发)全部专栏(专栏会有变化,以最新发布为准)「Win」Windows程序设计「IDE」集成开发环境「定制」定制开发集合「C/C++」C/C++程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「UG/NX」BlockUI集合「Py」Python程序设计「Math」探秘数学世界「PK」Paras
- 「C/C++」C++经验篇 之 常见的错误处理策略
何曾参静谧
c语言c++开发语言
✨博客主页何曾参静谧的博客(✅关注、点赞、⭐收藏、转发)全部专栏(专栏会有变化,以最新发布为准)「Win」Windows程序设计「IDE」集成开发环境「定制」定制开发集合「C/C++」C/C++程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「UG/NX」BlockUI集合「Py」Python程序设计「Math」探秘数学世界「PK」Paras
- Python标准库 subprocess 模块多进程编程详解
好像要长脑子了1
程序员python开发语言
1.1基本功能subprocess模块,允许生成新的进程执行命令行指令,python程序,以及其它语言编写的应用程序,如java,c++,rust应用等。subprocess可连接多个进程的输入、输出、错误管道,并且获取它们的返回码。asyncio也支持subprocess.许多知名库都在使用此模块创建进程,以及做为跨语言粘合工具。典型如ansible,celery,selenium等。1.2与m
- 「Py」模块篇 之 Python中的subprocess模块详解
何曾参静谧
「Py」Python程序设计python数据库开发语言
✨博客主页何曾参静谧的博客(✅关注、点赞、⭐收藏、转发)全部专栏(专栏会有变化,以最新发布为准)「Win」Windows程序设计「IDE」集成开发环境「定制」定制开发集合「C/C++」C/C++程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「UG/NX」BlockUI集合「Py」Python程序设计「Math」探秘数学世界「PK」Paras
- C++和Python要点对比 【数据结构】
川辉
数据结构算法C++c++python数据结构
C++和Python要点对比前言本人以C++作为工作项目应用主语言,但是也会用到python,而且经常使用python作为力扣算法题的刷题主语言,经常发现容易混淆的函数、语法、和数据结构,于是想做个整理,持续更新。提示:以下是本篇文章正文内容,下面案例可供参考一、数据结构对比1.链表功能实现1.C++C++中的链表是一种线性数据结构,它由一系列节点组成,每个节点包含一个数据元素和一个指向下一个节点
- C++程序设计题解:日期排序
小朋友爱学习
我的算法题解c++程序设计
C++程序设计题解:日期排序题目描述:有一些日期,日期格式为“MM/DD/YYYY”。编程将其按日期大小排列。样例输入:12/31/200510/21/200302/12/200410/22/200311/30/200515/12/1999样例输出:15/12/199910/21/200310/22/200302/12/200411/30/200512/31/2005我的代码:#includeus
- 【Python知行篇】代码的曼妙乐章:探索数据与逻辑的和谐之舞
hope kc
python开发语言
Python学习指南Python是一种功能强大且易于学习的编程语言,广泛应用于数据分析、Web开发、机器学习等多个领域。本文将详细介绍如何学习Python,并涵盖从基础语法到高级应用的多个方面。每个部分都有代码示例,以帮助读者更好地理解并实践所学内容。目录Python基础面向对象编程数据结构与算法Python标准库数据分析和可视化Web开发基础机器学习初步Python优化技巧总结Python基础学
- 咱们一起学C++第十一篇:之深入剖析面向对象项目设计阶段
一杯年华@编程空间
咱们一起学习C++tomcathibernatespringintellij-ideaspringcloudspringbootc++
咱们一起学C++第十一篇:之深入剖析面向对象项目设计阶段在C++学习的道路上,我们始终携手前行,共同探索编程的奥秘。此前,我们对项目分析阶段有了较为深入的了解,今天,我们将继续深入探讨面向对象项目开发中的设计阶段,这是将项目需求转化为实际代码架构的关键环节,对于构建高质量、可维护的软件系统具有举足轻重的作用。一、用例:系统需求的核心体现(一)用例生成需求规范说明用例在项目开发中扮演着至关重要的角色
- string
刃神太酷啦
蓝桥杯C++组
stringC语言中一整个字符串是用字符数组才能表示出来,不能chars="abcd";getline在C语言和C++中的用法不一样,头文件也不一样size_t是一种无符号整数类型(在C和C++均一样)C和C++中的内置类型(比如:long)一定满足所有同类型的关系运算而像string这种就不一定a>b>c和a>b&&b>c区分a>b+1和a>(b+1)是一样的eg:string&是C++中的引用
- 【Linux】Socket编程-TCP构建自己的C++服务器
Zfox_
Linux服务器linuxtcp/ipc++c语言
个人主页:Zfox_系列专栏:Linux目录一:Socket编程TCPTCPsocketAPI详解多线程远程命令执行网络版计算器(应用层自定义协议与序列化)二:共勉一:Socket编程TCPTCPsocketAPI详解下面介绍程序中用到的socketAPI,这些函数都在sys/socket.h中socket#include#include//创建socket文件描述符(TCP/UDP,客户端+服务
- 第05章 06 VTK标量算法中的Contouring算法
捕鲸叉
VTK编程学习算法VTK信息可视化
VTK标量算法中的Contouring算法,并描述MarchCube和MarchSquare等算法思想,分别给出C++示例代码Contouring算法是一种在可视化技术中广泛使用的算法,主要用于从三维标量场中提取等值面(isosurface)。这些等值面表示的是标量场中所有具有相同值的位置的集合。等值面提取是医学成像、气象学、地质学等领域中非常重要的一个处理技术,可以帮助人们更好地理解和分析三维数
- C++——vector和list的比较
Joker Zxc
C++C++vectorlistvector和list的比较
vectorlist底层结构动态顺序表,一段连续空间。带头结点的双向循环链表。随机访问支持随机访问,访问某个元素效率O(1)不支持随机访问,访问某个元素效率O(N)。插入和删除任意位置插入和删除效率低,需要搬移元素,时间复杂度为O(N),插入时有可能需要增容,增容:开辟新空间,拷贝元素,释放旧空间,导致效率更低。任意位置插入和删除效率高,不需要搬移元素,时间复杂度为O(1)。<
- C/C++运行时库和UCRT系统通用运行时库总结及问题实例分享(程序打包时要带上这些运行时库)
dvlinker
C/C++软件开发从入门到实战C/C++实战专栏VisualStudioC/C++运行时库UCRT通用运行时库ProcessExplorer32位64位
目录1、概述2、不同版本的VisualStudio对应的运行时库说明3、在Windbg10.0安装目录中获取UCRT通用运行时库4、微软官网对UCRT通用运行时库的相关说明5、使用VisualStudio2017开发软件初期遇到的UCRT通用运行时库问题6、如何查看软件依赖了哪些C/C++运行时库?7、将软件从32位升级到64位后,要使用64位UCRT通用运行时库8、发布软件时未打包C/C++运行
- C++——多态(上)
qing_040603
C++c++开发语言多态
目录引言多态1.多态的概念1.1编译时多态(静态多态)1.2动态多态(运行时多态)2.多态的定义和实现2.1多态构成的条件2.2虚函数(1)虚函数的定义(2)虚函数重写(3)虚函数重写的例外(4)C++11override和final(5)重载,重写(覆盖),隐藏(重定义)的对比3.纯虚函数和抽象类3.1概念3.2接口继承和实现继承引言在C++——继承中,我们学习了面向对象编程中的一个核心概念——
- android中jni详细,Android中的JNI使用简介
戒酒硫
android中jni详细
一、本文说明本文不对Android工程的各种配置做说明,只是简单介绍下开发过程中如何进行C与Java互相调用以及出现异常情况的处理。二、NDK简介AndroidNDK是一套允许您使用C和C++等语言,以原生代码实现部分应用的工具集。在开发某些类型的应用时,这有助于您重复使用以这些语言编写的代码库。三、JNI简介JNI是JavaNativeInterface的缩写,它提供了若干的API实现了Java
- CMake之问题汇总
General_G
CMake开发pythonlinux开发语言软件构建
目录CouldNOTfindPythonLibsfatalerror:Python.h:Nosuchfileordirectory我们承担ROS,FastDDS等通信中间件,C++,cmake等技术的项目开发和专业指导和培训,有10年+相关工作经验,质量有保证,如有需要请私信联系。CouldNOTfindPythonLibs报错:CMakeErrorat/usr/share/cmake-3.22/
- 1405:质数的和与积(C C++)
小渝同学
#c++
【题目描述】两个质数的和是S,它们的积最大是多少?【输入】一个不大于10000的正整数S,为两个质数的和。【输出】一个不大于10000的正整数S,为两个质数的和。【输入样例】50【输出样例】589【代码】和为定值从中间拆开往两边遍历每种情况11105655474638372928#include#
- 质数的和与积c语言4146,C++算法代码——质数的和与积
普二丁
质数的和与积c语言4146
C++算法代码——字符串p型编码题目来自:http://218.5.5.242:9018/JudgeOnline/problem.phpid=1681题目描述给定一个完全由数字字符('0','1','2',…,'9')构成的字符串str,请写出str的p型编码串。例如:字符串122344111可被描述为"1个1、2个2、1个3、2个4、3个1",因此我们说122344111石子合并问题Garsia
- cpp智能指针
xianwu543
c++mysql网络开发语言数据库
普通指针的不足new和new[]的内存需要用delete和deletel]释放。程序员的主观失误,忘了或漏了释放。程序员也不确定何时释放。普通指针的释放类内的指针,在析构函数中释放。C++内置数据类型,如何释放?new出来的类,本身如何释放?C++11新增三个智能指针类型unique_ptrshared_ptrweak_ptr一、智能指针unique_ptrunique_ptr独享它指向的对象,也
- 【华为OD】2024年华为OD机试C卷、D卷真题集:最新的真题集题库 C/C++/Java/python/JavaScript
五木大大
华为odc语言c++pythonjavajavascript码蚁软件培训
【华为OD】2024年C卷真题集:最新的真题集题库C/C++/Java/python/JavaScript【华为OD】2024年C卷真题集:最新的真题集题库C/C++/Java/python/JavaScript-CSDN博客2024年华为OD的D卷是2024-4-15号切换过来的,不过就目前来看,D卷题目和C卷的重合率很高,只要把C卷练好了,D卷是可以轻松过的,加油呀,同学们。目前据考了D卷的同
- 编程语言中的常见Bug及解决方案
编程语言bug
在编程过程中,不同语言有其独特的特性和挑战,这也导致了各种常见Bug的出现。本文将总结几种主流编程语言中的常见Bug,包括JavaScript、Python、C/C++、Java和Go,并提供相应的解决方案和案例。一、JavaScript中小数相加精度不准确的Bug在JavaScript中,进行小数相加时,由于浮点数的精度问题,可能会导致结果不准确。例如:letadd1=0.1+0.2;conso
- 2024年华为OD机试E卷- Boss的收入-(Java&c++&Python)
ai因思坦
华为OD机试2024真题题库华为odc++开发语言矩阵算法pythonjava
最新华为OD机试考点合集:华为OD机试2024年真题题库(E卷+D卷+C卷)_华为od机试题库-CSDN博客每一题都含有详细的解题思路和代码注释,精编c++、JAVA、Python三种语言解法。帮助每一位考生轻松、高效刷题。订阅后永久可看,发现新题及时跟新。题目描述:一个XX产品行销总公司,只有一个boss,其有若千一级分销,一级分销又有若干二级分销,每个分错只有唯一的上级分销。规定,每个月
- C++ 函数调用时的参数传递方法
相忘于江湖-mfc
c++开发语言寄存器gdb调试
C++语言的函数调用在编译后的ELF文件中,不论是C++函数还是C函数,甚至是汇编语言函数,它们之间没有任何区别。但是,C++函数在编译时会经过函数名变换(mangle)。例如,对于如下C++函数func:classfoo{public:voidfunc(intx,inty);};函数foo::func在ELF文件中被变换成下面的符号(mangle之后的符号名依赖于具体的实现):#nmfoo|gr
- x86_64下 C C++ 函数调用时的参数传递方法
相忘于江湖-mfc
c语言c++linuxgdb调试
CC++函数调用时的参数传递方法根据架构、编译器的不同而有所不同,本文讲的是x86_64架构上使用CC++语言GNU编译器的情况。先说结论:在x86_64上,整型和指针类型的参数会从左至右依次保存到rdi、rsi、rdx、rcx、r8、r9这6个寄存器,浮点参数会保存到xmm0、xmm1.....等寄存器中。当参数个数超过了这些寄存器的限制,多余的参数就会保存到栈上。以下用一个例子验证,编写如下程
- 《python基于时间序列分析的降雨量预测系统》毕业设计项目
君君学姐
python课程设计开发语言
大家好我是君君学姐,混迹在java圈的辛苦码农。今天要和大家聊的是一款《python基于时间序列分析的降雨量预测系统》毕业设计项目。项目源码以及部署相关请联系君君学姐,文末附上联系信息。作者:君君学姐个人简介:精通Java、Python、C#、C、C++等编程语言,同时对微信小程序、Php和Android等技术也能熟练掌握,可为大家提供全面的技术支持与交流。我拥有丰富的成品Java、Python、
- C++对文件的生成打开输入读取和关闭
bilin_jam
C++c++
文章目录文章目录前言一、C++生成(或打开)文件二、C++写入文件三、读取文件四、关闭文件五、读取&写入实例六、文件位置指针前言如果我们要制作一个文本工具,那么学会C++中对文件的控制是肥肠中药的,所以今天直接来一期保姆级教学。接下来,我们直接开凿。但在开凿之前,我们需要用到C++中另一个标准库fstream,它定义了三个新的数据类型:数据类型&描述数据类型描述ofstream该数据类型表示输出文
- Linux问题调试(2)--内存问题与asan工具
厛,記憶の鍾
Linux问题调试java前端linux
一、问题Linux项目开发过程中,时常会出现内存泄漏的问题,而这类问题却很难定位和排查,本文介绍一种定位内存泄漏问题的常用工具asan工具。二、asan工具原理asan全称AddressSanitizer,是一种面向c/c++语言的内存错误问题检查工具,目的是帮助开发者检测和调试内存相关的问题。gcc工具在4.8版本后加入了asan工具,但完整的asan功能需要在4.9.2以上才的以提供。asan
- 统一思想认识
永夜-极光
思想
1.统一思想认识的基础,才能有的放矢
原因:
总有一种描述事物的方式最贴近本质,最容易让人理解.
如何让教育更轻松,在于找到最适合学生的方式.
难点在于,如何模拟对方的思维基础选择合适的方式. &
- Joda Time使用笔记
bylijinnan
javajoda time
Joda Time的介绍可以参考这篇文章:
http://www.ibm.com/developerworks/cn/java/j-jodatime.html
工作中也常常用到Joda Time,为了避免每次使用都查API,记录一下常用的用法:
/**
* DateTime变化(增减)
*/
@Tes
- FileUtils API
eksliang
FileUtilsFileUtils API
转载请出自出处:http://eksliang.iteye.com/blog/2217374 一、概述
这是一个Java操作文件的常用库,是Apache对java的IO包的封装,这里面有两个非常核心的类FilenameUtils跟FileUtils,其中FilenameUtils是对文件名操作的封装;FileUtils是文件封装,开发中对文件的操作,几乎都可以在这个框架里面找到。 非常的好用。
- 各种新兴技术
不懂事的小屁孩
技术
1:gradle Gradle 是以 Groovy 语言为基础,面向Java应用为主。基于DSL(领域特定语言)语法的自动化构建工具。
现在构建系统常用到maven工具,现在有更容易上手的gradle,
搭建java环境:
http://www.ibm.com/developerworks/cn/opensource/os-cn-gradle/
搭建android环境:
http://m
- tomcat6的https双向认证
酷的飞上天空
tomcat6
1.生成服务器端证书
keytool -genkey -keyalg RSA -dname "cn=localhost,ou=sango,o=none,l=china,st=beijing,c=cn" -alias server -keypass password -keystore server.jks -storepass password -validity 36
- 托管虚拟桌面市场势不可挡
蓝儿唯美
用户还需要冗余的数据中心,dinCloud的高级副总裁兼首席营销官Ali Din指出。该公司转售一个MSP可以让用户登录并管理和提供服务的用于DaaS的云自动化控制台,提供服务或者MSP也可以自己来控制。
在某些情况下,MSP会在dinCloud的云服务上进行服务分层,如监控和补丁管理。
MSP的利润空间将根据其参与的程度而有所不同,Din说。
“我们有一些合作伙伴负责将我们推荐给客户作为个
- spring学习——xml文件的配置
a-john
spring
在Spring的学习中,对于其xml文件的配置是必不可少的。在Spring的多种装配Bean的方式中,采用XML配置也是最常见的。以下是一个简单的XML配置文件:
<?xml version="1.0" encoding="UTF-8"?>
<beans xmlns="http://www.springframework.or
- HDU 4342 History repeat itself 模拟
aijuans
模拟
来源:http://acm.hdu.edu.cn/showproblem.php?pid=4342
题意:首先让求第几个非平方数,然后求从1到该数之间的每个sqrt(i)的下取整的和。
思路:一个简单的模拟题目,但是由于数据范围大,需要用__int64。我们可以首先把平方数筛选出来,假如让求第n个非平方数的话,看n前面有多少个平方数,假设有x个,则第n个非平方数就是n+x。注意两种特殊情况,即
- java中最常用jar包的用途
asia007
java
java中最常用jar包的用途
jar包用途axis.jarSOAP引擎包commons-discovery-0.2.jar用来发现、查找和实现可插入式接口,提供一些一般类实例化、单件的生命周期管理的常用方法.jaxrpc.jarAxis运行所需要的组件包saaj.jar创建到端点的点到点连接的方法、创建并处理SOAP消息和附件的方法,以及接收和处理SOAP错误的方法. w
- ajax获取Struts框架中的json编码异常和Struts中的主控制器异常的解决办法
百合不是茶
jsjson编码返回异常
一:ajax获取自定义Struts框架中的json编码 出现以下 问题:
1,强制flush输出 json编码打印在首页
2, 不强制flush js会解析json 打印出来的是错误的jsp页面 却没有跳转到错误页面
3, ajax中的dataType的json 改为text 会
- JUnit使用的设计模式
bijian1013
java设计模式JUnit
JUnit源代码涉及使用了大量设计模式
1、模板方法模式(Template Method)
定义一个操作中的算法骨架,而将一些步骤延伸到子类中去,使得子类可以不改变一个算法的结构,即可重新定义该算法的某些特定步骤。这里需要复用的是算法的结构,也就是步骤,而步骤的实现可以在子类中完成。
- Linux常用命令(摘录)
sunjing
crondchkconfig
chkconfig --list 查看linux所有服务
chkconfig --add servicename 添加linux服务
netstat -apn | grep 8080 查看端口占用
env 查看所有环境变量
echo $JAVA_HOME 查看JAVA_HOME环境变量
安装编译器
yum install -y gcc
- 【Hadoop一】Hadoop伪集群环境搭建
bit1129
hadoop
结合网上多份文档,不断反复的修正hadoop启动和运行过程中出现的问题,终于把Hadoop2.5.2伪分布式安装起来,跑通了wordcount例子。Hadoop的安装复杂性的体现之一是,Hadoop的安装文档非常多,但是能一个文档走下来的少之又少,尤其是Hadoop不同版本的配置差异非常的大。Hadoop2.5.2于前两天发布,但是它的配置跟2.5.0,2.5.1没有分别。 &nb
- Anychart图表系列五之事件监听
白糖_
chart
创建图表事件监听非常简单:首先是通过addEventListener('监听类型',js监听方法)添加事件监听,然后在js监听方法中定义具体监听逻辑。
以钻取操作为例,当用户点击图表某一个point的时候弹出point的name和value,代码如下:
<script>
//创建AnyChart
var chart = new AnyChart();
//添加钻取操作&quo
- Web前端相关段子
braveCS
web前端
Web标准:结构、样式和行为分离
使用语义化标签
0)标签的语义:使用有良好语义的标签,能够很好地实现自我解释,方便搜索引擎理解网页结构,抓取重要内容。去样式后也会根据浏览器的默认样式很好的组织网页内容,具有很好的可读性,从而实现对特殊终端的兼容。
1)div和span是没有语义的:只是分别用作块级元素和行内元素的区域分隔符。当页面内标签无法满足设计需求时,才会适当添加div
- 编程之美-24点游戏
bylijinnan
编程之美
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashSet;
import java.util.List;
import java.util.Random;
import java.util.Set;
public class PointGame {
/**编程之美
- 主页面子页面传值总结
chengxuyuancsdn
总结
1、showModalDialog
returnValue是javascript中html的window对象的属性,目的是返回窗口值,当用window.showModalDialog函数打开一个IE的模式窗口时,用于返回窗口的值
主界面
var sonValue=window.showModalDialog("son.jsp");
子界面
window.retu
- [网络与经济]互联网+的含义
comsci
互联网+
互联网+后面是一个人的名字 = 网络控制系统
互联网+你的名字 = 网络个人数据库
每日提示:如果人觉得不舒服,千万不要外出到处走动,就呆在床上,玩玩手游,更不能够去开车,现在交通状况不
- oracle 创建视图 with check option
daizj
视图vieworalce
我们来看下面的例子:
create or replace view testview
as
select empno,ename from emp where ename like ‘M%’
with check option;
这里我们创建了一个视图,并使用了with check option来限制了视图。 然后我们来看一下视图包含的结果:
select * from testv
- ToastPlugin插件在cordova3.3下使用
dibov
Cordova
自己开发的Todos应用,想实现“
再按一次返回键退出程序 ”的功能,采用网上的ToastPlugins插件,发现代码或文章基本都是老版本,运行问题比较多。折腾了好久才弄好。下面吧基于cordova3.3下的ToastPlugins相关代码共享。
ToastPlugin.java
package&nbs
- C语言22个系统函数
dcj3sjt126com
cfunction
C语言系统函数一、数学函数下列函数存放在math.h头文件中Double floor(double num) 求出不大于num的最大数。Double fmod(x, y) 求整数x/y的余数。Double frexp(num, exp); double num; int *exp; 将num分为数字部分(尾数)x和 以2位的指数部分n,即num=x*2n,指数n存放在exp指向的变量中,返回x。D
- 开发一个类的流程
dcj3sjt126com
开发
本人近日根据自己的开发经验总结了一个类的开发流程。这个流程适用于单独开发的构件,并不适用于对一个项目中的系统对象开发。开发出的类可以存入私人类库,供以后复用。
以下是开发流程:
1. 明确类的功能,抽象出类的大概结构
2. 初步设想类的接口
3. 类名设计(驼峰式命名)
4. 属性设置(权限设置)
判断某些变量是否有必要作为成员属
- java 并发
shuizhaosi888
java 并发
能够写出高伸缩性的并发是一门艺术
在JAVA SE5中新增了3个包
java.util.concurrent
java.util.concurrent.atomic
java.util.concurrent.locks
在java的内存模型中,类的实例字段、静态字段和构成数组的对象元素都会被多个线程所共享,局部变量与方法参数都是线程私有的,不会被共享。
- Spring Security(11)——匿名认证
234390216
Spring SecurityROLE_ANNOYMOUS匿名
匿名认证
目录
1.1 配置
1.2 AuthenticationTrustResolver
对于匿名访问的用户,Spring Security支持为其建立一个匿名的AnonymousAuthenticat
- NODEJS项目实践0.2[ express,ajax通信...]
逐行分析JS源代码
Ajaxnodejsexpress
一、前言
通过上节学习,我们已经 ubuntu系统搭建了一个可以访问的nodejs系统,并做了nginx转发。本节原要做web端服务 及 mongodb的存取,但写着写着,web端就
- 在Struts2 的Action中怎样获取表单提交上来的多个checkbox的值
lhbthanks
javahtmlstrutscheckbox
第一种方法:获取结果String类型
在 Action 中获得的是一个 String 型数据,每一个被选中的 checkbox 的 value 被拼接在一起,每个值之间以逗号隔开(,)。
所以在 Action 中定义一个跟 checkbox 的 name 同名的属性来接收这些被选中的 checkbox 的 value 即可。
以下是实现的代码:
前台 HTML 代码:
- 003.Kafka基本概念
nweiren
hadoopkafka
Kafka基本概念:Topic、Partition、Message、Producer、Broker、Consumer。 Topic: 消息源(Message)的分类。 Partition: Topic物理上的分组,一
- Linux环境下安装JDK
roadrunners
jdklinux
1、准备工作
创建JDK的安装目录:
mkdir -p /usr/java/
下载JDK,找到适合自己系统的JDK版本进行下载:
http://www.oracle.com/technetwork/java/javase/downloads/index.html
把JDK安装包下载到/usr/java/目录,然后进行解压:
tar -zxvf jre-7
- Linux忘记root密码的解决思路
tomcat_oracle
linux
1:使用同版本的linux启动系统,chroot到忘记密码的根分区passwd改密码 2:grub启动菜单中加入init=/bin/bash进入系统,不过这时挂载的是只读分区。根据系统的分区情况进一步判断. 3: grub启动菜单中加入 single以单用户进入系统. 4:用以上方法mount到根分区把/etc/passwd中的root密码去除 例如: ro
- 跨浏览器 HTML5 postMessage 方法以及 message 事件模拟实现
xueyou
jsonpjquery框架UIhtml5
postMessage 是 HTML5 新方法,它可以实现跨域窗口之间通讯。到目前为止,只有 IE8+, Firefox 3, Opera 9, Chrome 3和 Safari 4 支持,而本篇文章主要讲述 postMessage 方法与 message 事件跨浏览器实现。postMessage 方法 JSONP 技术不一样,前者是前端擅长跨域文档数据即时通讯,后者擅长针对跨域服务端数据通讯,p
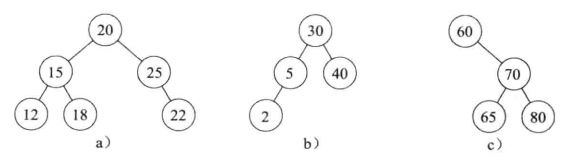
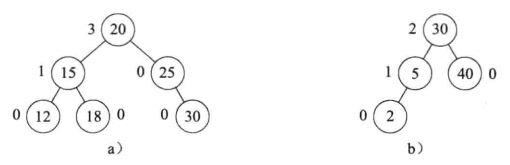
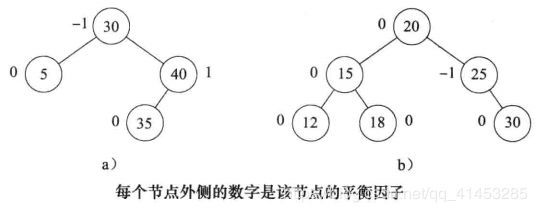
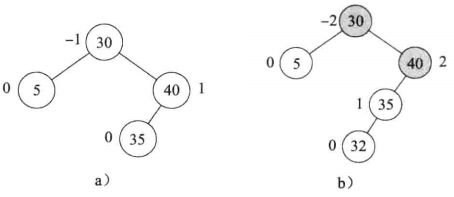
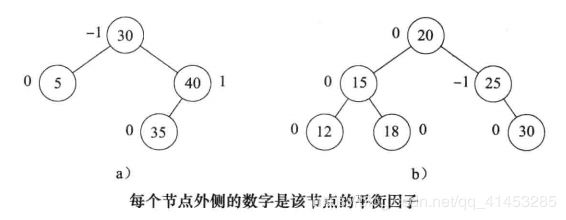
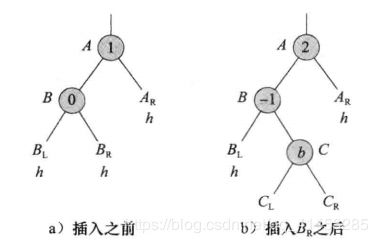
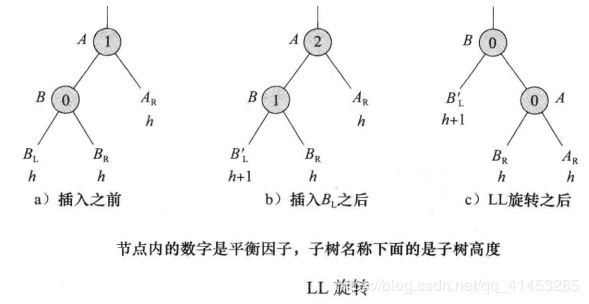
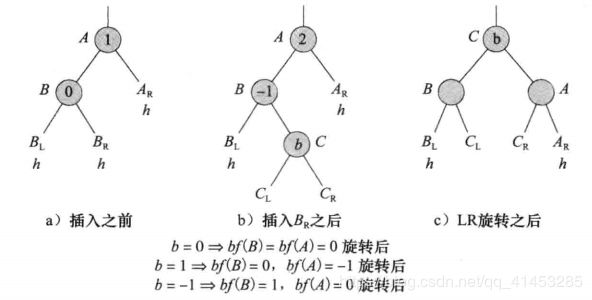
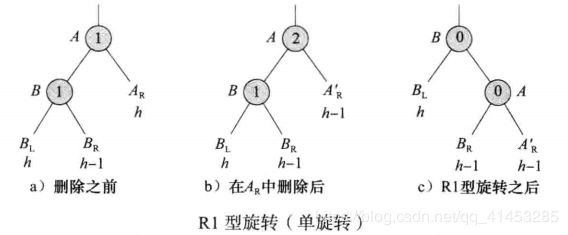
是h-1,右子树高度
是h-2(如下图a所示)
中做插入,得到高度为h-1的新子树
(如下图b所示)
的高度必须增加到h-1
仍然是B的左子树,A变成B的右子树的根,
变成A的左子树,A的右子树不变
的所有节点的平衡因子都要改变。其他节点的平衡因子与旋转前的一致
和
,但是也可能为空)
):