红黑树：整理学习

红黑树

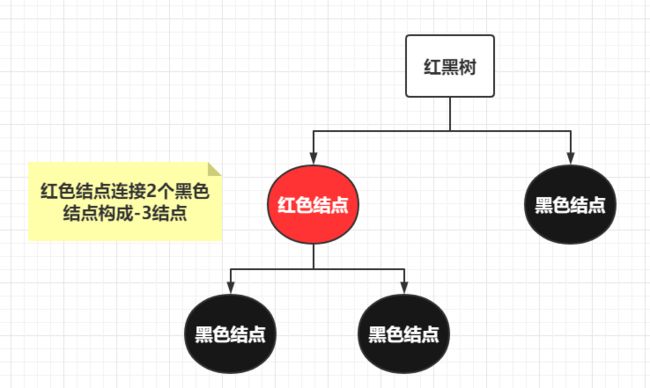
红黑树定义

• 红色结点均为左节点 – 红色结点与黑色结点合并会得到一个-3结点
• 没有任何一个结点同时和两个红色结点相连
• 任一空连接到根节点的长度和黑色结点的数目相同

结点定义

// 红色结点记为true，黑色记为false
private static final boolean RED = true;
private static final boolean BLACK = false;

// BST helper node data type
private class Node {
    private Key key;           // key
    private Value val;         // associated data
    private Node left, right;  // links to left and right subtrees
    private boolean color;     // color of parent link
    private int size;          // subtree count

    public Node(Key key, Value val, boolean color, int size) {
        this.key = key;
        this.val = val;
        this.color = color;
        this.size = size;
    }
}

红黑树的左旋与右旋,以及颜色变换：

private Node rotateLeft(Node h) {
    Node x = h.right;
    x.left = h;
    x.color = h.color;
    // 与父节点链接变为红色
    h.color = RED;
    x.size = size(h.left) + size(h.right) + 1;
    return x;
}

private Node rotateRight(Node h) {
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    x.color = h.color;
    h.color = RED;
    x.size = size(h.left) + size(h.right) + 1;
    return x;
}

private void flipColors(Node h) {
    if (h == null) return;
    h.color = RED;
    h.left.color = BLACK;
    h.right.color = BLACK;
}

红黑树插入算法的关键：

• 要在一个3-结点下面插入一个新节点，需要将结点临时转换成一个4-结点
• 将其分解并将红链接由中间键传递给父节点
• 直到遇见一个2-结点或根节点

private void put(Key key, Value val) {
    root = put(root, key, val);
    root.color = BLACK;
}

private Node put(Node h, Key key, Value val) {
    // 如果没有则插入一个红色结点，这样方便以后调整
    if (h == null)
        return new Node(key, val, RED, 1);

    int cmp = key.compareTo(h.key);

    // 满足BST的性质，如果小于，则从左边插入
    if (cmp < 0) h.left = put(h.left, key, val);
    else if (cmp > 0) h.right = put(h.right, key, val);
    // 已经在树中，更新值
    else h.val = val;

    /**
     * 红黑树调整的目的是为了在插入结点的同时动态调整树的高度
     * 避免树的高度过高，提升索引的效率
     */

    // 重点！！ 红黑树的调整过程
    // 左黑右红
    if (!isRed(h.left) && isRed(h.right))
        h = rotateLeft(h); // 左旋
    // 左红右黑
    if (isRed(h.left) && !isRed(h.right))
        h = rotateRight(h); // 右旋
    // 全红
    if (isRed(h.left) && isRed(h.right))
        flipColors(h); // 颜色反转 -- 结点成为2-结点，父节点成为3-结点

    // 调整树的规模
    h.size = size(h.left) + size(h.right) + 1;
    return h;
}

删除算法之后补充