java代码之冒泡排序及其优化

1、交换排序的基本思想
两两比较待排序记录的关键字，如果发现两个记录的次序相反则进行交换，知道所有记录都没有反序为止。
2、常见的交换排序
冒泡排序、快速排序
3、冒泡排序的基本思想
冒泡排序属于比较简单的排序，以非递减为例，依次遍历数组，发现a[i]>a[i+1}的情况，swap(a[i],a[i+1])，直到没有逆序的数据，完成排序，可以用两个for循环嵌套实现，外层控制遍历次数，内层用来实现交换，也可以用一个boolean类型变量来控制是否有交换发生，如果没有交换，表明已经正序，可以直接输出。
4、冒泡排序案例
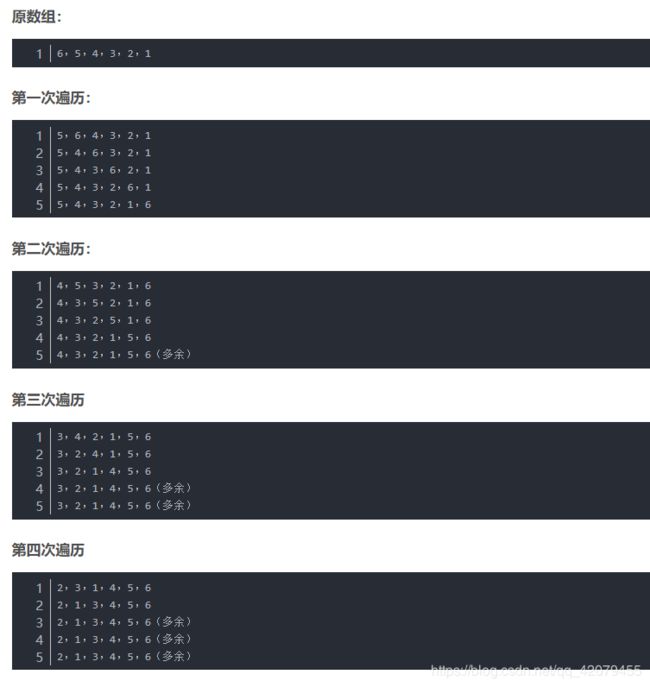
我们以升序排列为例，算法的思想是，遍历整个数组，依次对数组中的每两个数进行比较大小，通过两个数字的交换，达到将最大的元素移动到数组的最后的目的，然后再次进行遍历，将第二大的数字移动到数组的倒数第二个位置…这样一次次遍历下来，数组将变为有序。举例如下，假设有一串数，以降序排列，现在我们要将它变为升序，这对于冒泡排序是最坏的一种情况
数组的变化如下：

5、冒泡排序核心代码及其优化

public static int[] bubbleSort1(int[] a) {
		int i, j;
		for (i = 0; i < a.length; i++) {// 表示n次排序过程。
			for (j = 1; j < a.length - i; j++) {
				if (a[j - 1] > a[j]) {// 前面的数字大于后面的数字就交换
					// 交换a[j-1]和a[j]
					int temp;
					temp = a[j - 1];
					a[j - 1] = a[j];
					a[j] = temp;
				}
			}
		}
		return a;
	}

下面开始考虑优化，如果对于一个本身有序的序列，或则序列后面一大部分都是有序的序列，上面的算法就会浪费很多的时间开销，这里设置一个标志flag，如果这一趟发生了交换，则为true，否则为false。明显如果有一趟没有发生交换，说明排序已经完成。

public static int[] bubbleSort2(int[] a) {
		int j, k = a.length;
		boolean flag = true;// 发生了交换就为true, 没发生就为false，第一次判断时必须标志位true。
		while (flag) {
			flag = false;// 每次开始排序前，都设置flag为未排序过
			for (j = 1; j < k; j++) {
				if (a[j - 1] > a[j]) {// 前面的数字大于后面的数字就交换
					// 交换a[j-1]和a[j]
					int temp;
					temp = a[j - 1];
					a[j - 1] = a[j];
					a[j] = temp;

					// 表示交换过数据;
					flag = true;
				}
			}
			k--;// 减小一次排序的尾边界
		} // end while
		return a;
	}

再进一步做优化。比如，现在有一个包含1000个数的数组，仅前面100个无序，后面900个都已排好序且都大于前面100个数字，那么在第一趟遍历后，最后发生交换的位置必定小于100，且这个位置之后的数据必定已经有序了，也就是这个位置以后的数据不需要再排序了，于是记录下这位置，第二次只要从数组头部遍历到这个位置就可以了。如果是对于上面的冒泡排序算法2来说，虽然也只排序100次，但是前面的100次排序每次都要对后面的900个数据进行比较，而对于现在的排序算法3，只需要有一次比较后面的900个数据，之后就会设置尾边界，保证后面的900个数据不再被排序。

public static int[] bubbleSort3(int[] a) {
		int j, k;
		int flag = a.length;// flag来记录最后交换的位置，也就是排序的尾边界

		while (flag > 0) {// 排序未结束标志
			k = flag; // k 来记录遍历的尾边界
			flag = 0;

			for (j = 1; j < k; j++) {
				if (a[j - 1] > a[j]) {// 前面的数字大于后面的数字就交换
					// 交换a[j-1]和a[j]
					int temp;
					temp = a[j - 1];
					a[j - 1] = a[j];
					a[j] = temp;

					// 表示交换过数据;
					flag = j;// 记录最新的尾边界.
				}
			}
		}
		return a;
	}

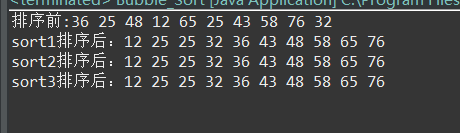
主函数代码及其运行结果：

public static void main(String[] args) {
		// 显示排序前的序列
		int[] a = { 36, 25, 48, 12, 65, 25, 43, 58, 76, 32 };
		System.out.print("排序前:");
		for (int data : a) {
			System.out.print(data + " ");
		}
		System.out.println();
		// 显示排序后的序列
		System.out.print("sort1排序后：");
		for (int data : Bubble_Sort.bubbleSort1(a)) {
			System.out.print(data + " ");
		}
		System.out.println();
		// 显示排序后的序列
		System.out.print("sort2排序后：");
		for (int data : Bubble_Sort.bubbleSort1(a)) {
			System.out.print(data + " ");
		}
		System.out.println();
		// 显示排序后的序列
		System.out.print("sort3排序后：");
		for (int data : Bubble_Sort.bubbleSort1(a)) {
			System.out.print(data + " ");
		}
	}

6、冒泡排序算法性能分析
时间复杂度
冒泡排序算法时间复杂度在最好的情况下为O(n),最坏的情况下为O(n^2)
空间复杂度
空间复杂度为O(1)
算法稳定性
算法稳定性为：稳定