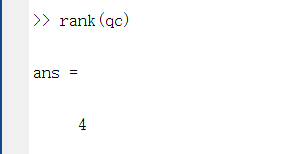【基于Simulink+UG NX MCD 一级倒立摆控制系统仿真】建模和分析(一)
前言
倒立摆是比较典型的系统,可以看出火箭发射的简化模型,国内外学者常常通过在倒立摆上开发和测试控制算法。
对倒立摆的控制分为两大任务:
- 起摆
- 稳摆
所以本文想通过此项目对自动控制原理进行一个复习与学习的过程,具体目标设想建立单摆模型,通过simulink进行仿真,开发相关算法,同时,利用UG NX MCD建立单摆机电模型,可以进行更为直观的仿真,但利用MCD进行控制算法的开发还未看到有相关研究。
建立数学模型
Step 0: 问题描述
如图所示,倒立摆一端通过关节连接水平移动的小车上,小车由电机轮驱动并且只能在 x x x方向移动,电机水平驱动力为 F F F,小车质量为 M M M,摆杆质量为 m m m,摆杆长度为 2 l 2l 2l,要研究怎样的外力 F F F输入才能控制摆杆保持垂直。

Step 1: 采用牛顿力学定律进行建模
设小车移动记录为 x x x,摆杆偏离垂直方向角度为 θ θ θ,小车对摆杆垂直方向和水平方向的反作用力分别为 P P P和 N N N

对于小车,根据牛顿定律可以写出水平方向的力平衡方程:
M x ¨ = F − B p x ˙ − N M\ddot{x}=F-B_p\dot{x}-N Mx¨=F−Bpx˙−N
对于摆杆,根据牛顿定律可以写出水平方向和垂直方向的力平衡方程:
N = m d 2 x 1 d t 2 = d 2 d t 2 ( x + l s i n θ ) = m ( x ˙ + θ ˙ l c o s θ ) ′ N=m\frac{d^{2} x_{1}}{dt^{2}} =\frac{d^{2} }{dt^{2}}(x+lsinθ) =m(\dot{x}+\dot{θ}lcosθ)' N=mdt2d2x1=dt2d2(x+lsinθ)=m(x˙+θ˙lcosθ)′ = m x ¨ + m l θ ¨ c o s θ − m l θ 2 ˙ s i n θ =m\ddot{x}+ml\ddot{θ}cosθ-ml\dot{θ^2}sinθ =mx¨+mlθ¨cosθ−mlθ2˙sinθ
P − m g = d 2 y 1 d t 2 = d 2 d t 2 ( l c o s θ ) = m ( − θ ˙ l s i n θ ) ′ P-mg=\frac{d^{2}y_1}{dt^{2}}=\frac{d^{2}}{dt^{2}}(lcosθ)=m(-\dot{θ}lsinθ)' P−mg=dt2d2y1=dt2d2(lcosθ)=m(−θ˙lsinθ)′ = − m l θ ¨ s i n θ − m l θ ˙ c o s θ =-ml\ddot{θ}sinθ-ml\dot{θ}cosθ =−mlθ¨sinθ−mlθ˙cosθ
其中: x 1 x_1 x1为摆杆质心水平移动距离, y 1 y_1 y1为垂直移动距离。
摆杆对质心转动惯量为 I I I,则摆杆质心的力矩方程为:
I θ ¨ = P l s i n θ − N l c o s θ I\ddot{θ}=Plsinθ-Nlcosθ Iθ¨=Plsinθ−Nlcosθ
联立上述四式,消去变量 H H H和 N N N,得:
I θ ¨ = m g l s i n θ − m l 2 θ ¨ − m l x ¨ c o s θ I\ddot{θ}=mglsinθ-ml^{2}\ddot{θ}-ml\ddot{x}cosθ Iθ¨=mglsinθ−ml2θ¨−mlx¨cosθ
M x ¨ = F − B p x ˙ − m ( x ¨ + l θ ¨ c o s θ − l θ 2 ˙ s i n θ ) M\ddot{x}=F-B_p\dot{x}-m(\ddot{x}+l\ddot{θ}cosθ-l\dot{θ^2}sinθ) Mx¨=F−Bpx˙−m(x¨+lθ¨cosθ−lθ2˙sinθ)
为使得倒单摆保持垂直状态,假定 θ θ θ很小,则有 c o s θ ≈ 1 , s i n θ = 0 , θ ˙ 2 = 0 cosθ≈1,sinθ=0,\dot{θ}^2=0 cosθ≈1,sinθ=0,θ˙2=0,因此上面两式可化简为:
( I − m l 2 ) θ ¨ + m l x ¨ = m g l θ (I-ml^2)\ddot{θ}+ml\ddot{x}=mglθ (I−ml2)θ¨+mlx¨=mglθ ( M + m ) x ¨ + B p x ˙ + m l θ ¨ = F (M+m)\ddot{x}+B_p\dot{x}+ml\ddot{θ}=F (M+m)x¨+Bpx˙+mlθ¨=F
设摆杆质量分布均匀,则 I = m ( 2 l ) 2 12 I=\frac{m(2l)^2}{12} I=12m(2l)2,同时忽略摩擦, B p = 0 B_p=0 Bp=0,因此上面两式可化简为数学模型方程:
4 3 m l 2 θ ¨ + m l x ¨ = m g l θ \frac{4}{3}ml^2\ddot{θ}+ml\ddot{x}=mglθ 34ml2θ¨+mlx¨=mglθ ( M + m ) x ¨ + m l θ ¨ = F (M+m)\ddot{x}+ml\ddot{θ}=F (M+m)x¨+mlθ¨=F
Step 2: 传递函数
对上面两式做拉式变换,并设初始状态为 x ( 0 ) = 0 , θ ( 0 ) = 0 x(0)=0,θ(0)=0 x(0)=0,θ(0)=0,得:
4 3 m l 2 Θ ( s ) s 2 + m l X ( s ) s 2 = m g l Θ ( s ) \frac{4}{3}ml^2Θ(s)s^2+mlX(s)s^2=mglΘ(s) 34ml2Θ(s)s2+mlX(s)s2=mglΘ(s) ( M + m ) X ( s ) s 2 + m l Θ ( s ) s 2 = F ( s ) (M+m)X(s)s^2+mlΘ(s)s^2=F(s) (M+m)X(s)s2+mlΘ(s)s2=F(s)
设定系统输出用 θ θ θ角表示,则联立上面两式,意消去 X ( s ) X(s) X(s),得
X ( s ) = ( g s 2 − 4 l 3 ) Θ ( s ) X(s)=(\frac{g}{s^2}-\frac{4l}{3})Θ(s) X(s)=(s2g−34l)Θ(s) ( M + m ) ( g s 2 − 4 l 3 ) Θ ( s ) s 2 + m l Θ ( s ) s 2 = F ( s ) (M+m)(\frac{g}{s^2}-\frac{4l}{3})Θ(s)s^2+mlΘ(s)s^2=F(s) (M+m)(s2g−34l)Θ(s)s2+mlΘ(s)s2=F(s)
整理得传递函数:
Θ ( s ) F ( s ) = 1 [ ( M + m ) ( g s 2 − 4 l 3 ) + m l ] s 2 \frac{Θ(s)}{F(s)}=\frac{1}{[(M+m)(\frac{g}{s^2}-\frac{4l}{3})+ml]s^2} F(s)Θ(s)=[(M+m)(s2g−34l)+ml]s21
= − 3 ( 4 M + m ) l s 2 − 3 ( M + m ) g ( 4 M + m ) l =\frac{-\frac{3}{(4M+m)l}}{s^2-\frac{3(M+m)g}{(4M+m) l}} =s2−(4M+m)l3(M+m)g−(4M+m)l3
使用matlab构造传递函数
取 M = 0.1 k g , m = 0.5 k g , l = 0.5 m , g = 9.81 M=0.1kg,m=0.5kg,l=0.5m,g=9.81 M=0.1kg,m=0.5kg,l=0.5m,g=9.81,使用matlab计算,则有
%% 清理
clear;close;clc;
%% 模型数据
M=1;%kg,小车质量
m=0.5;%kg,摆杆质量
l=0.5;%m,摆杆长
g=9.81;%% 传递函数
num = [-3/((4*M+m)*l)]; %分子多项式系数行向量
den = [1 0 -(3*(M+m)*g)/((4*M+m)*l)]; %分母多项式系数行向量
GS = tf(num,den); %建立传递函数模型
关于状态空间模型
状态空间方法是现代控制中的内容,适合于多输入多输出系统,时变系统等,并且可以知道内部变量的变化,而传递函数模型是经典控制中的内容,只适用于单输入单输出的线性定常系统。
Step 3: 状态空间模型
选取系统状态变量:
x 1 = θ , x 2 = θ ˙ , x 3 = x , x 4 = x ˙ x_1=θ,x_2=\dot{θ},x_3=x,x_4=\dot{x} x1=θ,x2=θ˙,x3=x,x4=x˙
根据上述数学模型方程,于是得到
x 1 ˙ = x 2 \dot{x_1}=x_2 x1˙=x2
x 2 ˙ = 3 ( M + m ) g ( 4 M + m ) l x 1 − 3 ( 4 M + m ) l F \dot{x_2}=\frac{3(M+m)g}{(4M+m)l}x_1-\frac{3}{(4M+m)l}F x2˙=(4M+m)l3(M+m)gx1−(4M+m)l3F
x 3 ˙ = x 4 \dot{x_3}=x_4 x3˙=x4
x 4 ˙ = − 3 m g 4 M + m x 1 + 4 4 M + m F \dot{x_4}=-\frac{3mg}{4M+m}x_1+\frac{4}{4M+m}F x4˙=−4M+m3mgx1+4M+m4F
则状态方程为:
[ x 1 ˙ x 2 ˙ x 3 ˙ x 4 ˙ ] = [ 0 1 0 0 3 ( M + m ) g ( 4 M + m ) l 0 0 0 0 0 0 1 − 3 m g 4 M + m 0 0 0 ] [ x 1 x 2 x 3 x 4 ] + [ 0 − 3 ( 4 M + m ) l 0 4 4 M + m ] F \begin{bmatrix}\dot{x_1} \\\dot{x_2} \\\dot{x_3} \\\dot{x_4}\end{bmatrix}=\begin{bmatrix}0 & 1 &0 &0 \\\frac{3(M+m)g}{(4M+m)l} &0 &0 &0 \\0 &0 &0 & 1\\-\frac{3mg}{4M+m} &0 &0 &0\end{bmatrix}\begin{bmatrix}x_1 \\x_2 \\x_3 \\x_4\end{bmatrix}+\begin{bmatrix}0 \\-\frac{3}{(4M+m)l} \\0 \\\frac{4}{4M+m}\end{bmatrix}F ⎣⎢⎢⎡x1˙x2˙x3˙x4˙⎦⎥⎥⎤=⎣⎢⎢⎡0(4M+m)l3(M+m)g0−4M+m3mg100000000010⎦⎥⎥⎤⎣⎢⎢⎡x1x2x3x4⎦⎥⎥⎤+⎣⎢⎢⎡0−(4M+m)l304M+m4⎦⎥⎥⎤F
输出变量选择为
y 1 = x y_1=x y1=x
y 2 = θ y_2=θ y2=θ
则输出方程为
y = [ x θ ] = [ 0 0 1 0 1 0 0 0 ] [ x 1 x 2 x 3 x 4 ] y=\begin{bmatrix}x\\θ\end{bmatrix}=\begin{bmatrix}0 &0 &1 &0\\1&0&0&0\end{bmatrix} \begin{bmatrix}x_1\\x_2\\x_3\\x_4\end{bmatrix} y=[xθ]=[01001000]⎣⎢⎢⎡x1x2x3x4⎦⎥⎥⎤
有:
A = [ 0 1 0 0 3 ( M + m ) ( 4 M + m ) l g 0 0 0 0 0 0 1 − 3 m g 4 M + m 0 0 0 ] A=\begin{bmatrix}0 & 1 &0 &0 \\\frac{3(M+m)}{(4M+m)l}g &0 &0 &0 \\0 &0 &0 & 1\\-\frac{3mg}{4M+m} &0 &0 &0\end{bmatrix} A=⎣⎢⎢⎡0(4M+m)l3(M+m)g0−4M+m3mg100000000010⎦⎥⎥⎤
B = [ 0 − 3 ( 4 M + m ) l 0 4 4 M + m ] B=\begin{bmatrix}0 \\-\frac{3}{(4M+m)l} \\0 \\\frac{4}{4M+m}\end{bmatrix} B=⎣⎢⎢⎡0−(4M+m)l304M+m4⎦⎥⎥⎤
C = [ 0 0 1 0 1 0 0 0 ] C=\begin{bmatrix}0 &0 &1 &0\\1&0&0&0\end{bmatrix} C=[01001000]
D = 0 D=0 D=0
传递矩阵
传递函数和状态空间方程之间可以进行转换。
由状态空间方程,根据公式,可以算得传递矩阵
![]()
可得
G ( s ) = [ 0 0 1 0 1 0 0 0 ] ( [ s 0 0 0 0 s 0 0 0 0 s 0 0 0 0 s ] − [ 0 1 0 0 3 ( M + m ) ( 4 M + m ) l g 0 0 0 0 0 0 1 − 3 m g 4 M + m 0 0 0 ] ) − 1 [ 0 − 3 ( 4 M + m ) l 0 4 4 M + m ] G(s)=\begin{bmatrix}0 &0 &1 &0\\1&0&0&0\end{bmatrix}\left(\begin{bmatrix}s &0 &0 &0 \\0 &s &0 &0 \\0 & 0 & s &0 \\0 &0 &0 &s\end{bmatrix}-\begin{bmatrix}0 & 1 &0 &0 \\\frac{3(M+m)}{(4M+m)l}g &0 &0 &0 \\0 &0 &0 & 1\\-\frac{3mg}{4M+m} &0 &0 &0\end{bmatrix}\right)^{-1}\begin{bmatrix}0 \\-\frac{3}{(4M+m)l} \\0 \\\frac{4}{4M+m}\end{bmatrix} G(s)=[01001000]⎝⎜⎜⎛⎣⎢⎢⎡s0000s0000s0000s⎦⎥⎥⎤−⎣⎢⎢⎡0(4M+m)l3(M+m)g0−4M+m3mg100000000010⎦⎥⎥⎤⎠⎟⎟⎞−1⎣⎢⎢⎡0−(4M+m)l304M+m4⎦⎥⎥⎤
使用matlab计算
%% 状态空间模型
syms M m l g;
A = [0 1 0 0 ;
3*(M+m)/(4*M+m)/l*g 0 0 0;
0 0 0 1;
-3*m*g/(4*M+m) 0 0 0;]
B = [0;
-3/(4*M+m)/l;
0;
4/(4*M+m);]
C = [0 0 1 0;
1 0 0 0;];
D = 0;
syms s;
si = s*eye(4);
%det(si-A);%行列式
%inv(si-A)%逆矩阵
Gs_z = C * inv(si-A) * B+D %转递矩阵
结果为:
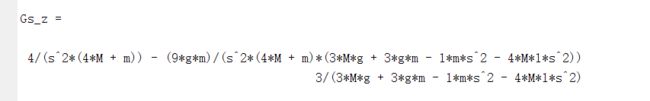
即小车位移和力的传递函数为第一行,摆杆摆角和驱动力的传递函数为第二行,我们关心摆角,则有
Θ ( s ) F ( s ) = − 3 ( 4 M + m ) l s 2 − 3 ( M + m ) g ( 4 M + m ) l \frac{Θ(s)}{F(s)}=\frac{-\frac{3}{(4M+m)l}}{s^2-\frac{3(M+m)g}{(4M+m) l}} F(s)Θ(s)=s2−(4M+m)l3(M+m)g−(4M+m)l3
可见和通过拉氏变换得到的传递函数一样。
Step 4:模型分析
分析模型是否稳定,可不可控,以及能不能观测。
稳定性
a. 奈奎斯特判据
使用matlab做出开环传递函数的零极点图和nyquist图
%% 模型分析
figure() ;
subplot(121);
pzmap(GS)%零极点图
grid;
subplot(122);
nyquist(GS)%nyquist图 由开环传递函数判断闭环系统稳定性 是图解分析的方法
grid;

由经典控制理论奈奎斯特判据,稳定系统在 s s s右半平面不能有闭环极点,公式为 Z = N + P = 0 Z=N+P=0 Z=N+P=0,从图中看到开环传递函数在 s s s右半平面内的极点数为 P = 1 P=1 P=1,对 − 1 + j 0 -1+j0 −1+j0顺时针包围的次数 N = 0 N=0 N=0,所以 Z = 1 Z=1 Z=1,即闭环传递函数特征方程的零点在s右半平面的个数为1,因此系统不稳定。
b. 李雅普诺夫第一法(间接法)
参考文献:现代控制理论 6-1 概念 6-2 李雅普诺夫第一法(间接法)
由现代控制理论李雅普诺夫第一法,通过判断系统矩阵A的特征值来判断稳定性,令 ∣ λ E − A ∣ = 0 |λE-A|=0 ∣λE−A∣=0,解得特征值 λ = [ 0 , 0 , 4.4294 , − 4.4294 ] λ=[0, 0, 4.4294, -4.4294] λ=[0,0,4.4294,−4.4294],有大于0的特征值,所以系统不稳定。matlab代码如下:
%李雅普诺夫第一法(间接法)
sys lm;%矩阵A特征值
da=det(lm*eye(4)-A) %A特征方程行列式
lm=solve(da)%求解da零点
%公式求解 和上面一样
eig(A) %公式求解A特征值
可控性
根据现代控制理论,完全可控的条件是 n × n n\times n n×n维的可控性矩阵 [ B , A B , . . . , A n − 1 B ] [B, AB, ...,A^{n-1} B] [B,AB,...,An−1B]的秩为 n n n,秩就是矩阵的非零子式的最高阶次。
本系统中,可控性矩阵为
Q c = [ A , A B , A 2 B , A 3 B ] Q_c=[A,AB,A^2B,A^3B] Qc=[A,AB,A2B,A3B]
在Matlab中计算
%% 可控可观性分析
qc=[B A*B A^2*B A^3*B]
rank(qc)%求秩
可观性
根据现代控制理论,完全可观的条件为 n × m n n\times mn n×mn维的可观测矩阵 [ C , C A , . . . , C A n − 1 ] T [C,CA,...,CA^{n-1}]^T [C,CA,...,CAn−1]T的秩等于 n n n,则本系统可观性矩阵为
G c = [ C C A C A 2 C A 3 ] G_c=\begin{bmatrix}\\C\\CA\\CA^2\\CA^3\end{bmatrix} Gc=⎣⎢⎢⎡CCACA2CA3⎦⎥⎥⎤
在Matlab中计算
gc=[C C*A C*A^2 C*A^3]';
rank(gc)%可观性矩阵求秩
Step 5: Simulink模型
代码分享
%% 清理
clear;
close;
clc;
%% 模型数据
M=1;%kg,小车质量
m=0.5;%kg,摆杆质量
l=0.5;%m,摆杆长
g=9.81;
%% 传递函数模型
num = [-3/((4*M+m)*l)]; %分子多项式系数行向量
den = [1 0 -(3*(M+m)*g)/((4*M+m)*l)]; %分母多项式系数行向量
GS = tf(num,den); %建立传递函数模型
%% 状态空间模型
%syms M m l g; %算符号传递矩阵时用上
A = [0 1 0 0 ;
3*(M+m)/(4*M+m)/l*g 0 0 0;
0 0 0 1;
-3*m*g/(4*M+m) 0 0 0;];
B = [0;
-3/(4*M+m)/l;
0;
4/(4*M+m);];
C = [0 0 1 0;
1 0 0 0;];
D = [0;0];
syms s;
si = s*eye(4);
%det(si-A);%行列式
%inv(si-A)%逆矩阵
Gs_z = C * inv(si-A) * B+D; %转递矩阵
%[num,den] = ss2tf(A,B,C,D,1)%也可使用此函数进行转换
GSS=ss(A,B,C,D)%由状态空间构造传递函数
%% 模型相关分析作图
sys1=feedback(GS,1);%闭环传递函数
figure()
rlocus(sys1)%根轨迹图 %由闭环传递函数特征方程的根随开环增益K从0-anf变化在S平面上
%的变化轨迹,优点在于不必求解特征方程
%全为复
%rlocus(A,B,C,D)%用户自定义K可以使用rlocus(sys1,K),rlocus(A,B,C,D,K)
figure();
bode(sys1);%伯德图
grid;
figure();
step(GS);%阶跃响应曲线
grid;
%% 稳定性分析
%nyquist判据方法
figure() ;
subplot(121);
pzmap(GS)%零极点图
grid;
subplot(122);
nyquist(GS)%nyquist图 由开环传递函数判断闭环系统稳定性 是图解分析的方法
grid;
%李雅普诺夫第一法(间接法)
syms lm;%矩阵A特征值
da=det(lm*eye(4)-A); %A特征方程行列式
lm=solve(da);%求解da零点
%公式求解 和上面一样
eigs(A) %公式求解A特征值
%% 可控可观性分析
qc=[B A*B A^2*B A^3*B];
rank(qc)%可控性矩阵求秩
gc=[C C*A C*A^2 C*A^3]';
rank(gc)%可观性矩阵求秩;
%%
交流群
感兴趣同学可加机械&自动化攻城狮交流群(群号:1105076200)

分享一下控制理论结构图,来源知乎
参考文献
[1] 倒立摆状态反馈控制——分析、建模与仿真(matlab)
[2] 《现代控制工程》 第五版 卢伯英译
[3] 《Matlab/Simulink 机电系统建模与仿真》宋志安
[4]王强. 直线倒立摆的起摆和稳摆智能控制研究[D].天津理工大学,2013.