Codeforces Round #598 (Div. 3)

Codeforces Round #598 (Div. 3)

比赛传送门

A - Payment Without Change

Problem Description

You have a coins of value n and b coins of value 1. You always pay in exact change, so you want to know if there exist such x and y that if you take x (0≤x≤a) coins of value n and y (0≤y≤b) coins of value 1, then the total value of taken coins will be S.
You have to answer q independent test cases.

Input

The first line of the input contains one integer q (1≤q≤10e4) — the number of test cases. Then q test cases follow.
The only line of the test case contains four integers a, b, n and S (1≤a,b,n,S≤10e9) — the number of coins of value n, the number of coins of value 1, the value n and the required total value.

Output

For the i-th test case print the answer on it — YES (without quotes) if there exist such x and y that if you take x coins of value n and y coins of value 1, then the total value of taken coins will be S, and NO otherwise.
You may print every letter in any case you want (so, for example, the strings yEs, yes, Yes and YES will all be recognized as positive answer).

Example

input
4
1 2 3 4
1 2 3 6
5 2 6 27
3 3 5 18
output
YES
NO
NO
YES

Code

#include 
 
using namespace std;
 
typedef long long ll;
 
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
 
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int a,b,n,s;
        scanf("%d%d%d%d",&a,&b,&n,&s);
        int need=s/n;
        int mon=0;
        if(need<=a)
            mon=n*need;
        else
            mon=n*a;
        if(s-mon<=b)
            cout<<"YES"<<endl;
        else
            cout<<"NO"<<endl;
    }
    return 0;
}

---

B - Minimize the Permutation

Problem Description

You are given a permutation of length n. Recall that the permutation is an array consisting of n distinct integers from 1 to n in arbitrary order. For example, [2,3,1,5,4] is a permutation, but [1,2,2] is not a permutation (2 appears twice in the array) and [1,3,4] is also not a permutation (n=3 but there is 4 in the array).
You can perform at most n−1 operations with the given permutation (it is possible that you don’t perform any operations at all). The i-th operation allows you to swap elements of the given permutation on positions i and i+1. Each operation can be performed at most once. The operations can be performed in arbitrary order.
Your task is to find the lexicographically minimum possible permutation obtained by performing some of the given operations in some order.
You can see the definition of the lexicographical order in the notes section.
You have to answer q independent test cases.
For example, let’s consider the permutation [5,4,1,3,2]. The minimum possible permutation we can obtain is [1,5,2,4,3] and we can do it in the following way:
perform the second operation (swap the second and the third elements) and obtain the permutation [5,1,4,3,2];
perform the fourth operation (swap the fourth and the fifth elements) and obtain the permutation [5,1,4,2,3];
perform the third operation (swap the third and the fourth elements) and obtain the permutation [5,1,2,4,3].
perform the first operation (swap the first and the second elements) and obtain the permutation [1,5,2,4,3];
Another example is [1,2,4,3]. The minimum possible permutation we can obtain is [1,2,3,4] by performing the third operation (swap the third and the fourth elements).

Input

The first line of the input contains one integer q (1≤q≤100) — the number of test cases. Then q test cases follow.
The first line of the test case contains one integer n (1≤n≤100) — the number of elements in the permutation.
The second line of the test case contains n distinct integers from 1 to n — the given permutation.

Output

For each test case, print the answer on it — the lexicograhically minimum possible permutation obtained by performing some of the given operations in some order.

Example

input
4
5
5 4 1 3 2
4
1 2 4 3
1
1
4
4 3 2 1
output
1 5 2 4 3
1 2 3 4
1
1 4 3 2

Note

Recall that the permutation p of length n is lexicographically less than the permutation q of length n if there is such index i≤n that for all j from 1 to i−1 the condition pj=qj is satisfied, and pi p=[1,3,5,2,4] is less than q=[1,3,5,4,2] (such i=4 exists, that pi p=[1,2] is less than q=[2,1] (such i=1 exists, that pi

Code

#include 
 
using namespace std;
 
typedef long long ll;
 
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
 
const int N=105;
 
int num[N];
int vis[N];
 
void init()
{
    memset(vis,0,sizeof(vis));
    vis[0]=1;
}
 
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        init();
        int n;
        scanf("%d",&n);
        rep(i,1,n)
        {
            scanf("%d",&num[i]);
        }
        int cnt=0;
        int minn=1;
        while(cnt<n-1&&minn!=n+1)
        {
            int p=1;
            rep(i,1,n)
            {
                if(num[i]==minn)
                {
                    p=i;
                    break;
                }
            }
            while(vis[p-1]==0&&num[p-1]>num[p])
            {
                swap(num[p],num[p-1]);
                vis[p-1]=1;
                cnt++;
                p--;
            }
            minn++;
        }
        rep(i,1,n)
        {
            printf("%d ",num[i]);
        }
        printf("\n");
    }
    return 0;
}

---

C - Platforms Jumping

Problem Description

There is a river of width n. The left bank of the river is cell 0 and the right bank is cell n+1 (more formally, the river can be represented as a sequence of n+2 cells numbered from 0 to n+1). There are also m wooden platforms on a river, the i-th platform has length ci (so the i-th platform takes ci consecutive cells of the river). It is guaranteed that the sum of lengths of platforms does not exceed n.
You are standing at 0 and want to reach n+1 somehow. If you are standing at the position x, you can jump to any position in the range [x+1;x+d]. However you don’t really like the water so you can jump only to such cells that belong to some wooden platform. For example, if d=1, you can jump only to the next position (if it belongs to the wooden platform). You can assume that cells 0 and n+1 belong to wooden platforms.
You want to know if it is possible to reach n+1 from 0 if you can move any platform to the left or to the right arbitrary number of times (possibly, zero) as long as they do not intersect each other (but two platforms can touch each other). It also means that you cannot change the relative order of platforms.
Note that you should move platforms until you start jumping (in other words, you first move the platforms and then start jumping).
For example, if n=7, m=3, d=2 and c=[1,2,1], then one of the ways to reach 8 from 0 is follow:

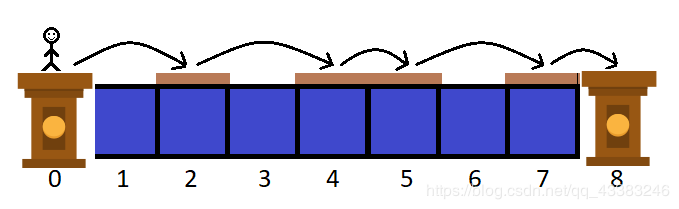
The first example: n=7.

Input

The first line of the input contains three integers n, m and d (1≤n,m,d≤1000,m≤n) — the width of the river, the number of platforms and the maximum distance of your jump, correspondingly.
The second line of the input contains m integers c1,c2,…,cm (1≤ci≤n,∑i=1mci≤n), where ci is the length of the i-th platform.

Output

If it is impossible to reach n+1 from 0, print NO in the first line. Otherwise, print YES in the first line and the array a of length n in the second line — the sequence of river cells (excluding cell 0 and cell n+1).
If the cell i does not belong to any platform, ai should be 0. Otherwise, it should be equal to the index of the platform (1-indexed, platforms are numbered from 1 to m in order of input) to which the cell i belongs.
Note that all ai equal to 1 should form a contiguous subsegment of the array a of length c1, all ai equal to 2 should form a contiguous subsegment of the array a of length c2, …, all ai equal to m should form a contiguous subsegment of the array a of length cm. The leftmost position of 2 in a should be greater than the rightmost position of 1, the leftmost position of 3 in a should be greater than the rightmost position of 2, …, the leftmost position of m in a should be greater than the rightmost position of m−1.
See example outputs for better understanding.

Examples

input
7 3 2
1 2 1
output
YES
0 1 0 2 2 0 3

input
10 1 11
1
output
YES
0 0 0 0 0 0 0 0 0 1

input
10 1 5
2
output
YES
0 0 0 0 1 1 0 0 0 0

Note

Consider the first example: the answer is [0,1,0,2,2,0,3]. The sequence of jumps you perform is 0→2→4→5→7→8.
Consider the second example: it does not matter how to place the platform because you always can jump from 0 to 11.
Consider the third example: the answer is [0,0,0,0,1,1,0,0,0,0]. The sequence of jumps you perform is 0→5→6→11.

Code

#include 
 
using namespace std;
 
typedef long long ll;
 
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
 
const int N=1005;
 
int a[N];
int ans[N];
 
int main()
{
    int n,m,d;
    scanf("%d%d%d",&n,&m,&d);
    int sum=0;
    rep(i,1,m)
    {
        scanf("%d",&a[i]);
        sum+=a[i];
    }
    int p=d;
    int cnt=1;
    while(p<=n-sum&&cnt<=m)
    {
        rep(i,0,a[cnt]-1)
        {
            ans[p+i]=cnt;
        }
        sum-=a[cnt];
        p+=d+a[cnt]-1;
        cnt++;
    }
    if(cnt==m+1&&p<=n)
    {
        printf("NO\n");
        return 0;
    }
    printf("YES\n");
    int pos=n;
    per(i,m,cnt)
    {
        rep(j,0,a[i]-1)
        {
            ans[pos--]=i;
        }
    }
    rep(i,1,n)
    {
        printf("%d ",ans[i]);
    }
    printf("\n");
    return 0;
}

---

D - Binary String Minimizing

Problem Description

You are given a binary string of length n (i. e. a string consisting of n characters ‘0’ and ‘1’).
In one move you can swap two adjacent characters of the string. What is the lexicographically minimum possible string you can obtain from the given one if you can perform no more than k moves? It is possible that you do not perform any moves at all.
Note that you can swap the same pair of adjacent characters with indices i and i+1 arbitrary (possibly, zero) number of times. Each such swap is considered a separate move.
You have to answer q independent test cases.

Input

The first line of the input contains one integer q (1≤q≤104) — the number of test cases.
The first line of the test case contains two integers n and k (1≤n≤106,1≤k≤n2) — the length of the string and the number of moves you can perform.
The second line of the test case contains one string consisting of n characters ‘0’ and ‘1’.
It is guaranteed that the sum of n over all test cases does not exceed 106 (∑n≤106).

Output

For each test case, print the answer on it: the lexicographically minimum possible string of length n you can obtain from the given one if you can perform no more than k moves.

Example

input
3
8 5
11011010
7 9
1111100
7 11
1111100
output
01011110
0101111
0011111

Note

In the first example, you can change the string as follows:
In the third example, there are enough operations to make the string sorted.

Code

#include 
 
using namespace std;
 
typedef long long ll;
 
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
 
const int N=1e6+5;
 
char str[N];
 
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int n;
        ll k;
        scanf("%d%I64d",&n,&k);
        scanf("%s",str+1);
        int zero=0;
        rep(i,1,n)
        {
            if(str[i]=='0')
            {
                if(k<i-zero-1)
                {
                   swap(str[i],str[i-k]);
                   break;
                }
                else
                {
                    swap(str[i],str[zero+1]);
                    k-=i-zero-1;
                    zero++;
                }
            }
        }
        printf("%s\n",str+1);
    }
    return 0;
}

---

E - Yet Another Division Into Teams

Problem Description

There are n students at your university. The programming skill of the i-th student is ai. As a coach, you want to divide them into teams to prepare them for the upcoming ICPC finals. Just imagine how good this university is if it has 2⋅105 students ready for the finals!
Each team should consist of at least three students. Each student should belong to exactly one team. The diversity of a team is the difference between the maximum programming skill of some student that belongs to this team and the minimum programming skill of some student that belongs to this team (in other words, if the team consists of k students with programming skills a[i1],a[i2],…,a[ik], then the diversity of this team is maxj=1ka[ij]−minj=1ka[ij]).
The total diversity is the sum of diversities of all teams formed.
Your task is to minimize the total diversity of the division of students and find the optimal way to divide the students.

Input

The first line of the input contains one integer n (3≤n≤2⋅105) — the number of students.
The second line of the input contains n integers a1,a2,…,an (1≤ai≤109), where ai is the programming skill of the i-th student.

Output

In the first line print two integers res and k — the minimum total diversity of the division of students and the number of teams in your division, correspondingly.
In the second line print n integers t1,t2,…,tn (1≤ti≤k), where ti is the number of team to which the i-th student belong.
If there are multiple answers, you can print any. Note that you don’t need to minimize the number of teams. Each team should consist of at least three students.

Examples

input
5
1 1 3 4 2
output
3 1
1 1 1 1 1

input
6
1 5 12 13 2 15
output
7 2
2 2 1 1 2 1

input
10
1 2 5 129 185 581 1041 1909 1580 8150
output
7486 3
3 3 3 2 2 2 2 1 1 1

Note

In the first example, there is only one team with skills [1,1,2,3,4] so the answer is 3. It can be shown that you cannot achieve a better answer.
In the second example, there are two teams with skills [1,2,5] and [12,13,15] so the answer is 4+3=7.
In the third example, there are three teams with skills [1,2,5], [129,185,581,1041] and [1580,1909,8150] so the answer is 4+912+6570=7486.

题意

给定n个人的能力值，每个人有一个能力值，整个队伍的一个我也不知道叫啥的值为一个队伍里最大能力值减最小能力值，一支队最少三人，问最下的能力值之和是多少。

思路

我们可以发现，每支队伍的人数只能为3、4、5，所以我们可以直接dp求解。
然后dp的同时用一个last数组记录这个dp值是由那个dp值传过来的，即可记录路径。

坑点

反正我是没想到每个队伍的人数只能为3、4、5。

Code

#include 
 
using namespace std;
 
typedef long long ll;
 
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
 
const int N=2e5+5;
 
struct S
{
    int num;
    int id;
    int team;
} peo[N];
 
bool cmp_num(S aa,S bb)
{
    return aa.num<bb.num;
}
 
bool cmp_id(S aa,S bb)
{
    return aa.id<bb.id;
}
 
int last[N];
int dp[N];
 
int main()
{
    int n;
    scanf("%d",&n);
    ll sum=0;
    rep(i,1,n)
    {
        scanf("%d",&peo[i].num);
        peo[i].id=i;
    }
    sort(peo+1,peo+1+n,cmp_num);
    sum=peo[n].num-peo[1].num;
    if(n<=5)
    {
        printf("%d %d\n",peo[n].num-peo[1].num,1);
        rep(i,1,n)
        {
            printf("1 ");
        }
        printf("\n");
        return 0;
    }
    rep(i,0,n)
    {
        dp[i]=sum;
    }
    last[0]=-1;
    dp[0]=INT_MAX;
    dp[1]=INT_MAX;
    dp[2]=INT_MAX;
    dp[3]-=peo[4].num-peo[3].num;
    last[3]=0;
    dp[4]-=peo[5].num-peo[4].num;
    last[4]=0;
    dp[5]-=peo[6].num-peo[5].num;
    last[5]=0;
    peo[n+1].num=peo[n].num;
    rep(i,6,n)
    {
        int p=i-3;
        int minn=0x3f3f3f3f;
        if(dp[i-3]<dp[i-4])
        {
            minn=dp[i-3];
            p=i-3;
        }
        else
        {
            minn=dp[i-4];
            p=i-4;
        }
        if(dp[i-5]<minn)
        {
            minn=dp[i-5];
            p=i-5;
        }
        dp[i]=minn-(peo[i+1].num-peo[i].num);
        last[i]=p;
    }
    int cnt=1;
    int pos=n;
    while(last[pos]!=-1)
    {
        peo[pos].team=cnt;
        cnt++;
        pos=last[pos];
    }
    int cntt=0;
    per(i,n,1)
    {
        if(peo[i].team==0)
        {
            peo[i].team=cntt;
        }
        else
        {
            cntt=peo[i].team;
        }
    }
    sort(peo+1,peo+1+n,cmp_id);
    printf("%d %d\n",dp[n],cntt);
    rep(i,1,n)
    {
        printf("%d ",peo[i].team);
    }
    printf("\n");
    return 0;
}

---

F - Equalizing Two Strings

Problem Description

You are given two strings s and t both of length n and both consisting of lowercase Latin letters.
In one move, you can choose any length len from 1 to n and perform the following operation:
Choose any contiguous substring of the string s of length len and reverse it;
at the same time choose any contiguous substring of the string t of length len and reverse it as well.
Note that during one move you reverse exactly one substring of the string s and exactly one substring of the string t.
Also note that borders of substrings you reverse in s and in t can be different, the only restriction is that you reverse the substrings of equal length. For example, if len=3 and n=5, you can reverse s[1…3] and t[3…5], s[2…4] and t[2…4], but not s[1…3] and t[1…2].
Your task is to say if it is possible to make strings s and t equal after some (possibly, empty) sequence of moves.
You have to answer q independent test cases.

Input

The first line of the input contains one integer q (1≤q≤104) — the number of test cases. Then q test cases follow.
The first line of the test case contains one integer n (1≤n≤2⋅10⁵) — the length of s and t.
The second line of the test case contains one string s consisting of n lowercase Latin letters.
The third line of the test case contains one string t consisting of n lowercase Latin letters.
It is guaranteed that the sum of n over all test cases does not exceed 2⋅105 (∑n≤2⋅10⁵).

Output

For each test case, print the answer on it — “YES” (without quotes) if it is possible to make strings s and t equal after some (possibly, empty) sequence of moves and “NO” otherwise.

Example

input
4
4
abcd
abdc
5
ababa
baaba
4
asdf
asdg
4
abcd
badc
output
NO
YES
NO
YES

题意

给定两个长度为n的串s和t，每次操作可以在s和t中分别选择长度相同（位置可以不同）的串进行反转操作，问能不能在若干次操作之后，使得两个串完全相同。

思路

1.如果两个串中各个字符出现的次数不同，输出NO
2.如果两个串中某个字符出现的次数大于等于2，输出YES。
3.如果两个串中逆序对的个数的奇偶性不同输出NO，否则输出YES。

详解：
2.如果两个串中某个字符出现的次数大于等于2，我们可以先将这个字符全部移到串的最前端，然后一个串始终调换这两个相同的字符，后面的字符按照冒泡排序的方法跟另一个串对比排好即可。
3.一个串中选择长度为len的串进行反转之后，串的逆序对的个数的奇偶性不变。如果奇偶性相同，一个串始终反转某两个字符，另一个串按照冒泡排序的方式对比排好即可。

坑点

一开始以为是O(n²)的复杂度，然鹅n是2e5啊，4e10了啊,CF再牛逼1s也不能1e10吧。
但是！
经过第2条的筛选之后，剩下的串每个字符出现的次数最多只有一次，也就是说字符串的长度最长为26，O(n²）的复杂度最坏情况就是O(26²)。。。
所以这样并没有什么毛病，复杂度还挺低。

Code

#include 
 
using namespace std;
 
typedef long long ll;
 
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
 
const int N = 2e5+5;
 
char str1[N],str2[N];
int vis1[30],vis2[30];
 
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        memset(vis1,0,sizeof(vis1));
        memset(vis2,0,sizeof(vis2));
        int n;
        scanf("%d",&n);
        scanf("%s%s",str1+1,str2+1);
        int flag=-1;
        rep(i,1,n)
        {
            vis1[str1[i]-'a']++;
            vis2[str2[i]-'a']++;
        }
        rep(i,0,28)
        {
            if(vis1[i]!=vis2[i])
                flag=0;
        }
        if(flag==0)
        {
            printf("NO\n");
            continue;
        }
        rep(i,0,28)
        {
            if(vis1[i]>=2)
                flag=1;
        }
        if(flag==1)
        {
            printf("YES\n");
            continue;
        }
        int cnt1=0,cnt2=0;
        rep(i,1,n)
        {
            rep(j,i,n)
            {
                if(str1[i]>str1[j])
                    cnt1++;
                if(str2[i]>str2[j])
                    cnt2++;
            }
        }
        if(cnt1%2==cnt2%2)
            printf("YES\n");
        else
            printf("NO\n");
    }
    return 0;
}