目录
1365A. Matrix Game
1365B. Trouble Sort
1365C. Rotation Matching
1365D. Solve The Maze
1365E. Maximum Subsequence Value
1365F. Swaps Again
1365A. Matrix Game
题意：给一个n*m的01矩阵，两人轮流将0转化为1，若点pos可以被转化，那么要求x行和y列没有1。谁不能转谁输。
思路：计算所有满足的点的数量，根据奇偶性判断。
AC代码：
/*---------------------------------
*File name: A.cpp
*Creation date: 2020-06-07 22:28
*Link:
*-------------------------------*/
#include
#include
1365B. Trouble Sort
题意：给长度为为n的数组，每个数拥有属性（0或1），问是否能够将数组通过swap操作变为非递减数组，交换的两个数的属性必须不相同。
思路：想想就可以明白如果要排序属性为0的，只要有一个1 存在，就可以用这个1作为媒介交换两个0，反之也是这样，因此如果属性1和属性0的数都有，必定可以排序。如果0或1没有，那么直接判断原数组是否是非递减序列。
AC代码：
/*---------------------------------
*File name: A.cpp
*Creation date: 2020-06-07 23:17
*Link:
*-------------------------------*/
#include
#include
1365C. Rotation Matching
题意：给定两个排列，问能否通过左移右移操作将a序列和b序列相同数在同一位置的数量最多。左移右移操作定义为：对于序列c: 左移操作为将所有数循环地向左移动一个位置，即变为：c1:=c2,c2:=c3,…,cn:=c1。右移类似。
思路：因为是排列，所以每个数出现且只出现一次，那么对于b排列中的任意一个数x，记录下x在a排列中的位置，即是要将b中的x与a对齐所需要的操作次数。记录下每一个操作次数所能够对齐的数量，取max即是答案。
AC代码：
/*---------------------------------
*File name: A.cpp
*Creation date: 2020-06-07 23:41
*Link:
*-------------------------------*/
#include
#include
1365D. Solve The Maze
题意：给一个n*m的迷宫，里面有好人坏人和墙壁，问能不能通过增加墙壁使的所有好人能够到达出口而所有坏人不能。出口在点（n，m）。
思路：暴力找出所有坏人的位置，在他们四周放上墙壁，在过程中判断放墙壁的位置是否有好人，有的话则不行。若堵住了所有坏人且没有好人在坏人相邻的格子情况下，从出口BFS标记所有能到达出口的点，再暴力循环一遍找所有好人的位置，只要所有好人的位置都被标记，那么好人就可以到达出口，反之不行。
AC代码：
/*---------------------------------
*File name: A.cpp
*Creation date: 2020-06-07 23:17
*Link:
*-------------------------------*/
#include
#include
1365E. Maximum Subsequence Value
题意：有点难解释。。建议自己看题。我这里就粗略解释：给定一个数组a，要求选出具有最大价值的子序列。假设此子序列的长度为k，那么最大价值的计算方法为：对于这个序列中的所有数的二进制表示，第 i （从0开始）位上是1的数的数量若大于等max(k - 2, 1)，那么价值就可以 +=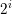 
。（还没理解的可以看看样例解释）。
思路：（赛后容易知道）子序列的选择其实长度最大为3，再大的话，就不仅仅对答案的贡献不大，还把答案的贡献缩小了。因为序列长度在3以内时都只需要1个数在第 i 位上是1就可以，若长度为4，那么可能会导致一些数位只有一个数满足，而要求的计算价值至少需要两个，这样有可能还会拖累到价值的计算，但是又不会给价值增加答案：对于本身第 i 位已经有1个的，若新增的数第 i 位也有1，对答案不会有增加，对本身第 i 位没有1的，新增的数第 i 位有1，也无法计入答案，因此选择三个以内是可以保证价值的最大化的。由于n只有500，所以可以暴力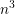
枚举所有方案，价值的计算就转化为了：对于第 i 位，若有1，则价值+=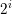。而第 i 位上是否有1，直接按位或就能知道枚举的3个数哪里有1了。
AC代码：
/*---------------------------------
*File name: E.cpp
*Creation date: 2020-06-08 08:25
*Link:
*-------------------------------*/
#include
#include
1365F. Swaps Again
题意：给定两个长度为N的数组a，b，问能否通过一定数量的操作使得数组A与数组B相等。操作为：选择一个L，将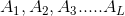
与
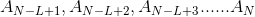交换位置。
思路：可以发现，不管怎么操作，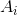
与
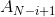始终相互对应，始终是对称的。所以只需要将A数组中的所有
与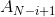的对应保存起来，与B数组的对应判断是否完全相同。如果相同则必定可以使得A数组成为B数组。
AC代码：
/*---------------------------------
*File name: A.cpp
*Creation date: 2020-07-04 14:18
*Link:
*-------------------------------*/
#include
#include
