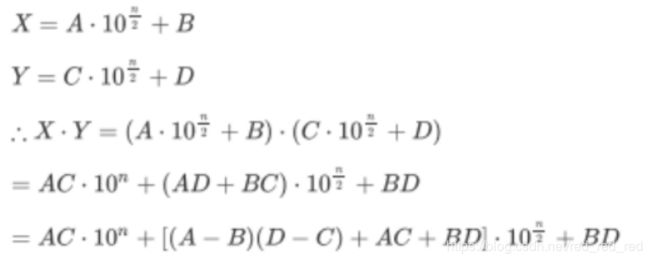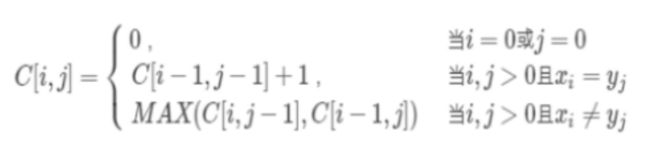计算机算法设计与分析(整理+代码)更新ing
一.递归与分治
1.大整数的乘法
将n位的整数分成两段,每段长度数 n/2
package algorithm_2019;
import java.math.BigInteger;
import java.util.Scanner;
public class 分治法求大整数乘法{
static Scanner cin = new Scanner(System.in);
static BigInteger Sign(BigInteger a) {//符号
if(a.compareTo(BigInteger.ZERO) > 0)
return BigInteger.ONE;
else return BigInteger.valueOf(-1);
}
static int Max(int a,int b) {//比较大小
if(a>b) return a;
else return b;
}
static BigInteger multi(BigInteger a,BigInteger b,int len_a,int len_b) {
BigInteger sign = Sign(a).multiply(Sign(b));
a = a.abs();
b = b.abs();
if(a.compareTo(BigInteger.ZERO) == 0 || b.compareTo(BigInteger.ZERO) == 0)
return BigInteger.ZERO;
else if(len_a == 1 || len_b == 1)
return sign.multiply(a.multiply(b));
else {
int half = Max(len_a,len_b) / 2;
int lena = len_a - half;
int lenb = len_b - half;
BigInteger tmp1 = BigInteger.valueOf(10).pow(half);
BigInteger tmp2 = BigInteger.valueOf(10).pow(2*half);
BigInteger A = a.divide(tmp1);
BigInteger B = a.mod(tmp1);
BigInteger C = b.divide(tmp1);
BigInteger D = b.mod(tmp1);
BigInteger AC = multi(A,C,lena,lenb);
BigInteger BD = multi(B,D,half,half);
BigInteger num1 = A.subtract(B);
BigInteger num2 = D.subtract(C);
int len1 = num1.abs().toString().length();
int len2 = num2.abs().toString().length();
BigInteger ABCD = multi(num1,num2,len1,len2).add(AC).add(BD);
return sign.multiply(AC.multiply(tmp2).add(ABCD.multiply(tmp1)).add(BD));
}
}
public static void main(String[] args) {
BigInteger a = cin.nextBigInteger();
BigInteger b = cin.nextBigInteger();
String str_a = a.toString();
String str_b = b.toString();
System.out.println("分治法求大整数乘法:\n"+multi(a,b,str_a.length(),str_b.length()));
}
}2.Strassen矩阵乘法
3.棋盘覆盖
4.合并排序
递归的实现:
算法设计的思想就是,将一个大的序列划分成两个小的左右序列,然后这样递归下去,先完成小的序列的有序化,再将两个有序化的小的序列合并,完成大的序列的有序化。这里需要注意的就是在将两个有序的子数组有序的合并到一起的时候,可能某个子数组会有剩下的元素,没有被转移到新数组中,这里就需要在最后加上一个判断,来将两个子数组中可能剩下的元素都转移到新数组中
void merge_sort(vector &a,int l,int r){
if(l>=r)
return;
int mid=(l+r)/2;
merge_sort(a,l,mid);
merge_sort(a,mid+1,r);//左半部分和右半部分排序
static vector w;
w.clear();
int i=l,j=mid+1;
while(i<=mid&&j<=r){//将两个有序数组合并
if(a[i]<=a[j])
w.push_back(a[i++]);
else
w.push_back(a[j++]);
}
while(i<=mid) w.push_back(a[i++]);//余下的部分添加到最后
while(j<=r) w.push_back(a[j++]);
for(int i=l,j=0;j 非递归的实现:
归并排序的非递归的实现就是不将数组划分,而是直接先将数组a 中相邻元素两两配对,用合并算法将他们排序,构成n/2组长度为2的排好序的子数组段,再将他们排序成长度为4的排好序的子数组段,如此下去,直至整个数组排好序
#include
using namespace std;
template
void Merge(T a[], T p[], int l, int m, int r){
int left = l, j = m + 1, k = l;
while ((left <= m) && (j <= r)){
if (a[left] <= a[j])
p[k++] = a[left++];
else
p[k++] = a[j++];
}
if (left > m)
for (int q = j; q <= r; q++)
p[k++] = a[q];
if (j > r)
for (int q = left; q <= m; q++)
p[k++] = a[q];
}
template
void MergePass(T a[], T p[], int s, int b){
int i = 0;
while (i <= b - 2 * s){
Merge(a,p,i,i+s-1,i+2*s-1);
i = i + 2 * s;
}
if (i + s < b)
Merge(a,p,i,i+s-1,b-1);
else
for (int q = i; q < b; q++)
p[q] = a[q];
}
template
void MergeSort(T a[], int b){
T* p = new T[b];
int s = 1;
while (s < b){
MergePass(a,p,s,b);
s += s;
MergePass(p,a,s,b);
s += s;
}
}
int main(){
int m;
cin >> m;
int* a = new int[m];
for (int i = 0; i < m; i++)
cin >> a[i];
MergeSort(a, m);
for (int i = 0; i < m; i++)
cout << a[i] << ' ';
cout< 归并排序思想解决逆序对问题:
这里用到了归并的思想,你需要求出左边部分的逆序对数,然后求出右边部分的逆序对数,然后还要求出左半部分和右半部分汇总起来的时候的逆序对数,因为是和归并排序一样的实现,所以这个算法的时间复杂度是O(nlogn)。
需要注意的就是,在分别求出左边和右边的逆序对数的时候,还得再求出左右两部分的逆序对数量,因为这里是对数组进行从大到小的排序,当右半部分比左半部分的某个元素小的时候,它一定比左边元素后边的所有元素都小。
int find(vector &a,int l,int r){
if(l>=r)
return 0;
int res=0;
int mid=(l+r)/2;
res+=find(a,l,mid);//左
res+=find(a,mid+1,r);//右
static vector w;
w.clear();
int i=l,j=mid+1;
while(i<=mid&&j<=r){//交叉排序
if(a[i]<=a[j])
w.push_back(a[i++]);
else{
res+=mid-i+1;//!!! a[j] 比 a[i] 小的时候,一定也比后边的都小
w.push_back(a[j++]);
}
}
while(i<=mid) w.push_back(a[i++]);//剩余部分
while(j<=r) w.push_back(a[j++]);
for(int i=l,j=0;j 5.快速排序
def swap(a,b):
t=a
a=b
b=t
def QuickSort(a, l, r):
if l>r:
return -1
temp=a[l]
i=l
j=r
while i!=j:
while a[j]>=temp and i6.线性时间选择
7.最接近点对问题
8.循环赛日程表
void GameTable(int k){
int n=2;
a[1][1]=1;
a[1][2]=2;
a[2][1]=2;
a[2][2]=1;//预先把左上角设置好
for(int t=2;t分治法实现:
按分治策略,我们可以将所有的选手分为两半,则n个选手的比赛日程表可以通过n/2个选手的比赛日程表来决定。递归地用这种一分为二的策略对选手进行划分,直到只剩下两个选手时,比赛日程表的制定就变得很简单。这时只要让这两个选手进行比赛就可以了。如上图,所列出的正方形表是8个选手的比赛日程表。其中左上角与左下角的两小块分别为选手1至选手4和选手5至选手8前3天的比赛日程。据此,将左上角小块中的所有数字按其相对位置抄到右下角,又将左下角小块中的所有数字按其相对位置抄到右上角,这样我们就分别安排好了选手1至选手4和选手5至选手8在后4天的比赛日程。依此思想容易将这个比赛日程表推广到具有任意多个选手的情形
#include
using namespace std;
int pre[1005][1005];
void print(int n){
for(int i=0;i>k;
int n=1;
for(int i=1;i 二.动态规划
1.矩阵连乘问题
若使用穷举搜索法,其复杂度是随着n的增长呈指数增长的,可以使用动态规划的算法来解决,即求其最优子结构。
设Ai Ai+1…Aj记作A[i:j],设A[i:j] 1<=i <= j <= n,所需要的最少数乘次数为dp[i][j].则有:
dp[i][j] = 0, i = j;
dp[i][j] = min{dp[i][k] + dp[k+1][j] + pi-1*pk*pj }, i < j .(枚举k的位置)
path[][]用来记录最优解的位置,最后通过递归的方式,确定最后的计算次序。
#include
#include
using namespace std;
int p[1005];
int dp[1005][1005];
int path[1005][1005];
int n=5;
void Traceback(int i,int j){//输出路径
if(i==j)
return ;
Traceback(i,path[i][j]);
Traceback(path[i][j]+1,j);
cout<<"Multipaly A ("<>t;
while(t--){
for(int i=0;i<=n;i++){
cin>>p[i];
}
memset(dp,0,sizeof(dp));
memset(path,0,sizeof(path)); //初始化
for(int i=1;i<=n;i++){
dp[i][i]=0;
}
for(int r=2;r<=n;r++){//第几个对角线
for(int i=1;i<=n-r+1;i++){//对角线上的元素个数(上三角)
int j=i+r-1;
dp[i][j]=dp[i+1][j]+p[i-1]*p[i]*p[j];
path[i][j]=i;
for(int k=i+1;k 2.最长公共子序列
设序列X={X1,X2 ...... Xm}和Y={Y1,Y2.......Yn}的最长公共子序列为Z={Z1,Z2......Zk}则
从上述的结论可以看出,两个序列的最长公共子序列问题包含两个序列的前缀的最长公共子序列,因此,最长公共子序列问题具有最优子结构性质,在设计递归算法时,不难看出递归算法具有子问题重叠的性质
设C[i,j]表示Xi 和Yj 的最长公共子序列的长度,如果i=0或j=0即一个序列长度为0时,那么最长公共子序列的长度就是0,根据最长公共子序列问题的最优子结构的性质,可以有以下公式:
使用动态规划算法解决此问题,可采用从简单到复杂的方式进行计算。在计算的过程中,保存已解决的子问题答案。每个子问题只计算一次,而在后边需要时只需要简单的查一下,从而避免大量的重复计算。还是用了path数组存下了路径信息,在计算结束后可以采用递归的算法打印出最长公共子序列。
#include
#include
#include
using namespace std;
char x[1005],y[1005];
int dp[1005][1005];
int path[1005][1005];
int t;
void print_path(int i,int j){//打印路径
if(i==0||j==0)
return ;
if(path[i][j]==1){
print_path(i-1,j-1);
cout<>t;
while(t--){
scanf("%s%s",x,y);
memset(dp,0,sizeof(dp));
memset(path,0,sizeof(path));//初始化
int n=strlen(x);
int m=strlen(y);
for(int i=n;i>=0;i--)//将两个字符序列改成由下标1开始
x[i]=x[i-1];
for(int j=m;j>=0;j--)
y[j]=y[j-1];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(x[i]==y[j]){
dp[i][j]=dp[i-1][j-1]+1;
path[i][j]=1;
}
else if(dp[i-1][j]>=dp[i][j-1]){
dp[i][j]=dp[i-1][j];
path[i][j]=2;
}else{
dp[i][j]=dp[i][j-1];
path[i][j]=3;
}
}
}
cout< 3.最大字段和
#include
#include
using namespace std;
int n;
int a[1005],dp[1005];
int main(){
while(1){
cin>>n;
int Max=-1;
if(n==0) break;
for(int i=0;i>a[i];
if(a[0]<0) dp[0]=0;
else dp[0]=a[0];//处理第一个数
for(int i=1;i 4.图像压缩
5.0-1背包问题
6.最优二叉搜索树
三.贪心