迷宫问题求解
问题一:在迷宫中找到出口(只需找到一个即可)
给定一张迷宫地图和一个迷宫入口,然后进入迷宫探索找到一个出口。
问题分析:
1. 首先要有一张迷宫地图,地图由两部分组成:
(1)一是迷宫中各处的位置坐标,
(2)二是迷宫各位置处的状态信息,即该处是墙还是路
所以,该迷宫地图可由一个二维数组来表示。数组的横纵坐标表示迷宫各处的位置坐标,数组元素表示各位置处的状态信息。
在这里,规定:(1)迷宫地图是6*6的,即二维数组是6行6列的。(2)在迷宫中用0表示墙,用1表示路
因此,迷宫的地图刻画如下:
根据上述的描述,用下述代码初始化一张地图:
#define ROW 6//迷宫的行数
#define COL 6//迷宫的列数
//该结构体用于表示迷宫的地图,数组中存放墙和路
typedef struct Maze
{
int map[ROW][COL];
}Maze;
//初始化迷宫地图
void MazeInit(Maze* maze)
{
if(maze == NULL)
{
//非法输入
return;
}
//因为二维数组只有在初始化是才能对数组元素全部赋值
//在赋值时只能单个赋值
int temp[ROW][COL] =
{
{0,1,0,0,0,0},
{0,1,1,1,0,0},
{0,1,0,0,0,0},
{0,1,1,0,0,0},
{0,1,0,0,0,0},
{0,1,0,0,0,0}
};
int row = 0;
for(;row < ROW;++row)
{
int col = 0;
for(;col < COL;++col)
{
maze->map[row][col] = temp[row][col];
}
}
}
2. 然后从入口进入迷宫开始寻找出口
(1)要对迷宫进行探索,首先要知道迷宫各处的状态信息
(2)要知道入口点的位置才能进入迷宫。因为迷宫中各处的位置信息有行列两个位置坐标,需要用两个变量进行表示,所以为方便起见,将行列坐标封装在一个结构体中,用一个结构体变量来表示位置信息。
所以,在寻找出口的函数中需要用到两个参数,一是迷宫的地图,二是迷宫的入口点位置。因此函数头可以表示为:
//根据入口点和迷宫地图找迷宫的出口
void Path(Maze* maze,Point entry);其中:
该结构体用于表示迷宫各处的行,列坐标
typedef struct Point
{
int row;//横坐标
int col;//列坐标
}Point;Path函数是实现思路如下:
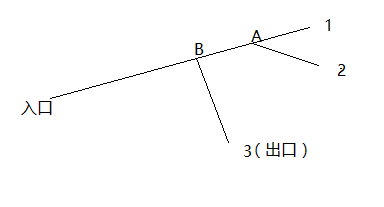
设想一下,在实际生活中,要去一个目的地。路线图如下:
首先从入口点开始,要沿着一条路走,走到某处时,发现一个岔路口B有两条路可以走。然后选择其中一条路BA往前走。之后发现又到了一个岔路口A,又有两条路可以走。选择路1继续往前走,发现该条路走不通了。此时,就要根据来时的路往回走,走到刚刚的岔路口A,然后选择另一条路2继续往前走,发现该条路又走不通了,再根据来时的路往前走到A,此时A的两条路都已经探索过了,发现都走不通。在根据来时的路往前走到B,选择另一条路3继续往前走,最后发现找到出口了。
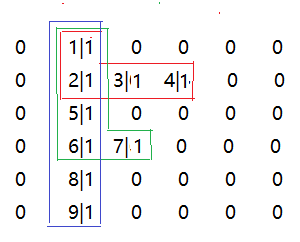
在迷宫中寻找出口也是这样的思路。如下图:
在上图中,一个位置有两个数字的第一个数字表示该处的位置序号,第二个数字表示该处实际的状态信息。上图中三种颜色框起来的数字表示的就是探索的三条路线。
(1)红色:首先从入口点1处进入。然后探索2,3,4,点4的四周点要么是墙,不能继续往前,要么已经走过(如点3),所以该条路:1->2->3->4走不通,此时需要回溯到点2处
(2)绿色:回到点2后,因为点2的上,右点已经探索过,所以接着探索点5,然后是6,7。点7处同样也走不通。即1->2->6->6->走不通,接着回溯到点6处
(3)蓝色:回到点6处后,因为点6的上,右点已经探测过,所以接着探索点8,然后是9。此时发现已经到出口了。说明沿着路:1->2->5->6->8->9便可以找到出口。
其中,要向沿着原路返回,就必须保存已经走过的路即已经走过的各点处的位置信息,所以可以利用栈的结构来实现。走过一处,将该处的位置信息入栈保存。走到某处发现路走不通了,就将该栈中的元素出栈回溯,然后原路返回。
对于栈结构的实现有两种方法:
(1)一是利用函数的调用栈。走过一个位置,将该位置放入函数的栈中,即需要调用一个函数来保存该位置信息。故需要不断的调用该函数。因此利用递归函数的调用栈来实现。当原路返回时,需要出栈,此时递归函数调用结束了,就相当于出栈了。
(2)手动设置一个栈结构。走过一个位置,将该位置压入设置的栈结构中。原路返回时,将栈顶元素一个个出栈即可。
下面利用上述两种方法来实现Path函数。
3. 利用函数的调用栈来实现Path函数
因为最初走过的位置必定是入口点,所以对入口点调用递归函数。实现如下:
//根据入口点找迷宫的出口
void Path(Maze* maze,Point entry)
{
if(maze == NULL)
{
//非法输入
return;
}
//从入口处开始探索,判断当前点是否满足继续走下去的要求
//需要一个递归辅助函数判断到当前点是否满足要求
_Path(maze,entry,entry);//其中第一个entry表示当前点的位置信息,第二个entry表示入口点的位置信息
return;
}
递归函数_Path函数的实现思路如下:
因为每经过一处,都要调用该递归函数,即将经过的位置入栈,但是该位置是否能走,还需要在进行判断。所以在递归函数函数中需要对各个位置进行判断:
(1)该位置能否落脚,如果不能落脚,就直接结束函数调用。表示不能沿着该位置往前走;
(2)如果能落脚,标记该位置(规定标记为2),表示走过了该位置。
(3)判断该位置是否是出口(规定出口在边界上),如果是出口,就说明找到出路了,直接打印信息并返回即可;
(4)如果不是出口,就探索该位置处的四周点(规定:沿着上,右,下,左顺时针方向进行深度优先探索)。将四周点作为新的当前点出入递归函数,进行函数调用。
(5)当四周点都已经探索完了,说明在该位置处的所有岔路都已经探索结束。所以需原路返回探索上一个岔路口的其他路线。此时,直接结束函数调用就表示将当前位置出栈了。
实现代码如下:
//递归辅助函数,不断判断当前点是否满足要求,来找到出口点
void _Path(Maze* maze,Point cur,Point entry)
{
if(maze == NULL)
{
//非法输入
return;
}
printf("(%d,%d)\n",cur.row,cur.col);
//1. 首先判断当前点能否落脚,如果当前点不能落脚,直接回溯出函数的调用栈
if(CanStay(maze,cur) == 0)
{
return;
}
//2. 如果能落脚,表示该位置可以走,就对其进行标记表示已经走过
Mark(maze,cur);
//3. 判断当前点是否是出口,如果是出口,说明找到了出口,直接打印消息返回即可
if(IsExit(cur,entry) == 1)
{
printf("找到一条出路\n");
return;
}
//4. 如果不是出口,就从当前的四周点进行深度优先探索(上,右,下,左顺时针进行)
Point up = cur;
up.row -= 1;
_Path(maze,up,entry);
Point right = cur;
right.col += 1;
_Path(maze,right,entry);
Point down = cur;
down.row += 1;
_Path(maze,down,entry);
Point left = cur;
left.col -= 1;
_Path(maze,left,entry);
//5. 如果四周点都已经探索完,就回溯探索其他的路
return;
}
其中,落脚点函数实现思路:
(1)如果当前位置处于地图之外,则不能落脚;
(2)如果当前位置处的值为0,说明是墙,也不能落脚;
(3)如果当前位置处的值为2,说明已经探索该点,所以不需要再次探索,因此也不能落脚
(4)如果当前位置处的值为1,说明是路也没有对其探索过,所以可以落脚。
代码实现如下:
//判断当前点能否落脚
int CanStay(Maze* maze,Point cur)
{
if(cur.row < 0 || cur.row >= ROW || cur.col < 0 || cur.col >= COL)
{
//当前点的位置在地图之外,所以不能落脚
return 0;
}
if(maze->map[cur.row][cur.col] == 1)
{
//说明是路,且是未走过的路,说明可以落脚
return 1;
}
else
{
return 0;
}
}
标记函数实现思路(规定将走过的路标记为2):
直接将该处的值标记为2,表示走过该位置即可。
代码实现如下:
//标记走过的路
void Mark(Maze* maze,Point cur)
{
if(maze == NULL)
{
//非法输入
return;
}
maze->map[cur.row][cur.col] = 2;
return;
}
出口判断函数实现思路(规定边界上的点都是出口点):
(1)首先入口点一定不是出口点(当前点是入口点时,它就处于边界上。但此时不是出口点)
(2)如果当前点的位置位于边界上,就说明当前点就是出口
代码实现如下:
//判断是否为出口点
int IsExit(Point cur,Point entry)
{
if(cur.row == entry.row && cur.col == entry.col)
{
//入口点不能为出口点
return 0;
}
if(cur.row == 0 || cur.row == ROW - 1 || cur.col == 0 || cur.col == COL - 1)
{
//当前点在边界上,说明是出口点
return 1;
}
else
{
return 0;
}
}4. 手动设置栈结构来保存走过的路
该方法与上面利用函数调用栈的实现思路相同。但是需要手动维护一个栈结构。如果经过某处时,发现该处可以落脚,再将该处的位置信息入栈,表示已经探索过该位置。
Path函数的实现思路如下:
(1)首先需要设置一个栈结构来保存走过的位置信息
(2)然后从入口点开始探索。先判断入口点是否能够落脚,如果不能落脚直接返回即可。
(3)如果入口点能落脚,就标记入口点,并将入口点的位置信息压入栈中表示走过该点
(4)取栈顶元素进行判断,如果栈为空,说明已经回溯结束,没有出口。否则判断栈顶元素是否为出口点,如果是出口点,直接打印返回即可
(5)如果栈顶元素不是出口点,就顺时针探测该栈顶元素的四周点。
(6)首先探测上面的点。如果上面的点能够落脚,将其标记并压入栈中。然后回到(4)。
(7)如果不能落脚,再分别顺时针探测右,下,左侧的点,探测方法与(6)相同
(8)如果四周的点都探测完了还没找到出口,就出栈栈顶元素,回到(4)。相当于回溯,继续探测上一个位置的四周点。
代码实现如下:
void PathStack(Maze* maze,Point entry)
{
if(maze == NULL)
{
return;
}
SeqStack stack;
InitSeqStack(&stack);
//1. 首先判断入口点能不能落脚,如果不能落脚,直接退出返回即可
if(CanStay(maze,entry) == 0)
{
return;
}
//2. 入口点能落脚,说明入口点可以走,然后对入口点进行标记,将入口点入栈
Mark(maze,entry);
SeqStackPush(&stack,entry);
//3. 判断入口点是否为出口点,如果满足出口点的条件,就说明找到了一条出口,直接退出即可
while(1)
{
Point cur;
int ret = SeqStackTop(&stack,&cur);
if(ret == -1)
{
//栈为空,说明回溯结束,没有出口
printf("没有出口\n");
return;
}
printf("(%d,%d)\n",cur.row,cur.col);
if(IsExit(cur,entry) == 1)
{
printf("找到了一个出口\n");
return;
}
//4. 如果不是出口,就顺时针探测入口点的四周点,将四周点作为新的当前点就行探索
//5. 如果新的当前点能够落脚,就进行标记并入栈,然后判断当前点是否为出口等等
Point up = cur;
up.row -= 1;
if(CanStay(maze,up) == 1)
{
Mark(maze,up);
SeqStackPush(&stack,up);
continue;
}
//6. 如果当前点不能落脚,就探测下一个四周点
Point right = cur;
right.col += 1;
if(CanStay(maze,right) == 1)
{
Mark(maze,right);
SeqStackPush(&stack,right);
continue;
}
Point down = cur;
down.row += 1;
if(CanStay(maze,down) == 1)
{
Mark(maze,down);
SeqStackPush(&stack,down);
continue;
}
Point left = cur;
left.col -= 1;
if(CanStay(maze,left) == 1)
{
Mark(maze,left);
SeqStackPush(&stack,left);
continue;
}
//6. 如果当前点能落脚,就将当前点入栈,并标记,然后判断当前点是否为出口
//7. 如果四周点都已经探索完,就将当前点出栈,探索其他路径
SeqStackPop(&stack);
}
} 其中,上述代码中的CanStay函数,Mark函数,IsExit函数与3中的实现相同。另外,有关上述代码中的栈及栈的相关操作间如下博客:https://blog.csdn.net/sandmm112/article/details/79860236
注意:在上述博客中顺序栈在实现时里面存放的时char类型的数据,而在本问题中,要存放的是结构体Point类型的变量,所以需要稍作修改
问题二:在多个出口中找到最短路径
迷宫地图如下图:
在上图中有多个出口,此时不仅需要找到出口,还需要找到通往出口的最短路径。
问题分析:
1. 首先要初始化迷宫地图,方法与上述初始化函数相同,只需将地图对应的状态信息改为上图所表示的即可。
2. 实现Path函数。
在该问题中,还是利用函数的调用栈来保存经过的位置信息。该函数的实现思路与问题一3中的思路类似。在本问题中,要求找到通往出口的最短路径。所以,在探索迷宫的过程中,需要将走过的位置信息保存下来。此时需要利用两个栈结构来分别实现保存当前路径的位置信息和最短路径的位置信息。每到一个出口,就比较当前路径和最短路径,如果当前路径比最短路径短,就将当前路径赋值给最短路径。然后在探索其他的出路,直到将所有的出口均探索完毕即可。
void PathShort(Maze* maze,Point entry)
{
if(maze == NULL)
{
//非法输入
return;
}
//因为要找最短路径,所以需要保存当前已经走过的路径和最短路径,
//如果当前路径比最短路径短,则将当前路径替换为最短路径
//所以需要维护两个栈,来保存当前路径走过的位置信息和最短路径中的位置信息
SeqStack cur_path;
SeqStack short_path;
InitSeqStack(&cur_path);
InitSeqStack(&short_path);
_PathShort(maze,entry,entry,&cur_path,&short_path);
PrintShortPath(&short_path,"打印最短路径");
} 回调函数的实现思路如下:
(1)从当前点开始,首先判断当前点能否落脚,如果不能落脚,则回溯退出当前函数的调用栈
(2)如果能落脚,就标记当前点表示走过该点,并将当前点的位置信息压入当前路径栈中
(3)判断当前点是否是出口,如果是出口,说明找到了一条出路
a)如果当前路径比最短路径短或者最短路径为空,就将当前路径赋值给最短路径
b)如果当前路径比最短路径长,就不做处理
然后,将当前位置从当前路径出栈,在进行回溯探索其他的路径
(4)如果当前点不是出口,就顺时针探索当前点的四周点
(5)探测完当前点的四周点后,就将当前点从当前路径中出栈,回溯探测其他的路径。
代码实现如下:
void _PathShort(Maze* maze,Point cur,Point entry,SeqStack* cur_path,SeqStack* short_path)
{
if(maze == NULL || cur_path == NULL || short_path == NULL)
{
//非法输入
return;
}
//1. 首先判断当前点能否落脚,如果当前点不能落脚,则回溯退出当前的调用栈
if(CanStay(maze,cur) == 0)
{
return;
}
//2. 如果能落脚,就标记当前点表示走过该点,并将该当前点入栈到当前路径中
Mark(maze,cur);
SeqStackPush(cur_path,cur);
//3. 判断当前点是否是出口,如果是出口点,说明找到了一个出口
if(IsExit(cur,entry) == 1)
{
printf("找到了一个出口\n");
// a)如果当前路径比最短路径短或最短路径为空,就将当前路径赋值给最短路径
if(short_path->size == 0 || cur_path->size < short_path->size)
{
PathCopy(cur_path,short_path);
}
// b)如果当前路径比最短路径长,最不做处理
// c)将当前点从当前路径中出栈,再进行回溯探测其他的路
SeqStackPop(cur_path);
return;
}
//4. 如果当前点不是出口,就顺时针探测当前点的四周点,将四周点作为新的当前点传给回调函数
Point up = cur;
up.row -= 1;
_PathShort(maze,up,entry,cur_path,short_path);
Point right = cur;
right.col += 1;
_PathShort(maze,right,entry,cur_path,short_path);
Point down = cur;
down.row += 1;
_PathShort(maze,down,entry,cur_path,short_path);
Point left = cur;
left.col -= 1;
_PathShort(maze,left,entry,cur_path,short_path);
//5. 探测完四周点后,就将当前点从当前路径中出栈,回溯探测其他的路径
SeqStackPop(cur_path);
return;
}
其中,赋值路径函数PathCopy的实现如下:
要将当前路径栈中所保存的的位置信息赋值给最短路径栈,有下列三种情况:
(1)最短路径栈中所容纳的位置数比当前路径栈中的位置多
(2)最短路径栈中所容纳的位置数比当前路径栈中的位置少
(3)最短路径栈中所容纳的位置数比当前路径栈中的位置相等
因为这两个栈结构是用顺序栈来实现的,而顺序栈又是通过动态申请内存来实现的,所以如果最短路径栈中的位置个数足够,也就是出现上述的(1)(3)情况,此时直接复制即可。如果出现上述的情况(2),说明动态申请的空间不够用了,此时,首先需要申请足够大的内存空间,再复制位置信息即可。
代码实现如下:
void PathCopy(SeqStack* from,SeqStack* to)
{
if(from == NULL || to == NULL)
{
//非法输入
return;
}
//1. from比to长
if(from->size > to->capacity)
{
Destory(to);
to->capacity = from->capacity;
to->size = from->size;
to->data = (SeqStackType*)malloc(to->capacity*sizeof(SeqStackType));
}
//2. from比to短
//3. from和to相等
//此时不做处理
//赋值位置信息
int i = 0;
for(;i < from->size;++i)
{
to->data[i] = from->data[i];
}
return;
} 运行完上述代码后,最短路径信息已经保存在栈short_path中,只需将其打印出来即可。
问题三:在带环多出口中找最短路径
假设迷宫地图如下:
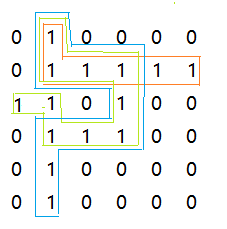
如果继续同时用问题二中的方法,迷宫的探测路径如下:
上图中三种颜色框起来的即为用上述算法探测出的路径。发现此时没有找到真正的最短路径:(0,1)->(1,1)->(2,1)->(2,0)。那是因为在回溯到点(1,1)处时,本想继续往点(2,1)处走,但在之前的探索绿色框框起来的路径已经将该点探测过并且将其标记为2,所以再次进行探测时,发现该处标记为2,说明不能走。所以就不能继续往下探测了。所以实际最短路径并没有找到。
所以,上述的算法不适用于本问题。
该问题的实现思路如下:大体思路与问题二中的思路相同。只是在判断落脚点和标记走过的路时需要作如下修改:
标记函数思路:
(1)初始时,如果入口点可以落脚,就将入口点标记为2,这里的2表示到该点时:走过的步数加1。
(2)之后,没走过一处,将该点标记为:走该点的步数加1。如走到(1,1)点时,此时走过了两步,所以将该点标记为3.
判断落脚点函数思路:
(1)如果当前位置在地图之外,则不能落脚
(2)如果当前位置处的值为0,说明是墙,也不能走
(3)如果当前位置处的值为1,说明是路且没有被探测过,说明可以落脚
(4)如果当前位置已经被标记过,且重新走到该处的步数比已经标记的步数少,说明可以找到更短的路来走到该处,此时也可以落脚
(5)如果,当前位置已经被标记过,且重新走到该处的步数比已经标记的步数多,说明此时肯定最短路径,所以不必延当前路径继续探测了,所以不能落脚。
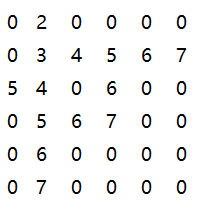
根据上述思路,在上图中,因为蓝色框的路径先被探测,所以走到(2,1)处需要9步,所以将该位置标记为10。等到图上三条路径已经探测完毕回溯到点(1,1)时,发现重新到达点(2,1)的步数可以缩短至3((0,1)->(1,1)->(2,1)),所以此时(2,1)处可以重新落脚,这样便可以接着往下探测,这样便可以找到最短路径。
所以,对带环迷宫地图,用上述标记方法可以得到如下的各条路径:
标记函数的实现:
因为标记当前点时,还需要用到当前点的先前点处的值,所以还需要将先前点的位置信息作为参数传入。同时因为入口点没有先前点,所以手动设置一个入口点的向前点,如(-1,-1),再根据先前点是否为(-1,-1)来判断是对入口点标记还是对其他点进行标记。根据上述的思路,代码实现如下:
void MarkWithCycle(Maze* maze,Point cur,Point pre)
{
//如果最初是对入口点标记,直接将入口点标记为2即可
if(pre.row == -1 && pre.col == -1)
{
maze->map[cur.row][cur.col] = 2;
return;
}
//如果是对其他点进行标记,则将当前点的值设置为入口点的值加1即可
int pre_value = maze->map[pre.row][pre.col];
maze->map[cur.row][cur.col] = pre_value + 1;
return;
}判断落脚点的函数实现:
因为在判断当前点能否落脚时,还需要根据先前点处的值来给出到达当前位置所需要的步数,所以还需要将先前点的位置信息作为参数传入。同时,因为入口点没有先前点,所以手动设置一个入口点的先前点即可。在对入口点进行落脚点判断时,进行特殊的判断即可。
代码实现如下:
//判断带环迷宫当前点能否落脚
int CanStayWithCycle(Maze* maze,Point cur,Point pre)
{
//如果当前点在地图之外,就不能落脚
if(cur.row < 0 || cur.row >= ROW || cur.col < 0 || cur.col >= COL)
{
return 0;
}
int cur_value = maze->map[cur.row][cur.col];
//如果当点位置是墙,则不能落脚
if(cur_value == 0)
{
return 0;
}
//如果当前位置是没有走过的路
if(cur_value == 1)
{
return 1;
}
//如果当前位置已经探索过,并且它的先前点的值加1小于当前点的值,就可以落脚,否则不能落脚
//如果是入口点,那它的先前点位置坐标是非法值,不能取值。此时入口点有三种状态
//a) 在地图之外
//b) 是墙
//c) 是路
//而以上三种情况在上面已经判读过,所以这里不需要在重复判断,也就是说,
//如果使入口点,就不会走到这一步,一定属于上面三种情况,而提前返回。能走到这一步,说明当前点一定不是入口点
//所以,就不用考虑先前点的位置非法的问题
int pre_value = maze->map[pre.row][pre.col];
if(pre_value + 1 < cur_value)
{
return 1;
}
else
{
return 0;
}
}
在本问题中,递归函数的实现思路与问题二中的思路相同:
void _PathShortWithCycle(Maze* maze,Point cur,Point entry,Point pre,SeqStack* cur_path,SeqStack* short_path)
{
if(maze == NULL || cur_path == NULL || short_path == NULL)
{
//非法输入
return;
}
//1. 判断当前点能否落脚,如果不能落脚,直接回溯出函数的调用栈
if(CanStayWithCycle(maze,cur,pre) == 0)
{
return;
}
//2. 如果能落脚,就标记当前点表示走过该点,并将该当前点入栈到当前路径中
MarkWithCycle(maze,cur,pre);
SeqStackPush(cur_path,cur);
//3. 判断当前点是否是出口,如果是出口
if(IsExit(cur,entry) == 1)
{
printf("找到了一个出口\n");
// a) 如果当前路径比最短路径短或最短路径为空,就将当前路径赋值给最短路径
if(short_path->size == 0 || cur_path->size < short_path->size)
{
PathCopy(cur_path,short_path);
}
// b) 如果当前路径比最短路径长,就不做处理
// c) 然后将当前点从当前路径出栈,再回溯探索其他的路
SeqStackPop(cur_path);
return;
//4. 如果不是出口,就顺时针探测当前点的四周点
Point up = cur;
up.row -= 1;
_PathShortWithCycle(maze,up,entry,cur,cur_path,short_path);
Point right = cur;
right.col += 1;
_PathShortWithCycle(maze,right,entry,cur,cur_path,short_path);
Point down = cur;
down.row += 1;
_PathShortWithCycle(maze,down,entry,cur,cur_path,short_path);
Point left = cur;
left.col -= 1;
_PathShortWithCycle(maze,left,entry,cur,cur_path,short_path);
//5. 如果四周点都已经探索完,就将当前点从当前路径中出栈,然后回溯探测其他的路
SeqStackPop(cur_path);
return;
}}
_Path函数:
void PathShortWithCycle(Maze* maze,Point entry)
{
if(maze == NULL)
{
//非法输入
return;
}
SeqStack cur_path;
SeqStack short_path;
InitSeqStack(&cur_path);
InitSeqStack(&short_path);
Point pre = {-1,-1};
_PathShortWithCycle(maze,entry,entry,pre,&cur_path,&short_path);
PrintShortPath(&short_path,"打印最短路径");
return;
}