人工智能原理笔记------知识表示方法

知识表示

对知识的描述，即用一组符号把知识编码成计算机可以接受的某种结构。其表示方法不唯一。

知识表示方法

非结构化方法

谓词逻辑表示法

这里我们主要讨论一阶谓词逻辑表示法，其是一种基于数理逻辑的表示方法，其中数理逻辑可分为一阶经典逻辑与非一阶经典逻辑。

1. 一阶经典逻辑：一阶经典命题逻辑，一阶经典谓词逻辑
2. 非一阶经典逻辑：指除经典逻辑以外的那些逻辑，例如：二阶逻辑，多值逻辑，模糊逻辑等。

命题

断言：一个陈述句称为一个断言。
命题：具有真假意义的断言称为命题。
即判断，用于表述客观世界的、可以分辨真假且非真即假的的陈述句。

真值

真T：表示命题的意义为真
假 F：表示命题的意义为假
陈述句是否能分辨真假与是否知晓其真值没有关系。(反例：我们不知道这个陈述句的正值，所以其真值无法判断 )

论域（个体域）

由所讨论对象的全体构成的集合。亦称为个体域。
个体：论域中的元素。

谓词

在谓词逻辑中命题是用形如 P(x1,x2,…,xn) 的谓词来表示，其中：
谓词名：是命题的谓语，表示个体的性质、状态或个体之间的关系(离散中的谓词常量或谓词变量)
个体：是命题的主语，表示独立存在的事物或概念

x1,x2,…,xn构成论域，P(x1,x2,…,xn)为n元谓词或n元简单命题函数，这里的简单指的是这里只有一个谓词。多个简单命题函数运算后可以得到复合命题函数。简单命题函数与复合命题函数统称命题函数。

函数

设D是个体域，f：Dn→D是一个映射， 则称f是D上的一个n元函数，记作 f(x1,x2,…,xn)

特别注意：函数与命题的区别，首先两者虽然都是映射关系，但是命题映射的结果只有真假，而函数映射的结果是一个个体域。换一句描述就是谓词得到的是真值（真T，假F），函数得到的是实际的个体元素（函数的值）。

在谓词逻辑中，谓词可独立存在，函数只能作为谓词的个体，由谓词与函数（映射得到元素）构成命题。
上文中的简单命题函数是离散中的概念，指的是函数的映射值为真或假。

谓词逻辑组成

命题的谓词表示：
举例：Friend(A,Brother(B))
A与B的哥哥是朋友
这里的Friend是谓词符号，Brother(X)是函数（函数符号），表示X的哥哥这个映射关系。谓词Friend(x1,x2)表示x1与x2的朋友关系，x1，x2是变量符号，变量具体到实际的A与B时，A与B为常量符号。

连接词

合取(与) ^：A ^ B 为真，当且仅当A、B同时为真。

析取（或）v：A v B为假，当且仅当A、B同时为假

否定（非）~ : ~ A为真，当且仅当A为假(符号表示应该为笔画中的横折而不是~)

蕴涵 =>：A => B为假，当且仅当A为真，B为假(符号表示应该为右箭头而不是 => )
等价式为 ~ A v B
除此之外在离散数学的定义中还有许多其他的连接词，但是都可以由合取，析取与否定生成，在此不再赘述。

约束量词

全称量词：表达变量x在其论域内的所有可能取值。强调“所有的”、“任一个”。(符号是一个倒立的A)
存在量词：表达变量x在其论域内，存在着、有一个、或至少有一个取值。(符号是一个反写的E)。

谓词公式

项：个体常量、个体变量（基本的项）
若t1,t2,…,tn是项，f是n元函数，则f(t1,t2,…,tn)是项；
由以上两个进行生成的表达式也是项。
个体常量、个体变量和函数统称为项。

原子谓词公式：若t1,t2,…,tn是项，P是谓词，则称P(t1,t2,…,tn)为原子谓词公式。

相关规则：

1. 原子公式是谓词公式。
2. 若A是谓词公式，其否定也是。
3. 若A,B是谓词公式，其进行的合取与析取运算也是。
4. 若A是谓词公式，x是项，对x的约束量词表达式产生的也是谓词公式。

量词的辖域
量词的约束范围，即指位于量词后面的单个谓词或者用括弧括起来的合式公式。例：

约束变元：受到量词约束的变元，即辖域内与量词中同名的变元称为约束变元
自由变元：不受约束的变元称为自由变元
例·：

变元的换名：谓词公式中的变元可以换名。要保持变量的论域不变。
约束条件：（存在量词约束的变量换名也一样）

1. 对约束变元，必须把同名的约束变元都统一换成另外一个相同的名字，且不能与辖域内的自由变元同名。
   
2. 对辖域内的自由变元，不能改成与约束变元相同的名字。
   

谓词公式真值表：取出公式中所有单个谓词，按所有可能的取值组合，再按连接词和量词的定义给出合适公式的真值。例：

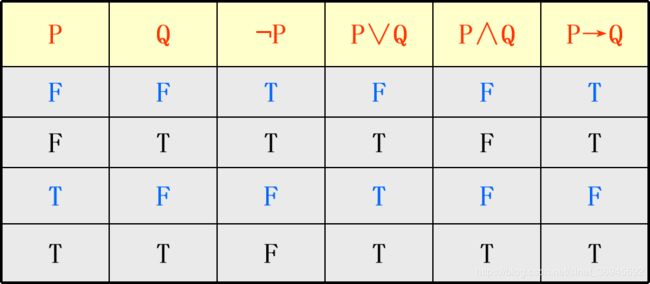
等价公式：



这里的量词转换中，对任意往往使用析取来代替描述，对存在则使用合取来描述。

谓词逻辑表示步骤

先根据要表示的知识定义谓词，再用连词、量词把这些谓词连接起来。

产生式表示法

产生式规则

形如下列的语句叫做一条产生式规则

1. P→Q
2. IF P THEN Q
3. 如果 P，那么 Q

P叫做：前件、前项、左边。给出了该产生式可否使用的前提条件
Q叫做：后件、后项、右边。指出当前提P满足时，应该推导出的结论或应该执行的动作。

产生式的含义和作用

含义：如果前提P满足，则可推出结论Q或执行Q所规定的操作
作用：产生式规则用来表示问题领域的一般知识

与逻辑蕴涵的比较

1. 逻辑规则的两边只能是命题或谓词，产生式可以是命题和谓词，也可以是其他符号串；
2. 逻辑规则要满足真值表，即前后件最终只能为T或F。产生式前后件都可以是任意类型的值，产生式规则右边可能是动作，甚至是复杂的过程语句；
3. 产生式可以处理不确定性，逻辑规则只能用于确定推理；
4. 逻辑规则可以视为产生式规则，反之不然；
5. 形式相同，产生式应用范围更广；

与条件语句的比较

1. 前项结构不同，产生式的前项可以是一个复杂的的结构，其值不一定为逻辑类型。
2. 控制流程不同：产生式系统中满足前提条件的规则被激活后，不一定被立即执行，能否执行将取决于冲突消解策略。

巴克斯范式描述（BNF）

以美国人巴科斯(Backus)和丹麦人诺尔(Naur)的名字命名的一种形式化的语法表示方法，用来描述语法的一种形式体系，是一种典型的元语言。又称巴科斯-诺尔形式(Backus-Naur form)。它不仅能严格地表示语法规则，而且所描述的语法是与上下文无关的。
BNF表示语法规则的方式为：非终结符用尖括号括起。每条规则的左部是一个非终结符，右部是由非终结符和终结符组成的一个符号串，中间一般以“：：=”分开。具有相同左部的规则可以共用一个左部，各右部之间以直竖“|”隔开。

1. 尖括号( < > )内包含的为必选项
2. 方括号( [ ] )内包含的为可选项
3. 竖线( | )表示在其左右两边任选一项，相当于"OR"的意思。
4. ::= 是“被定义为”的意思。

产生式的BNF描述
<规则> ::= <前提> -> <结论>
<前提> ::= <简单条件> | <复合条件>
<结论> ::= <事实> | <动作>
<复合条件> ::= <简单条件> AND <简单条件> [( AND <简单条件> … )] | <简单条件> OR <简单条件> [( OR <简单条件> … )]
<动作> ::= <动作名> | [( <变元> … )]

结构化方法

语义网络表示法

语义网络

语义网络是知识的一种结构化有向图表示方法。具有与产生式相同的表示能力。

结点（节点）：代表实体，表示各种事物、概念、情况、属性、状态、事件、动作等
弧（有向边）：关系

语义基元

语义网络中最基本的语义单元称为语义基元，可用三元组表示为： （结点1，弧，结点2）

基本网络单元

指一个语义基元对应的有向图。

基本语义关系

1.实例关系： ISA
体现的是“具体与抽象”的概念，含义为“是一个”，表示一个事物是另一个事物的一个实例（类与对象）。

2.分类关系： AKO
亦称泛化关系，体现的是“子类与超类”的概念，含义为“是一种”，表示一个事物是另一个事物的一种类型。

3.成员关系： A-Member-of
体现的是“个体与集体”的关系，含义为“是一员”，表示一个事物是另一个事物的一个成员。

4.聚集(聚类、包含)关系
表达整体与其组成部分的关系。

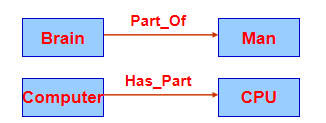
聚类关系一般不具备属性的继承性

5.属性关系
指事物和其属性之间的关系,一个结点是另一个结点的属性值。

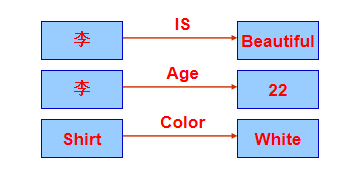
6.拥有关系——Have， Own

7.时间关系——Before、After、At等
指不同事件在其发生时间方面的先后次序关系。

8.位置关系——Located_on (_at, _inside, _outside等)

9.相似、相近关系——Similar-to, Near-to

10.推论关系——Infer

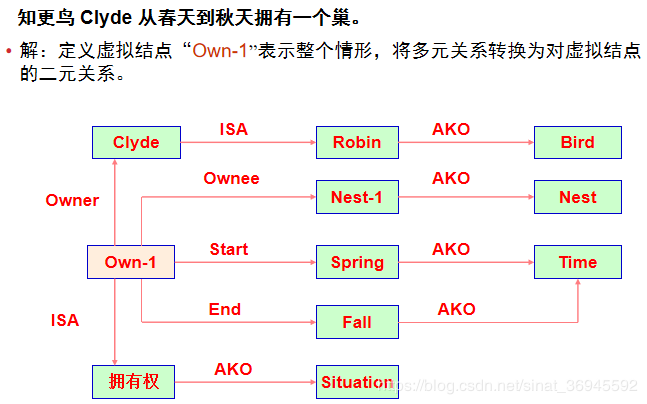
多元语义处理

引入情形、事件、动作、概念等虚拟结点，将复杂的多元关系转换为多个二元关系，以表达复杂的知识。
此虚拟结点代表整个场景。

框架表示法

框架是一种描述所讨论对象（事物、事件、概念等）属性和行为的数据结构。

框架名

每个框架都有一个框架名，唯一标识一个框架。

槽（Slot）、槽名、槽值

一个框架由若干个槽构成，每个槽都有槽名；
一个槽用于说明框架某一方面的属性；
属性的值即为槽值。

侧面（Facet）、侧面名、侧面值

一个槽有可能划分为若干个侧面，具有相应的侧面名；
一个槽可能含有若干细分属性，一个侧面用来说明其中的一个属性；
属性的值即为侧面值。

约束条件

用来约束、限制槽值、侧面值的填写。一般不单独列出，而包含在值的填写约束中。

框架与框架实例

框架：是人们认识事物的一种通用的数据结构形式。即当新情况发生时，人们只要把新的数据加入到该通用数据结构（类）中便可形成一个具体的实体(对象)，这样的通用数据结构就称为框架。
实例框架：对于一个框架，当人们把观察或认识到的具体细节填入后，就得到了该框架的一个具体实例，框架的这种具体实例被称为实例框架。

框架的继承

通过AKO、ISA槽从上层框架往下层框架，或从框架向框架实例进行继承。

框架网络（框架系统）

框架是知识的基本单位，把一组有关的框架连结起来便可形成一个框架网络（框架系统）。
连接手段：

1. 继承 — 框架的纵向联系
2. 用另一框架填写槽值或侧面值 — 框架的横向联系

例：