个人笔记——PointNet初学

PointNet是斯坦福大学发表在2017年CVPR上的一篇处理点云数据的论文。相较于之前其他处理点云数据的论文，其最大的不同是，对于点云数据，会直接进行处理，而非将点云数据进行格式化处理，从而避免了将点云数据格式化后，产生的unnecessarily voluminous以及像素点失真的问题。从这一点上来说，PointNet具有极其重要的意义。

从传统思路来讲，通过将点云数据转换成3D像素数据后，可以将3D像素数据像处理2维图像一样，进行卷积，权值共享等，而显而易见，对于无序的一些点的集合，是无法直接像和处理2D数据一样进行处理，在原文中，当直接使用点云数据不加处理时，作者提出了以下3个可能产生的问题，以及主要就这3个问题，进行的网络结构的设计以及相关的证明和实验：

1、输入无序性问题

从数据结构的角度来讲，点云数据知识一组无序的向量集合，若不考虑其他诸如颜色等因素，只考虑点的坐标，则点云数据只是一组n * 3的点集合。那么当对这n个点进行不同顺序的读入时，无论是图像分类抑或是部分分割，都必须输出相同的结果，在2D图像中，因为点的位置是固定的，所以不存在这样的问题，但是在点云数据中，点的输入组合中共有n！种，所以必须进行处理。

在论文中，处理的方式也比较简单，使用了最大池化，在对n个点进行卷积等操作后，生成n * 1024维的矩阵，1024维的1024个整体特征，对于每个维度，求其最大值，即解决了输入无序性的问题。此处可举例有max（a,b,c,d,e,f,g） =  max (a,d,b,e,c,f,g) = ...

在论文的4.3部分，作者就使用最大池化进行证明，当特征维数足够大时，最大池化可以对模拟论文中所述的任意对称函数f，同时在此基础上论述了模型的稳定性。对于任意数据集S，Cs表示critical set，Ns表示upper-bound set，即对于相同全局特征f(s)，所可能的最大点云集，此时有f(Ns) = f(S), 故而当添加的点属于Ns - S时，对于整体点云特征并无影响，故而满足稳重所述的robust to small pertubation of input points。此处其实与svm中的支持向量有点类似，以及凸包中，被包住的点。最终作者的结论是网络学习到了概括形状的关键点，即点云的骨架。

2、点与点之间的相关性

在分类问题中，此问题其实不是特别重要，在分类中，只要处理出全局特征，通过对全局特征进行mlp或者用svm分类等，即可得到最终答案，但是在part segmentation 以及 scene semantic parsing中，此问题就显得极其重要。

论文中进行处理时，通过将提取出的全局特征以及点特征结合，得到n * 1088（64 + 1024）的特征矩阵，然后在此矩阵的居处上，重新提取每个点的特征，得到包含局部及全局特征的点信息。

3、旋转不变性

对于一个3维图像，当我们进行例如旋转、上移等操作时，不论是目标分类还是部分分割，都应保证其结果不变。

而解决此问题的方法是通过添加一个T-Net，对原始点矩阵进行仿射变换。相当于在数据预处理阶段直接进行处理，保证其后的结果不变性。训练的T-Net是数据依赖的。同时，在其后的点的特征空间，作者也同样加了一个T-Net进行处理，但相较于前一个3 * 3变换矩阵，此变换矩阵为64 * 64 = 4096，由于变换矩阵过大，通过添加正则项，使变换矩阵近似于正交矩阵，此时所需要的参数将大大减少。

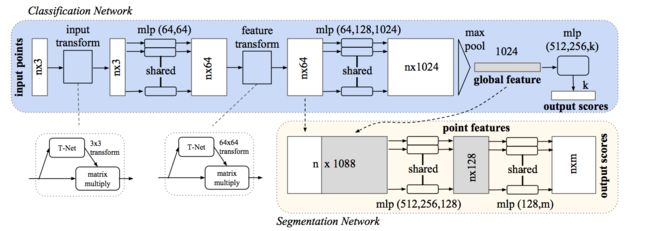
最后对图中的网络结构结合具体代码进行分析：

在输入点云数据后，首先进行T-Net进行仿射变换，具体表现为乘以3*3的转换矩阵，其后通过卷积层进行特征提取，根据代码得知，mlp(64,64)的两层卷积层的卷积核数量都为64，其中第一层卷积的卷积核大小为1 * 3，第二层为1 * 1的核。而后进行相同的feature transform，在下一个mlp(64,128,1024)中，卷积核的大小都为1 * 1。在池化层后，分别连接三个全连接层，输出节点个数依次为512、256、k，最终使用softmax函数得到结果。