BP——反向传播算法公式推导及代码
BP——反向传播算法公式推导及代码
- 人工神经网络的结构
- 前向传播
- 激活函数
- 反向传播
- 梯度下降
- 具体计算过程
本文主要参考吴恩达和李宏毅的深度学习视频,然后自己做的笔记
反向传播计算部分参考李宏毅的视频讲解,要是有童鞋也对反向传播这一部分的计算不那么清明,可以考虑选择留下来看看我的笔记,也可以移步李宏毅大神的视频讲解
人工神经网络的结构
(注:Markdown敲公式对我来说太困难,后面的公式都用图片的形式展示)
神经网络的结构包括:输入层(input layer)、隐藏层(hidden layer)、输出层(output layer)。如下图所示:
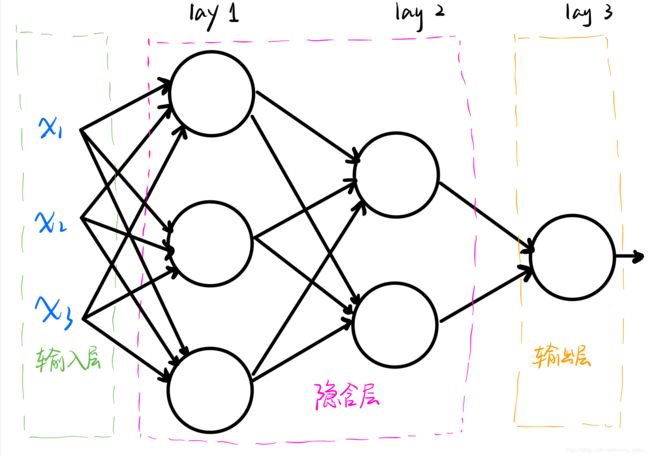
当然,隐含层可以有无数层,这里我只画了两层。
输入层输入的数据是训练样本(x1,x2,…,xn,y),训练样本中的x1到xn表示输入的特征值,而y则表示咱们希望输出的预期值。
隐含层将会进行一系列的计算来缩小训练样本的估计值y’与预期值y之间的误差。
输出层则会输出训练后得到的估计值y’。
前向传播
为了后面的表示方便,我们这里先约定一下每个神经元的表示方法。
aj[l][i]:第i个样本的第l层上第j个神经元的输入,且有 a[0] = x 。
z:中间变量
J:代价函数
g():激活函数
前向传播主要完成两个任务:
- 计算每一个神经元的激活值a;
- 是计算最后的代价函数J(y’, y)(如果我们这里只有一个输入样本的话,那么应该叫做损失函数)。
即将用到的公式有(这里就以上面给出的人工神经网络结构为例子,即一个样本的表示形式):

我们定义
前向传播的计算流程:
- 输入的准备工作:a[0]、w[1]、b[1]都排排坐,下面准备吃果果啦~
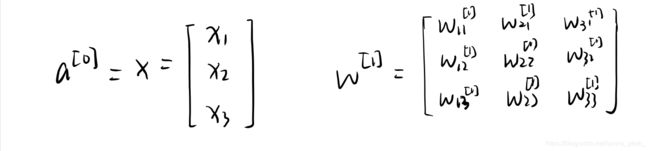
- 求出a[1]
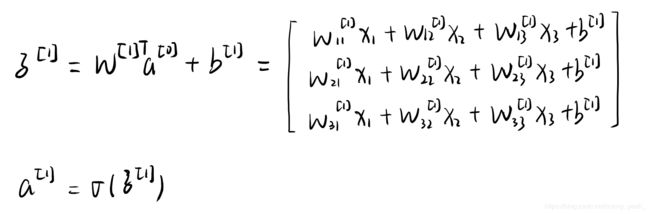
根据【人工神经网络结构图】可知,咱们的三个输入都连接到了三个神经元上,每个神经元都要有一个输出,因此咱们最后求得的a[1]也是一个3*1的向量。
咱们将上面的式子扔到神经网络中表示:
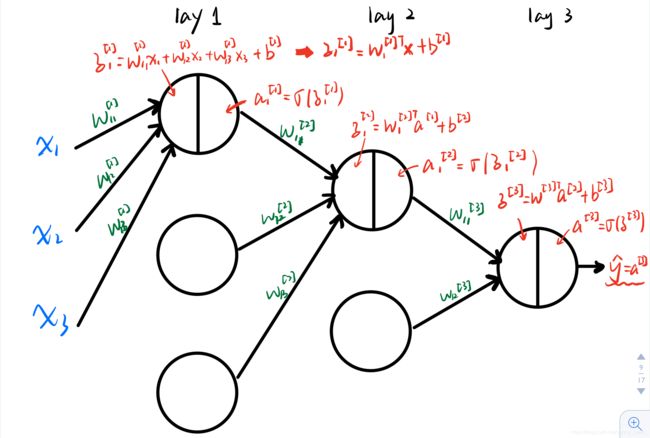
看到没有,每一个神经元都要进行一次z和a的计算,一直传到输出层,输出层求得的a就是咱们样本的估计值!
在python中表示求解z、a的式子为:
z = np.dot(w.T, x)+b
a = sigmoid(z) #这里我采用sigmoid()函数作为激活函数,这个函数主要是用来作二分类
- 损失函数J(y’, y)在python中的表示:
损失函数:求解单个样本的误差
代价函数:求解多个样本的误差
cost = -y * np.log(y') - (1 - y) * np.log(1 - y') #这里只是单个样本的损失函数,如果咱们有m个样本的话就需要将这m个样本的损失值全部加起来再除以m求得这m个样本的代价函数。
激活函数
激活函数的作用:加入非线性因素,解决线性不可分问题。(比如说,现在给你一个得用歪七扭八的线来划分两个区域,你用直线肯定是不可能把他俩完美的分开的,但是加入非线性因素以后,你就可以拟合出一条近乎完美的线来划分这两个区域啦~)
激活函数有很多种,咱在上面使用的是用于二分类的一种常用的激活函数,一般用在输出层。(不同层可以使用不同的激活函数,还有一点很重要的是:激活函数得是可微的!因为咱们在反向传播阶段得对激活函数求导!)
各种激活函数详情请咨询:千奇百怪的激活函数 来源:wikipedia
反向传播
老规矩,先约定一波:
dw: J对w求偏导
db: J对b求偏导
dz: J对z求偏导
da: J对a求偏导
步骤:
- 求解dw, db
- 更新w, b
方法:梯度下降
小工具:链式求导
咱们在计算时一定一定会用到的四个公式:
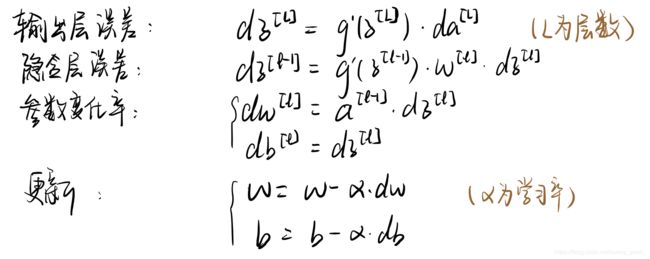
现在看不太明白这几个公式没有关系,咱们先往后走,看看具体是怎么计算的,一会再看这些公式心就明朗啦~ 加油加油,马上就完了!
梯度下降
咱们要清楚,方向传播的目的就是为了找到一个最好的w和b,让咱们的损失达到最小,让咱们的结果无限逼近最优解。那么为了让咱们这个值达到最优,咱们就要采用梯度下降的方法来不断优化这个值。当然,学习率的选择也是非常重要的。不然就可能出现两种不太招人待见的情况:1.要训练贼多次才能到达最优解;2.始终到不了最优解。
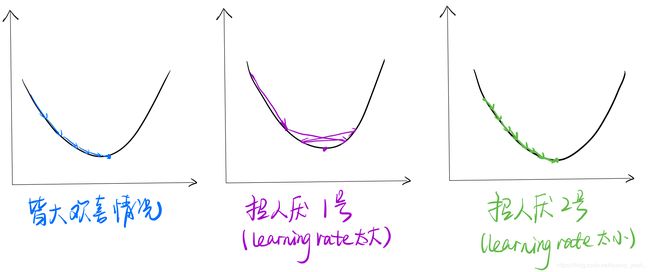
箭头所指的方向就是梯度下降的方向。
具体计算过程
step1. 计算隐藏层误差(这里以第一个神经元为例)
思路:要求解dw[1]和db[1],先要求解出dz[1],要求dz[1],那么先要知道da[1]。因此咱们求解的过程就是da—>dz—>dw,db
过程如下:

可以看到上面的求解过程就是一个链式求导过程。一层一层的剥开,一层一层的求解。
step2. 计算输出层误差
输出层误差的求解过程中间只有一个da[L]这个中间变量。这个就留给大家自己写啦!(其实我最开始的地方都已经给出了)
step3. 咱们都知道每一层的dw和db是如何得到的了,现在要做的就是更新w和b了!还是用上面更新的那个公式来求解!这里我也不重复写了~
完结了~
咱们在实现过程中实际上也是不断迭代求解w和b来训练整个网络结构,使得整个网络的损失达到最小!
下面是大家最喜欢的部分!不贴代码的博客不是好博客!
import math
import random
import string
random.seed(0)
# calculate a random number where: a <= rand < b
def rand(a, b):
return (b - a) * random.random() + a
# Make a matrix (we could use NumPy to speed this up)
def makeMatrix(I, J, fill=0.0):
m = []
for i in range(I):
m.append([fill] * J)
return m
# our sigmoid function, tanh is a little nicer than the standard 1/(1+e^-x)
def sigmoid(x):
return math.tanh(x)
# derivative of our sigmoid function, in terms of the output (i.e. y)-derivative of tanh
def dsigmoid(y):
return 1.0 - y ** 2
class CBPNNClass:
def __init__(self, ni, nh, no):
# number of input, hidden, and output nodes
self.ni = ni + 1 # +1 for bias node
self.nh = nh
self.no = no
# activations for nodes
self.ai = [1.0] * self.ni
self.ah = [1.0] * self.nh
self.ao = [1.0] * self.no
# create weights
self.wi = makeMatrix(self.ni, self.nh)
self.wo = makeMatrix(self.nh, self.no)
# set them to random vaules
for i in range(self.ni):
for j in range(self.nh):
self.wi[i][j] = rand(-0.2, 0.2)
for j in range(self.nh):
for k in range(self.no):
self.wo[j][k] = rand(-2.0, 2.0)
# last change in weights for momentum
self.ci = makeMatrix(self.ni, self.nh)
self.co = makeMatrix(self.nh, self.no)
def update(self, inputs):
if len(inputs) != self.ni - 1:
raise ValueError('wrong number of inputs')
# input activations
for i in range(self.ni - 1):
# self.ai[i] = sigmoid(inputs[i])
self.ai[i] = inputs[i]
# hidden activations
for j in range(self.nh):
sum = 0.0
for i in range(self.ni):
sum = sum + self.ai[i] * self.wi[i][j]
self.ah[j] = sigmoid(sum)
# output activations
for k in range(self.no):
sum = 0.0
for j in range(self.nh):
sum = sum + self.ah[j] * self.wo[j][k]
self.ao[k] = sigmoid(sum)
return self.ao[:]
def backPropagate(self, targets, N, M):
if len(targets) != self.no:
raise ValueError('wrong number of target values')
# calculate error terms for output
output_deltas = [0.0] * self.no
for k in range(self.no):
error = targets[k] - self.ao[k]
output_deltas[k] = dsigmoid(self.ao[k]) * error
# calculate error terms for hidden
hidden_deltas = [0.0] * self.nh
for j in range(self.nh):
error = 0.0
for k in range(self.no):
error = error + output_deltas[k] * self.wo[j][k]
hidden_deltas[j] = dsigmoid(self.ah[j]) * error
# update output weights
for j in range(self.nh):
for k in range(self.no):
change = output_deltas[k] * self.ah[j]
self.wo[j][k] = self.wo[j][k] + N * change + M * self.co[j][k]
self.co[j][k] = change
# print N*change, M*self.co[j][k]
# update input weights
for i in range(self.ni):
for j in range(self.nh):
change = hidden_deltas[j] * self.ai[i]
self.wi[i][j] = self.wi[i][j] + N * change + M * self.ci[i][j]
self.ci[i][j] = change
# calculate error
error = 0.0
for k in range(len(targets)):
error = error + 0.5 * (targets[k] - self.ao[k]) ** 2
return error
def test(self, patterns):
for p in patterns:
print(p[0], '->', self.update(p[0]))
def weights(self):
print('Input weights:')
for i in range(self.ni):
print(self.wi[i])
print()
print('Output weights:')
for j in range(self.nh):
print(self.wo[j])
def train(self, patterns, iterations=1000, N=0.5, M=0.1):
# N: learning rate
# M: momentum factor
for i in range(iterations):
error = 0.0
for p in patterns:
inputs = p[0]
targets = p[1]
self.update(inputs)
error = error + self.backPropagate(targets, N, M)
if i % 100 == 0:
print('error %-.5f' % error)
def demo():
# Teach network XOR function
pat = [
[[0, 0], [0]],
[[0, 1], [1]],
[[1, 0], [1]],
[[1, 1], [0]]
]
# create a network with two input, two hidden, and one output nodes
n = CBPNNClass(2, 2, 1)
# train it with some patterns
n.train(pat)
# test it
n.test(pat)
if __name__ == '__main__':
demo()
代码来源:Andrew Ng的课程!这里并没有使用tensorflow框架,所以很多函数都是自己写的,大家可以将在这个代码上进行改写~